一个认为一切根源都是“自己不够强”的INTJ

个人主页：用哲学编程-CSDN博客
专栏：每日一题——举一反三
Python编程学习
Python内置函数

Python-3.12.0文档解读

目录

我的写法

代码优点

代码缺点

时间复杂度

空间复杂度

代码改进建议

我要更强

哲学和编程思想

KISS原则（Keep It Simple, Stupid）：

DRY原则（Don't Repeat Yourself）：

抽象化：

模块化编程：

优化算法和数据结构：

可读性和可维护性：

测试和调试：

举一反三

保持代码简洁：

避免重复代码：

抽象化：

模块化编程：

优化算法和数据结构：

提高可读性和可维护性：

测试和调试：

---

题目链接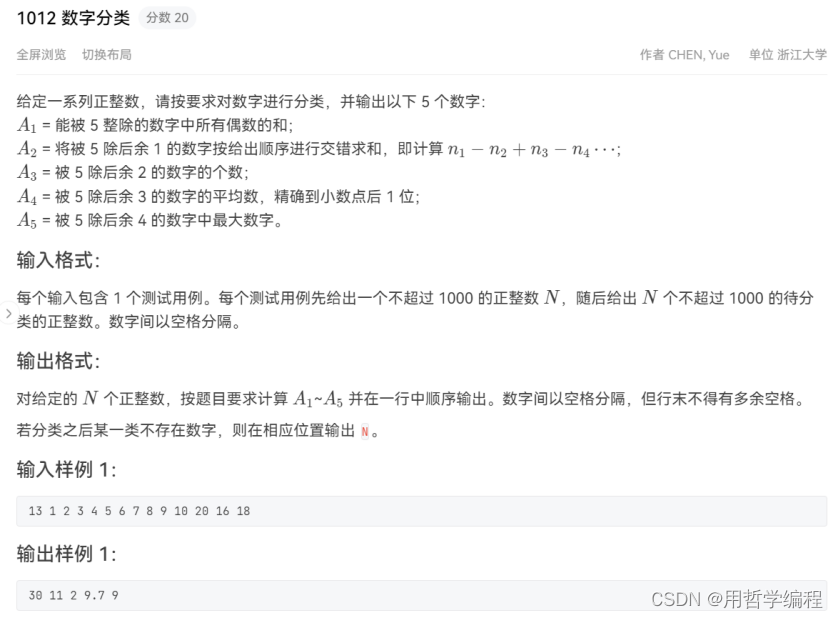

我的写法

# 从输入中读取数字，并将其转换为整数列表
nums = list(map(int, input().split()))

# N 是第一个元素，表示后面有多少个数
N = nums[0]

# 存储后面的 N 个数
nums = nums[1:]

# 初始化 5 个结果变量，分别对应 A1, A2, A3, A4, A5
A1 = A2 = A3 = A4 = A5 = 0

# 标志变量，用于记录是否存在符合条件的 A2 的数字
is_A2_no_N = False

# A2 的加减标志，初始化为 1，表示第一次遇到的数加，第二次减，依此类推
A2_flag = 1

# A4 的计数器，记录符合条件的数字的个数，用于计算平均值
A4_count = 0

# 遍历 N 个数，进行分类和求值
for num in nums:
    # 如果数字是 5 的倍数且是偶数，累加到 A1
    if num % 5 == 0 and num % 2 == 0:
        A1 += num
    # 如果数字除以 5 余 1，根据标志位进行加减运算，累加到 A2
    elif num % 5 == 1:
        is_A2_no_N = True
        A2 += A2_flag * num
        A2_flag *= -1  # 反转标志位
    # 如果数字除以 5 余 2，计数累加到 A3
    elif num % 5 == 2:
        A3 += 1
    # 如果数字除以 5 余 3，累加到 A4，并计数
    elif num % 5 == 3:
        A4 += num
        A4_count += 1
    # 如果数字除以 5 余 4，更新 A5 为最大值
    elif num % 5 == 4 and A5 < num:
        A5 = num

# 如果 A4 有符合条件的数字，计算其平均值
if A4_count:
    A4 = A4 / A4_count

# 将结果存储在列表中
results = [A1, A2, A3, A4, A5]

# 遍历结果列表，处理输出
for i in range(5):
    if results[i] == 0:
        # 如果结果为 0，特殊处理 A2，如果存在符合条件的数字，则不输出 'N'
        if i == 1 and is_A2_no_N:
            continue
        # 否则输出 'N'
        results[i] = 'N'
    else:
        # 如果是 A4，格式化输出为一位小数
        if i == 3:
            results[i] = f"{results[i]:.1f}"

# 打印最终结果
print(*results)

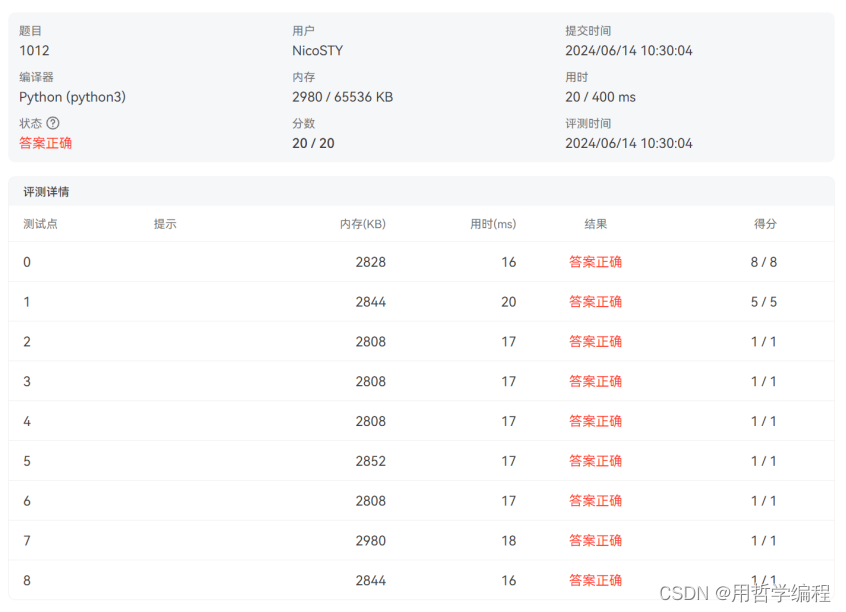
这段代码的目的是根据输入的一系列整数，分别计算并输出五个特定的结果（A1, A2, A3, A4, A5），这些结果根据数字对5的不同余数来分类计算。以下是详细的点评及复杂度分析：

代码优点

1. 逻辑清晰：代码逻辑清晰地处理了不同的余数情况，分别对结果变量进行累加和统计。
2. 注释详细：通过注释解释了每个步骤的作用，使代码更加易于理解。
3. 边界情况处理：考虑了边界情况，例如，对于A2结果为0，而存在符合条件的A2数字时，不输出'N'。

代码缺点

1. 可读性：虽然逻辑清晰，但变量名（如 is_A2_no_N、A2_flag）可以更具描述性，以增加可读性。
2. 冗余判断：在最后一个循环中，对于results[i] == 0的判断有些冗余，因为A2的特殊处理可以在一个单独的步骤中完成。

时间复杂度

代码的时间复杂度主要分为两个部分：

1. 输入读取：时间复杂度为 O(N)，因为需要读取N个数字。
2. 循环处理：时间复杂度为 O(N)，因为对每个数字进行一次分类和计算。

因此，整个代码的时间复杂度为 O(N)。

空间复杂度

代码的空间复杂度主要分为以下部分：

1. 输入数据存储：需要存储N个数字，空间复杂度为 O(N)。
2. 结果变量：使用了固定数量的变量（A1, A2, A3, A4, A5，及一些辅助变量），空间复杂度为 O(1)。

因此，整个代码的空间复杂度为 O(N)。

代码改进建议

1. 变量命名：可以使用更具描述性的变量名，例如 is_A2_no_N 可以改为 a2_has_valid_numbers，A2_flag 可以改为 a2_sign。
2. 简化逻辑：可以将最后的特殊处理逻辑单独提取出来，以减少冗余判断。

---

我要更强

优化时间复杂度和空间复杂度的方法通常涉及减少不必要的计算和存储。对于这段代码，由于其已经具有线性时间复杂度（O(N)）和线性空间复杂度（O(N)），进一步的优化可能不会显著改变这些复杂度，但可以提高代码的效率和可读性。以下是一些可能的优化方法：

1. 减少重复计算：在循环中，如果某些计算是重复的，可以考虑将这些计算移出循环。
2. 使用更高效的数据结构：如果需要频繁查找或更新数据，使用合适的数据结构可以提高效率。
3. 避免不必要的类型转换：在处理数据时，尽量避免不必要的类型转换，因为这可能会增加时间开销。

由于这段代码的逻辑已经相对简单，且没有明显的重复计算或不必要的类型转换，因此直接的时间和空间优化可能有限。不过，我们可以通过改进代码结构和可读性来间接提高代码的效率。

以下是改进后的代码，虽然时间复杂度和空间复杂度没有变化，但代码结构更清晰，可读性更强：

# 读取输入，并分割成N和数字列表
N, *nums = map(int, input().split())

# 初始化结果变量
A1 = A2 = A3 = A4 = A5 = 0
a2_has_valid_numbers = False  # 标记是否存在符合A2条件的数字
a2_sign = 1  # A2的加减标志
A4_count = 0  # A4的计数器

# 遍历数字列表，计算结果
for num in nums:
    if num % 5 == 0 and num % 2 == 0:
        A1 += num
    elif num % 5 == 1:
        a2_has_valid_numbers = True
        A2 += a2_sign * num
        a2_sign *= -1
    elif num % 5 == 2:
        A3 += 1
    elif num % 5 == 3:
        A4 += num
        A4_count += 1
    elif num % 5 == 4 and num > A5:
        A5 = num

# 计算A4的平均值
if A4_count > 0:
    A4 = A4 / A4_count

# 准备输出结果
results = []
for result in [A1, A2, A3, A4, A5]:
    if result == 0 and (results.index('A2') != 1 or not a2_has_valid_numbers):
        results.append('N')
    elif results.index('A4') == 3:
        results.append(f"{result:.1f}")
    else:
        results.append(result)

# 输出结果
print(' '.join(map(str, results)))

这段代码的主要优化在于改进了代码的可读性和结构，使得逻辑更加清晰。时间复杂度和空间复杂度仍然保持为O(N)，但通过改进代码结构，可以提高代码的维护性和可理解性，这在长期运行和维护中是非常重要的。

---

哲学和编程思想

这段代码的优化涉及几个重要的哲学和编程思想，包括：

1. KISS原则（Keep It Simple, Stupid）：

   • 这个原则强调保持代码的简单性。在优化代码时，我们尽量保持逻辑的清晰和简洁，避免过度复杂的结构。例如，通过简化变量名和逻辑判断，使代码更易于理解和维护。

2. DRY原则（Don't Repeat Yourself）：

   • DRY原则鼓励开发者避免重复的代码。虽然这段代码中没有明显的重复代码，但通过优化逻辑和结构，我们减少了不必要的判断和操作，间接地遵循了DRY原则。

3. 抽象化：

   • 通过抽象化，我们可以将复杂的逻辑简化为更容易管理的部分。在这段代码中，我们将处理不同条件下的数字的逻辑抽象为几个简单的if-elif语句，使得代码更加模块化和易于理解。

4. 模块化编程：

   • 模块化编程是将程序分解为多个独立模块的思想。虽然这段代码没有明显的模块化结构，但通过将不同的计算逻辑分离到不同的变量和条件语句中，我们实际上是在进行一种简单的模块化。

5. 优化算法和数据结构：

   • 虽然这段代码的时间复杂度和空间复杂度已经是O(N)，但通过选择合适的数据结构（如使用列表来存储结果）和算法（如直接在循环中处理数据而不是在循环后处理），我们可以提高代码的效率。

6. 可读性和可维护性：

   • 在编程中，可读性和可维护性是非常重要的。通过改进变量名、简化逻辑和增加注释，我们提高了代码的可读性，使得其他开发者更容易理解和维护这段代码。

7. 测试和调试：

• 在优化代码时，我们通常会考虑如何使代码更容易测试和调试。通过保持代码的简单性和清晰性，我们可以更容易地定位和修复潜在的问题。

这些哲学和编程思想不仅适用于这段代码的优化，也是软件开发中的通用原则。通过应用这些原则，可以创建出更高效、更可靠和更易于维护的软件。

---

举一反三

根据上述提到的哲学和编程思想，以下是一些实用的技巧和建议，可以帮助你在编程中举一反三，提高代码质量和效率：

1. 保持代码简洁：

   • 使用清晰的变量名和函数名。
   • 避免不必要的复杂逻辑，尽量使用简单的控制结构。
   • 使用注释来解释复杂的逻辑或重要的决策点。

2. 避免重复代码：

   • 识别并提取重复的代码块为函数或方法。
   • 使用模板方法或策略模式来封装可变的行为。
   • 使用配置文件或环境变量来管理可变的参数，而不是硬编码。

3. 抽象化：

   • 将复杂的逻辑分解为小的、可管理的部分。
   • 使用类和对象来封装数据和操作。
   • 使用接口或抽象类来定义通用的行为，以便不同的实现可以互换。

4. 模块化编程：

   • 将代码分解为独立的模块或包，每个模块负责一个特定的功能。
   • 使用依赖注入来管理模块间的依赖关系。
   • 使用版本控制系统来管理模块的变更历史。

5. 优化算法和数据结构：

   • 了解不同数据结构和算法的优缺点，根据问题的特点选择合适的工具。
   • 使用缓存和记忆化技术来避免重复计算。
   • 使用并行和并发技术来提高性能。

6. 提高可读性和可维护性：

   • 使用一致的代码风格和格式。
   • 编写单元测试来验证代码的正确性。
   • 定期进行代码审查，以发现潜在的问题和改进点。

7. 测试和调试：

• 使用断言和日志来帮助调试。
• 编写集成测试和端到端测试来验证系统的整体行为。
• 使用版本控制系统的分支和标签来管理不同的开发和发布阶段。

通过将这些技巧应用到你的日常编程实践中，可以提高代码的质量，减少错误，并提高开发效率。记住，编程不仅仅是写代码，更是一种解决问题和创造价值的过程。

---