Ubuntu 24.04 屏蔽snap包

屏蔽

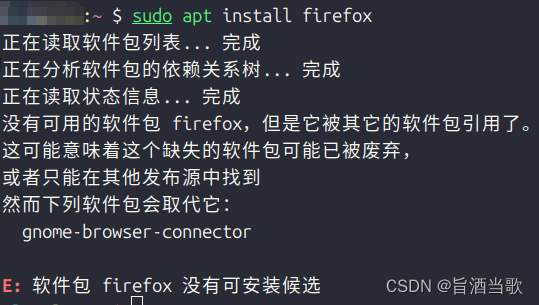
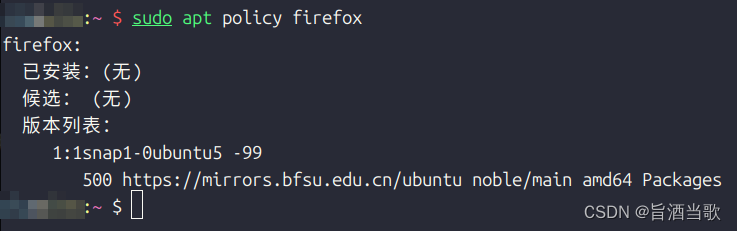
这里所说的屏蔽指的是：禁止sudo apt install firefox时安装snap版本的包。
如需卸载snap，请使用关键词搜索。

命令行

cat <<'EOF' | sudo tee /etc/apt/preferences.d/snap-apps-disable
Package: chromium* firefox* thunderbird*
Pin: version /.*snap.*/
Pin-Priority: -99
'EOF'

效果

恢复

sudo rm /etc/apt/preferences.d/snap-apps-disable

注意

1、运行代码前确保知晓代码含义，以及去除CSDN添加的尾巴。
2、本文仅做技术交流，因任何原因导致的任何问题，本文概不负责。
3、暂不清楚ubuntu源是否会增加其他 “表面上是deb其实是snap” 的软件包。