题目描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

题目分析

递归法（超出时间限制）

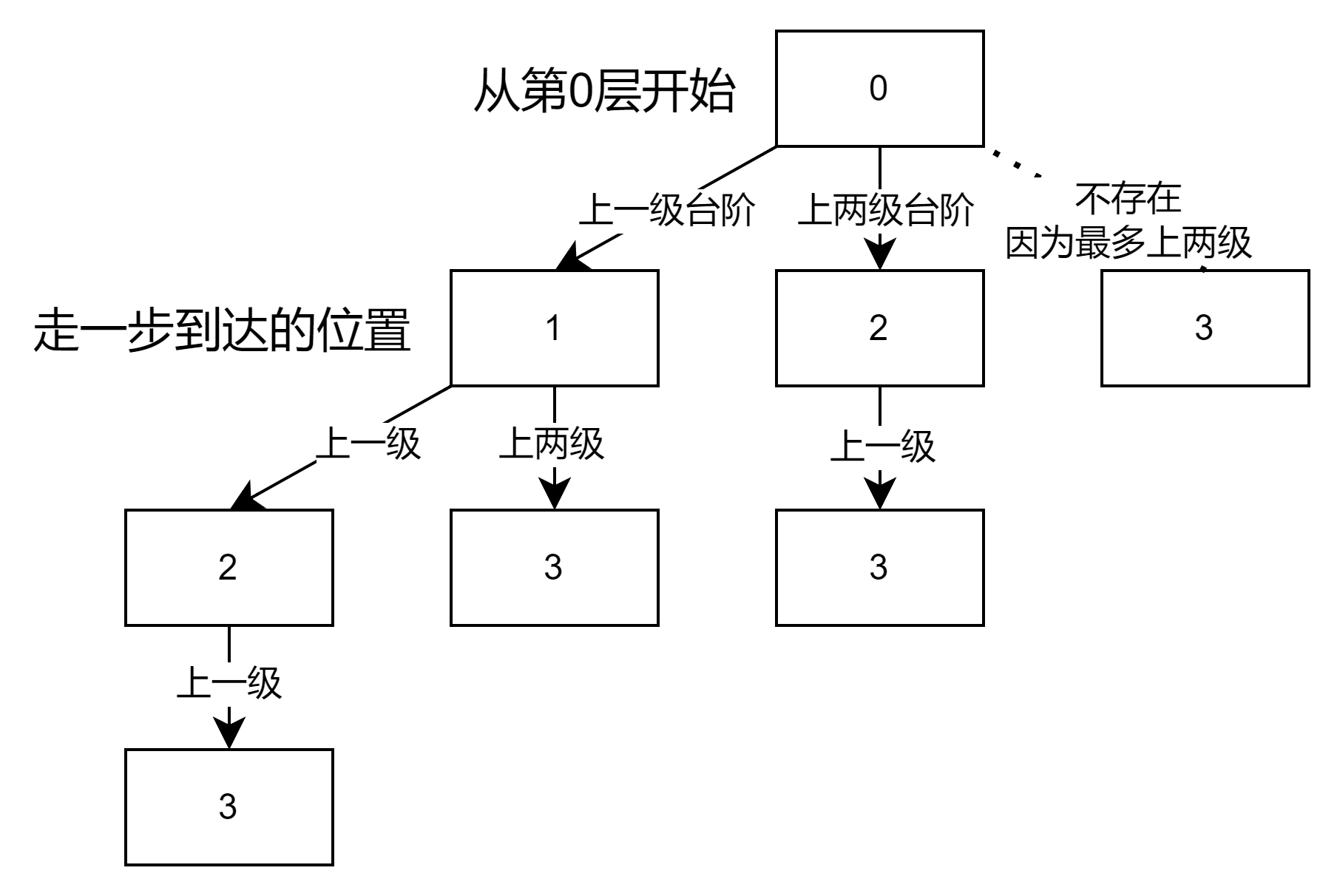
1. 递归参数与返回值
   void reversal(int i, int k)
   每次我们处理第i个台阶到第k个台阶之间的可能性。这里我把结果int cnt放在类成员中了，所以直接在函数中进行处理，不用返回。
2. 递归终止条件
   当我们处理到最上面的台阶了，也就是reversal(n, n)就可以结束当前递归。
3. 单层递归逻辑
   单层递归中，我们再将区间(i, k)细分下去：因为我们每次只能上一级或两级台阶，并且上了台阶之后才能处理更高层的范围，所以在缩小范围时，我们针对的是区间的左边。也就是：

for(int j = 1; j <= (k-i) && j <=2; j++){
            reversal(i+j, k);
        }

其中，j就是我们上台阶的可能性，它的取值要小于等于2且不能超过区间的大小。

最终的cpp递归代码：

class Solution {
private:
    int cnt;
public:
    void reversal(int i, int k){    // 在第i个台阶到第k个台阶之间做决策
        // 递归终止条件：已经到最上面的台阶，cnt加一并返回
        if(i == k){
            cnt++;
            return;
        }

        // 单层递归：从第i个台阶到第k个台阶的可能性
        // j在这里代表是上几个台阶
        for(int j = 1; j <= (k-i) && j <=2; j++){
            reversal(i+j, k);
        }
    }

    int climbStairs(int n) {
        cnt = 0;
        reversal(0, n);
        return cnt;
    }
};

动态规划

1. 确定dp数组以及下标的含义
   dp[i]：爬到第i级台阶的方法数量。

2. 确定递推公式
   dp[i] = dp[i-1] + dp[i-2]

因为我们只有两种上楼梯的方法，也即上一级台阶或两级台阶。试想：

• 我们上到第i-1级台阶时，共有d[i-1]种方法，再上一级则到达第i级台阶；
• 我们上到第i-2级台阶时，共有d[i-2]种方法，再上两级则到达第i级台阶；

上到第i级台阶也就两种情况，从第i-1级台阶再上一级，或是从第i-2级台阶再上两级，那么我们上到第i级台阶的方法不就是 dp[i-1] + dp[i-2]。这也说明了每一级台阶的状态是由前面两级台阶决定的。

3. dp数组初始化
   dp[1] = 1;
dp[2] = 2;

因为第0级台阶不存在，所以我们不必纠结dp[0]的值到底如何初始化。

4. 确定遍历顺序
   因为dp[i]是由它的前两个数决定，所以我们只能从前往后去遍历。

5. 举例推导dp数组
   例如当n=5：
   dp[1]=1;
   dp[2]=2;
   dp[3] = dp[2] + dp[1] = 3;
   dp[4] = dp[3] + dp[2] = 5;
   dp[5] = dp[4] + dp[3] = 8;

动态规划的cpp代码：

class Solution {
public:
    int climbStairs(int n) {
        if(n < 3) return n;

        // 确定dp数组以及下标含义
        vector<int> dp(n+1); //dp[i]是到达第i阶楼梯的方法总数
        
        // 初始化
        dp[1] = 1;
        dp[2] = 2;
        
        // 推导
        for(int i = 3; i <= n; i++){
            dp[i] = dp[i-1] + dp[i-2];
        }

        return dp[n];
    }
};