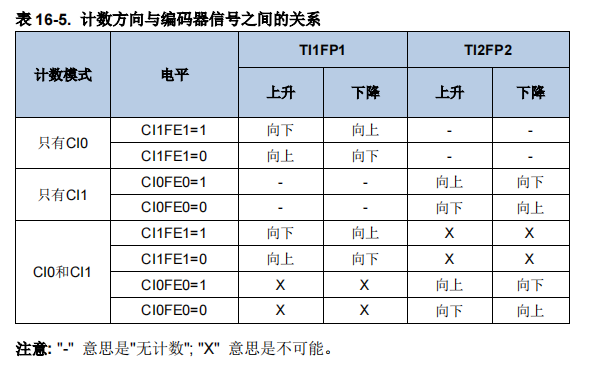
1、题目描述

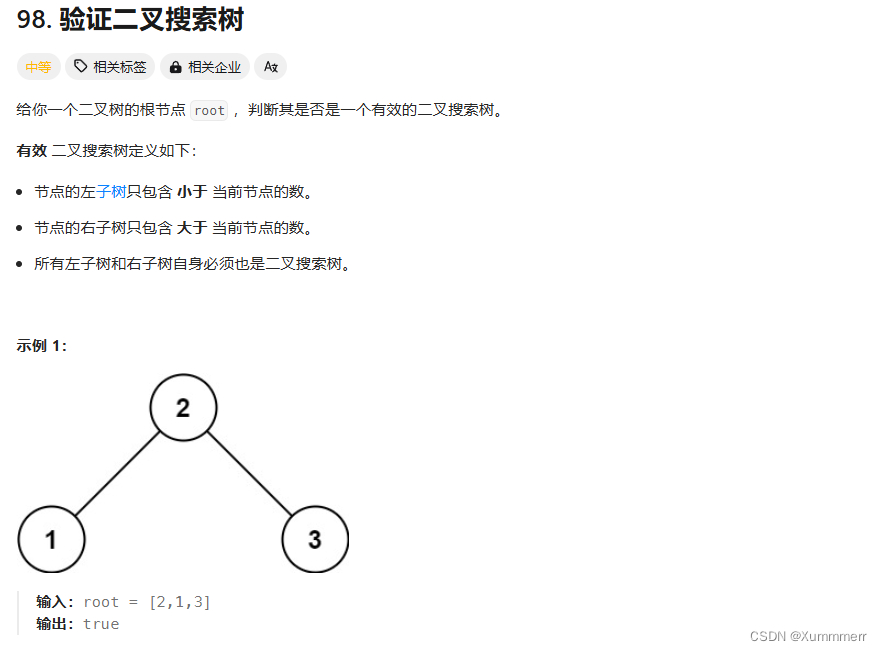
2、逻辑分析

要求给定的根节点是否是有效的二叉树。有效的二叉搜索树定义如上。那么如何求解呢？题解给出了两张求解方法：递归、中序遍历。这边倾向于中序遍历，中序遍历后的二叉树是升序排序的，以这个性质即可解题。

3、代码演示

public boolean isValidBST(TreeNode root) {
        // 使用一个栈来辅助进行中序遍历
        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        // 初始化一个比任何可能的节点值都要小的值，用来比较后续的中序遍历值
        double temp = -Double.MAX_VALUE;
        // 当栈不为空或者当前节点不为空时，循环继续
        while(!stack.isEmpty() || root != null){
            // 将当前节点以及它的所有左子节点压入栈中
            while(root != null){
                stack.push(root);
                root = root.left;
            }
             // 从栈中弹出一个节点，并检查其值是否满足BST的特性
            root = stack.pop();
            // 如果当前节点的值小于等于前一个中序遍历节点的值（temp），则不是BST  
            // 注意：这里使用了小于等于，因为BST中不允许有重复值 
            if(root.val <= temp){
                return false;
            }
            // 更新中序遍历的节点值
            temp = root.val;
            // 继续遍历右子树
            root = root.right;
        }
        // 如果遍历完整个树后都没有返回false，则说明这是一个有效的BST
        return true;
    }

这个算法使用了中序遍历的思想，但并不是真正地进行中序遍历并存储所有值。它只维护了一个变量 temp 来保存上一个遍历到的节点的值，并与当前节点的值进行比较。如果满足BST的特性，则继续遍历；否则，直接返回 false。

4、复杂度分析

• 时间复杂度：O(n)。n为节点数，需要访问n个节点。
• 空间复杂度：O(n)。需要一个栈来存节点。

ok，又水了一题哈哈哈哈，crying！！！