减治法介绍
减治法思想
分治法是将一个大问题划分为若干个子问题,分别求各个子问题,然后把子问题的解进行合并得到原问题的解。
减治法同样是把一个大问题划分为若干个子问题,但是并不是求解所有的子问题,因为原问题的解就在其中一个子问题当中,所以只求解其中一个子问题。
与分治法不同的就在于这个“减”字上,会不断的将原问题的规模减小,直到找到最终的解。
减治法求解过程:
减治法将原问题分解为若干个子问题,并且原问题(规模为n)的解和子问题(规模为 n/2 或 n-1)的解之间存在某种确定的关系:
原问题的解只存在其中一个子问题中。
原问题的解与其中一个子问题的解之间存在某种对应关系。
那么求解过程就可以确定了:
- 将原问题分解为规模较小的子问题
- 找到原问题的解所在的子问题
- 重复第1、2步直到得到子问题的解
- 根据子问题的解,直接得出或计算出原问题的解。
前面蛮力法中使用的案例选择排序其实也是一种减治法,因为其每次都会去除掉一个元素,使问题的规模减一。
减治法案例-二分查找
分析:
二分查找每次计算完数组中间值,与待查找元素对比之后,会使下一次待查找的区间减半,所以二分查找属于比较经典的减治。
过程如下:
- 取有序序列的中间值与待查找值比较。
- 若中间值与待查找值相同则查找成功。
- 若中间值比待查找值小,则在中间记录的左边区间查找。
- 若中间值比待查找值大,则在中间记录的右边区间查找。
- 重复上述1~4过程,直到查找成功或区间无记录。
过程图解:
1、初始化
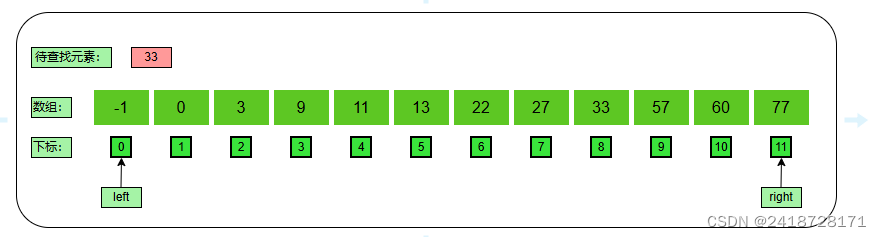
有序数组:{ -1、0、3、9、11、13、22、27、55、57、60、77 }
待查找元素: 33
初始化:左下标为0(left = 0)、右下标为11(right=11)
2、第一趟比较
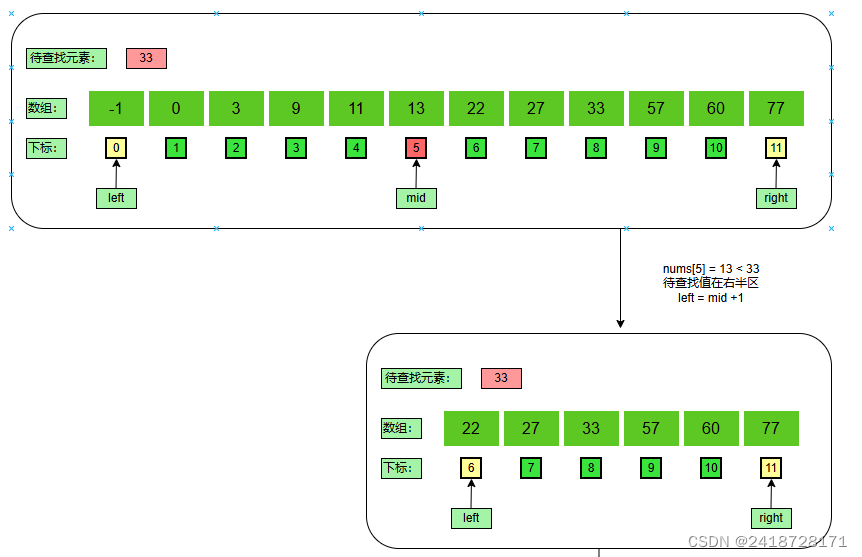
计算中间值:
m i d = l e f t + ( r i g h t − l e f t ) / 2 = 0 + ( 11 − 0 ) / 2 = 5 mid = left + (right - left) / 2 = 0 + (11 - 0) / 2 = 5 mid=left+(right−left)/2=0+(11−0)/2=5
减少规模:
n u m s [ 5 ] = 13 < 33 nums[5] = 13 < 33 nums[5]=13<33,带查找值在数组右半区,则 l e f t = m i d + 1 = 5 + 1 = 6 left = mid + 1 = 5 + 1 = 6 left=mid+1=5+1=6。
3、第二躺比较
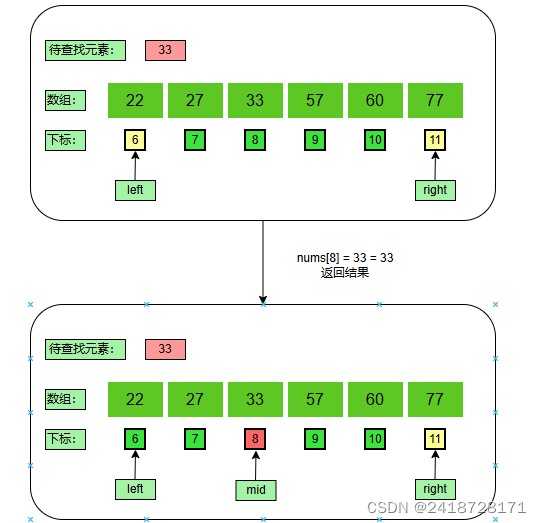
计算中间值:
m i d = l e f t + ( r i g h t − l e f t ) / 2 = 6 + ( 11 − 6 ) / 2 = 8 mid = left + (right - left) / 2 = 6 + (11 - 6) / 2 = 8 mid=left+(right−left)/2=6+(11−6)/2=8
得到结果:
n u m s [ 8 ] = 33 = 33 nums[8] = 33 = 33 nums[8]=33=33,找到带查找值在数组中的下标8,查找结束。
代码实现:
public static int execute(int[] data, int key) {
int leftIndex = 0, rightIndex = data.length - 1;
int midIndex = -1;
// 当左下标不再小于右下标,说明区间内已经没有元素,即数组内没有待查找元素
while (leftIndex < rightIndex) {
midIndex = (rightIndex - leftIndex) / 2 + leftIndex;
// 找到就直接返回
if (data[midIndex] == key) {
return midIndex;
//中间值小于待查找值,待查找值在数组右半区域
} else if (data[midIndex] < key) {
leftIndex = midIndex + 1;
//中间值大于待查找值,待查找值在数组左半区域
} else {
rightIndex = midIndex - 1;
}
}
return data[midIndex] == key ? midIndex : -1;
}