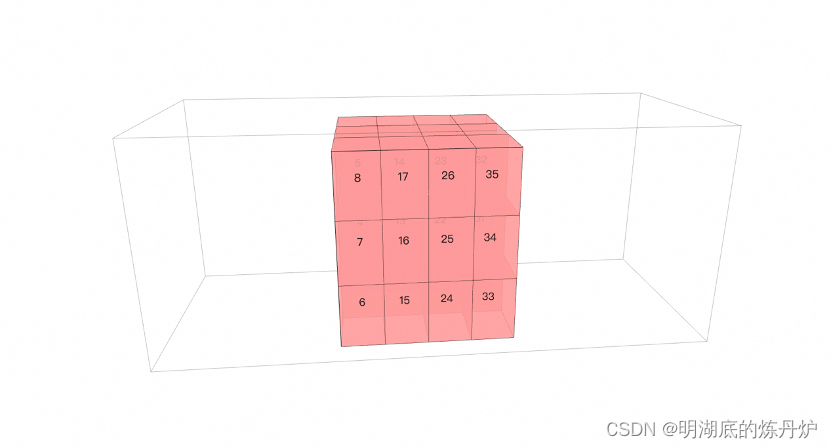
搜索二叉树的概念及实现

news2024/11/16 11:41:20

搜索二叉树的概念

搜索二叉树规则（左小右大）： 

  1. 非空左子树的键值小于其根节点的键值
  2. 非空右子树的键值大于其根节点的键值
  3. 左右子树均为搜索二叉树

 如图：

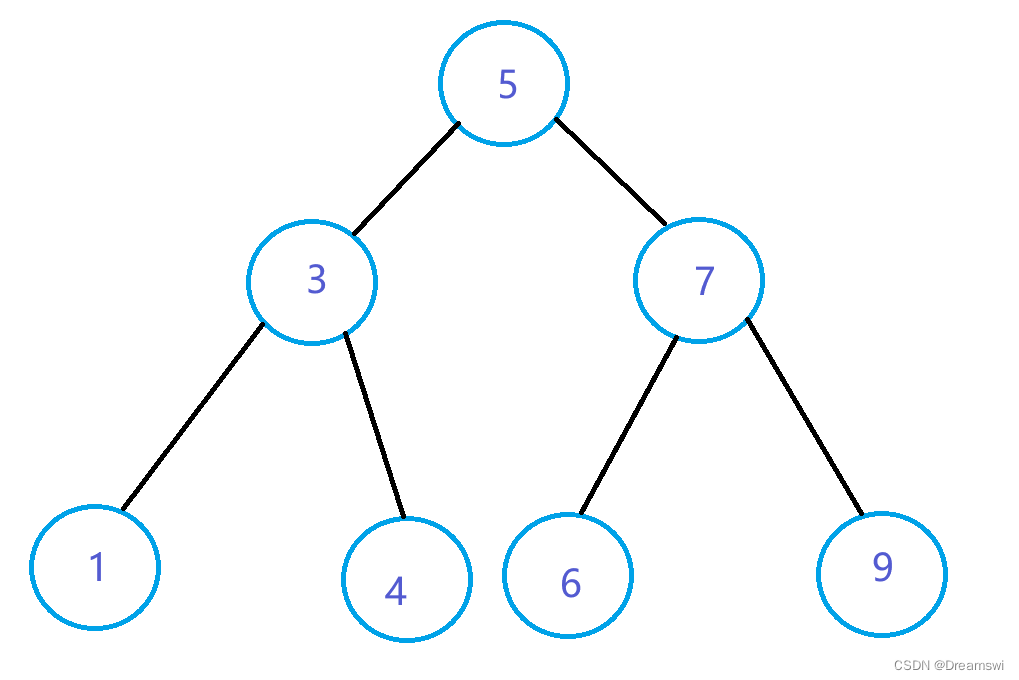
 在搜索时，若大于根，则去右子树寻找；若小于根，则去左子树寻找。直到找到或为空结束。在理想状态下只需查找树的高度次。

代码实现

#pragma once
#include<iostream>
using namespace std;

//key版本
namespace key
{
	template<class T>
	struct BSTreeNode
	{
		BSTreeNode<T>* _left;
		BSTreeNode<T>* _right;
		T _key;

		BSTreeNode(const T& key)
			:_left(nullptr)
			,_right(nullptr)
			,_key(key)
		{}
	};

	template<class T>
	class BSTree
	{
		typedef BSTreeNode<T> Node;
	public:
		bool Insert(const T& key)
		{
			if (root == nullptr)
			{
				root = new Node(key);
				return true;
			}

			Node* parent = nullptr;
			Node* cur = root;
			while (cur)
			{
				if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else
				{
					return false;
				}
			}
			cur = new Node(key);
			if (parent->_key > key)
			{
				parent->_left = cur;
			}
			else
			{
				parent->_right = cur;
			}

			return true;
		}

		Node* find(const T& key)
		{
			Node* cur = root;
			while (cur)
			{
				if (cur->_key > key)
				{
					cur = cur->_left;
				}
				else if (cur->_key < key)
				{
					cur = cur->_right;
				}
				else
				{
					return cur;
				}
			}

			return nullptr;
		}

		bool Erase(const T& key)
		{
			Node* parent = nullptr;
			Node* cur = root;
			while (cur)
			{
				if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else
				{
					if (cur->_left == nullptr)
					{
						if (cur == root)
						{
							root = cur->_right;
						}
						else
						{
							if (cur == parent->_left)
							{
								parent->_left = cur->_right;
							}
							else
							{
								parent->_right = cur->_right;
							}
						}
						delete cur;
					}
					else if (cur->_right == nullptr)
					{
						if (cur == root)
						{
							root = cur->_left;
						}
						else
						{
							if (cur == parent->_left)
							{
								parent->_left = cur->_left;
							}
							else
							{
								parent->_right = cur->_left;
							}
						}
						delete cur;
					}
					else
					{
						Node* rightMinParent = cur;
						Node* rightMin = cur -> _right;
						while (rightMin->_left)
						{
							rightMinParent = rightMin;
							rightMin = rightMin->_left;
						}
						swap(cur->_key, rightMin->_key);
						
						//假设没有进循环，那么rightMin = cur->_right，所以要判断一下。
						if (rightMin == rightMinParent->_left)
							rightMinParent->_left = rightMin->_right;
						else
							rightMinParent->_right = rightMin->_right;
						delete rightMin;
					}
					return true;
				}
			}

			return false;
		}

		void InOrder()
		{
			_InOrder(root);
			cout << endl;
		}
	private:
		void _InOrder(Node* root)
		{
			if (root == nullptr)
			{
				return;
			}

			_InOrder(root->_left);
			cout << root->_key << " ";
			_InOrder(root->_right);
		}

		Node* root = nullptr;
	};
}


//key_value版本
namespace key_value
{
	template<class T, class V>
	struct BSTreeNode
	{
		BSTreeNode<T,V>* _left;
		BSTreeNode<T,V>* _right;
		T _key;
		V _value;

		BSTreeNode(const T& key,const V& value = V())
			:_left(nullptr)
			, _right(nullptr)
			, _key(key)
			,_value(value)
		{}
	};

	template<class T, class V>
	class BSTree
	{
		typedef BSTreeNode<T,V> Node;
	public:
		bool Insert(const T& key, const V& value)
		{
			if (root == nullptr)
			{
				root = new Node(key,value);
				return true;
			}

			Node* parent = nullptr;
			Node* cur = root;
			while (cur)
			{
				if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else
				{
					return false;
				}
			}
			cur = new Node(key, value);;
			if (parent->_key > key)
			{
				parent->_left = cur;
			}
			else
			{
				parent->_right = cur;
			}

			return true;
		}

		Node* find(const T& key)
		{
			Node* cur = root;
			while (cur)
			{
				if (cur->_key > key)
				{
					cur = cur->_left;
				}
				else if (cur->_key < key)
				{
					cur = cur->_right;
				}
				else
				{
					return cur;
				}
			}

			return nullptr;
		}

		bool Erase(const T& key)
		{
			Node* parent = nullptr;
			Node* cur = root;
			while (cur)
			{
				if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else
				{
					if (cur->_left == nullptr)
					{
						if (cur == root)
						{
							root = cur->_right;
						}
						else
						{
							if (cur == parent->_left)
							{
								parent->_left = cur->_right;
							}
							else
							{
								parent->_right = cur->_right;
							}
						}
						delete cur;
					}
					else if (cur->_right == nullptr)
					{
						if (cur == root)
						{
							root = cur->_left;
						}
						else
						{
							if (cur == parent->_left)
							{
								parent->_left = cur->_left;
							}
							else
							{
								parent->_right = cur->_left;
							}
						}
						delete cur;
					}
					else
					{
						Node* rightMinParent = cur;
						Node* rightMin = cur->_right;
						//找cur右子树最小的值
						while (rightMin->_left)
						{
							rightMinParent = rightMin;
							rightMin = rightMin->_left;
						}
						swap(cur->_key, rightMin->_key);
						swap(cur->_value, rightMin->_value);

						//假设没有进循环，那么rightMin = cur->_right，所以要判断一下。
						if (rightMin == rightMinParent->_left)
							rightMinParent->_left = rightMin->_right;
						else
							rightMinParent->_right = rightMin->_right;
						delete rightMin;
					}
					return true;
				}
			}

			return false;
		}

		void InOrder()
		{
			_InOrder(root);
			cout << endl;
		}
	private:
		void _InOrder(Node* root)
		{
			if (root == nullptr)
			{
				return;
			}

			_InOrder(root->_left);
			cout << root->_key << " " << root->_value << endl;
			_InOrder(root->_right);
		}

		Node* root = nullptr;
	};

}

Insert函数详解

bool Insert(const T& key)
		{
            //假设根节点为空
			if (root == nullptr)
			{
				root = new Node(key);
				return true;
			}
            

            //根节点不为空
			Node* parent = nullptr;
			Node* cur = root;
			while (cur)
			{
				if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else//等于
				{
                    //出现重复，不插入
					return false;
				}
			}

            //将新节点连接入树
			cur = new Node(key);
			if (parent->_key > key)
			{
				parent->_left = cur;
			}
			else
			{
				parent->_right = cur;
			}

			return true;
		}

（1）若根节点为空，为其新建（new）一个节点。

（2）若根节点不为空，则根据二叉树定义（大于当前根的键值进右子树，小于当前根的键值进左子树）去寻找合适的位置新建节点。出现等于即重复的情况不插入。

（3）新节点连接入树时，要检查他是parent的左节点还是右节点，判断完毕后再连接。

 Erase函数详解

bool Erase(const T& key)
		{
			Node* parent = nullptr;
			Node* cur = root;
			while (cur)
			{
				if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else//找到删除目标
				{
                    //假设目标左子树为空
					if (cur->_left == nullptr)
					{
						if (cur == root)
						{
							root = cur->_right;
						}
						else
						{
							if (cur == parent->_left)
							{
								parent->_left = cur->_right;
							}
							else
							{
								parent->_right = cur->_right;
							}
						}
						delete cur;
					}
                         //假设目标右子树为空
					else if (cur->_right == nullptr)
					{
						if (cur == root)
						{
							root = cur->_left;
						}
						else
						{
							if (cur == parent->_left)
							{
								parent->_left = cur->_left;
							}
							else
							{
								parent->_right = cur->_left;
							}
						}
						delete cur;
					}
					else//左右子树都不为空
					{
						Node* rightMinParent = cur;
						Node* rightMin = cur -> _right;
						while (rightMin->_left)
						{
							rightMinParent = rightMin;
							rightMin = rightMin->_left;
						}
						swap(cur->_key, rightMin->_key);
						
						//假设没有进循环，那么rightMin = cur->_right，所以要判断一下。
						if (rightMin == rightMinParent->_left)
							rightMinParent->_left = rightMin->_right;
						else
							rightMinParent->_right = rightMin->_right;
						delete rightMin;
					}
					return true;
				}
			}

			return false;
		}

（1）第一步寻找删除目标（有可能是根节点），找不到返回false，表示删除失败。

（2）删除

  1. 目标左子树为空
  2. 目标右子树为空
  3. 目标左右子树都不为空

左子树为空

删除目标不是根节点时，让目标的父节点指向他的右子树。当然也要判断目标是他的父节点的左子树还是右子树。

为父节点的左子树：

 

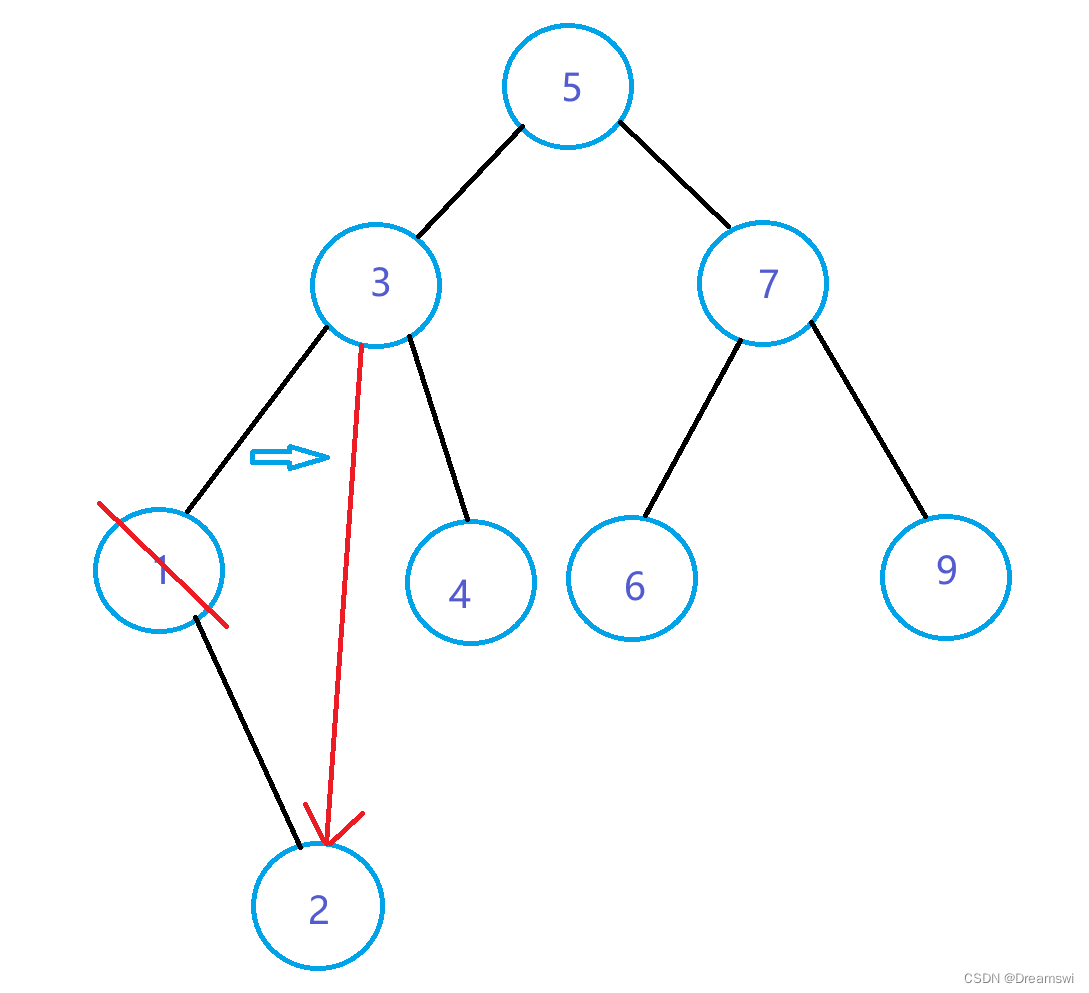
 为父节点的右子树：

 目标为根节点：

 

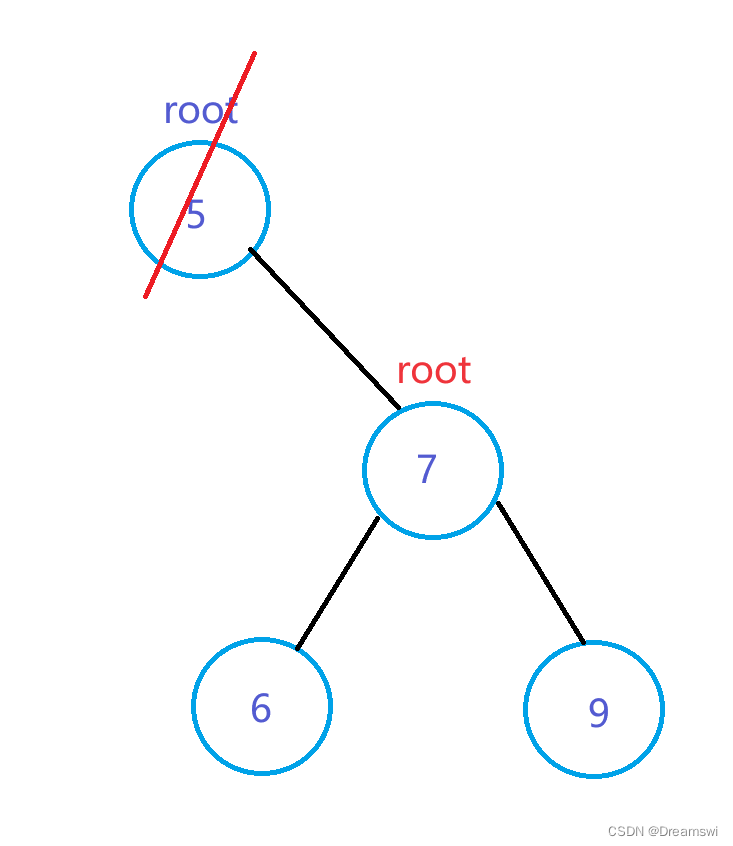
 （右子树为空的情况只是与左子树为空方向相反，不过多赘述）

左右子树都不为空时

交换    目标的键值   和   目标的右子树中的最左节点的键值    ，然后让最左节点的父节点指向最左节点的右子树（因为是最左节点，所以左子树一定为空，右子树可能为空可能不为空），最后将这个最左节点删除。

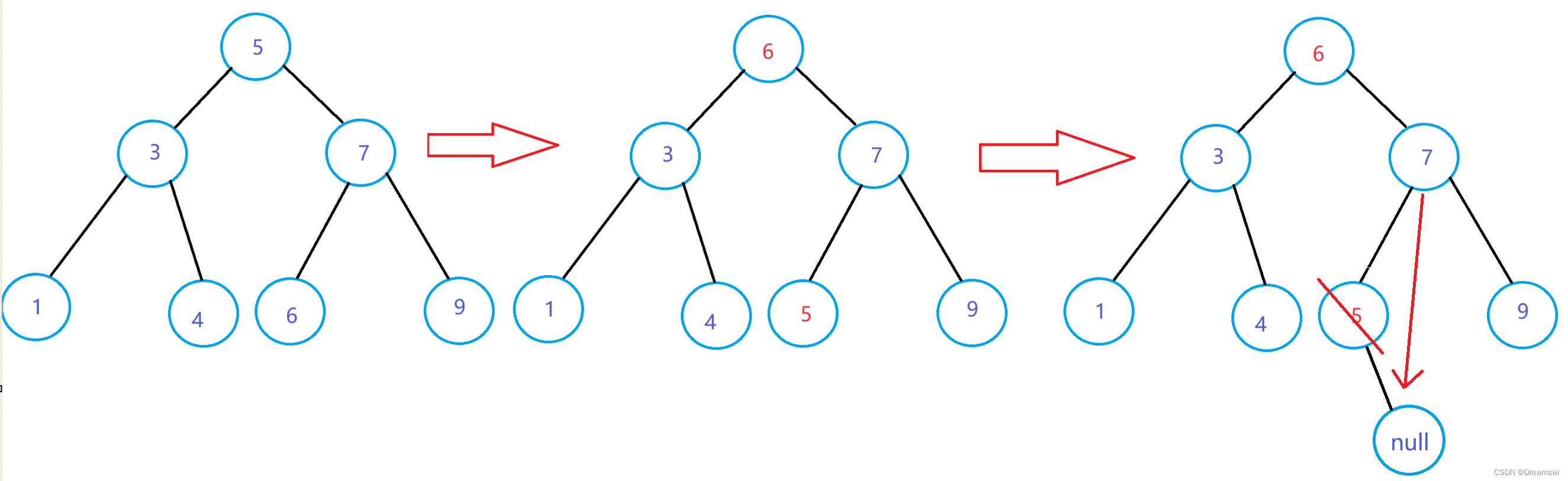
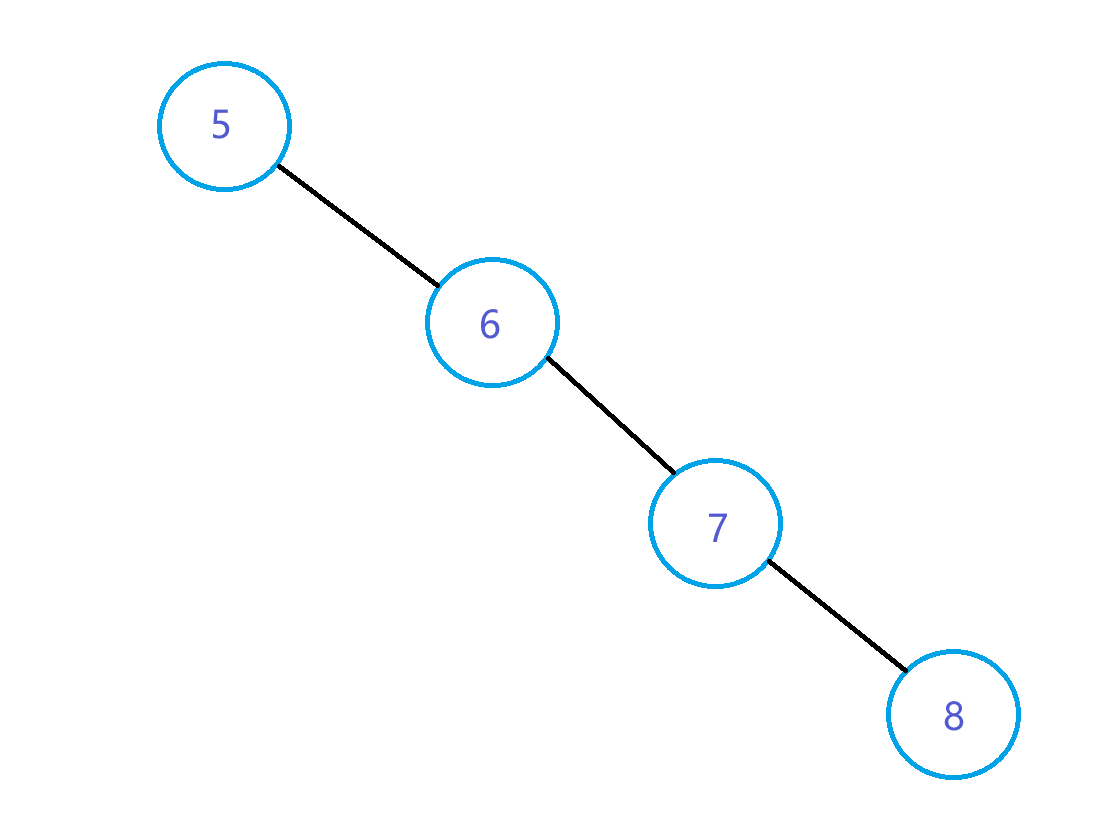
 让最左节点的父节点指向最左节点的右子树前，也要判断该最左节点是否是其父节点的左子树，因为有可能出现图中的情况。

此时右子树最左节点是7，但他却是父节点的右子树。此时是父节点的右指向最左节点的右子树，而不是父节点的左去指向。

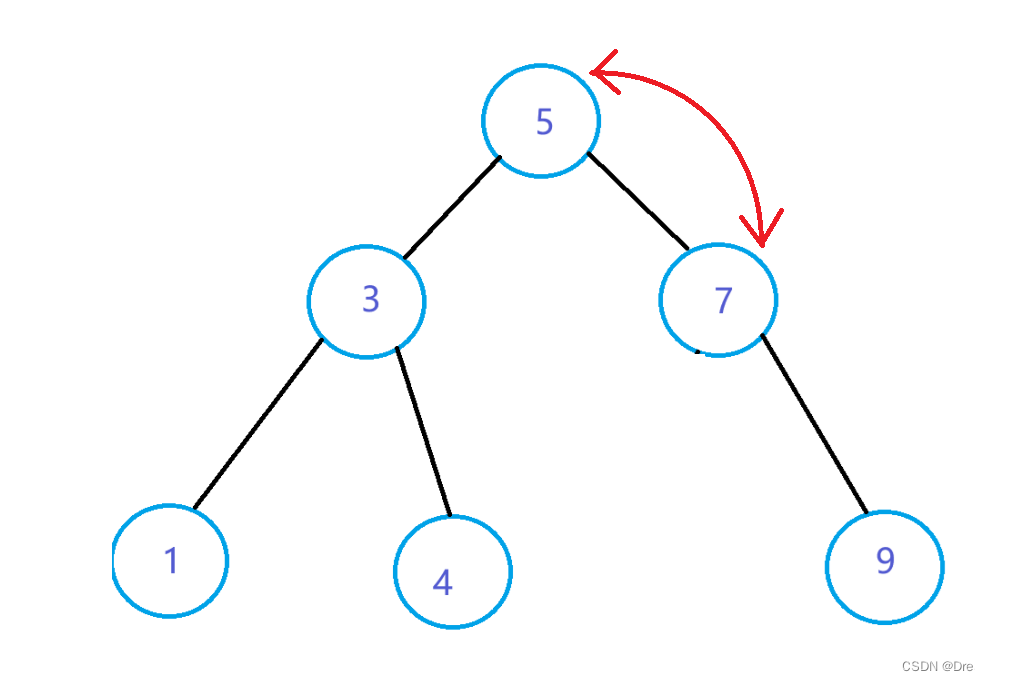
原理

删除后要保持树还是搜索二叉树。那么首先先理清一下节点键值的关系。

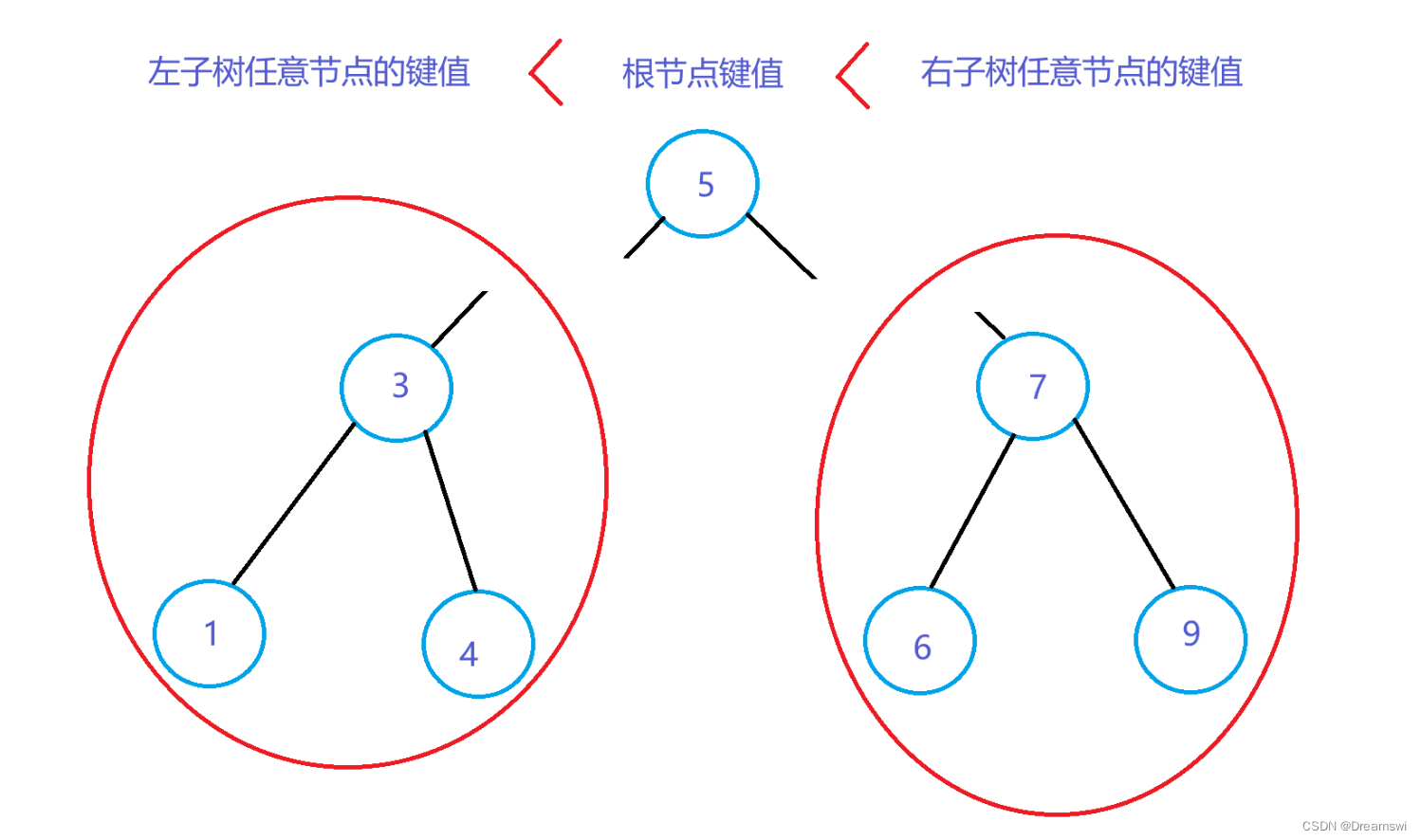
 所以我们是希望保持如图的节点关系，那么右子树的最左节点满足做根节点条件。

因为在任意树中都有    右大于根大于左    ，所以该树最左节点存储最小键值。

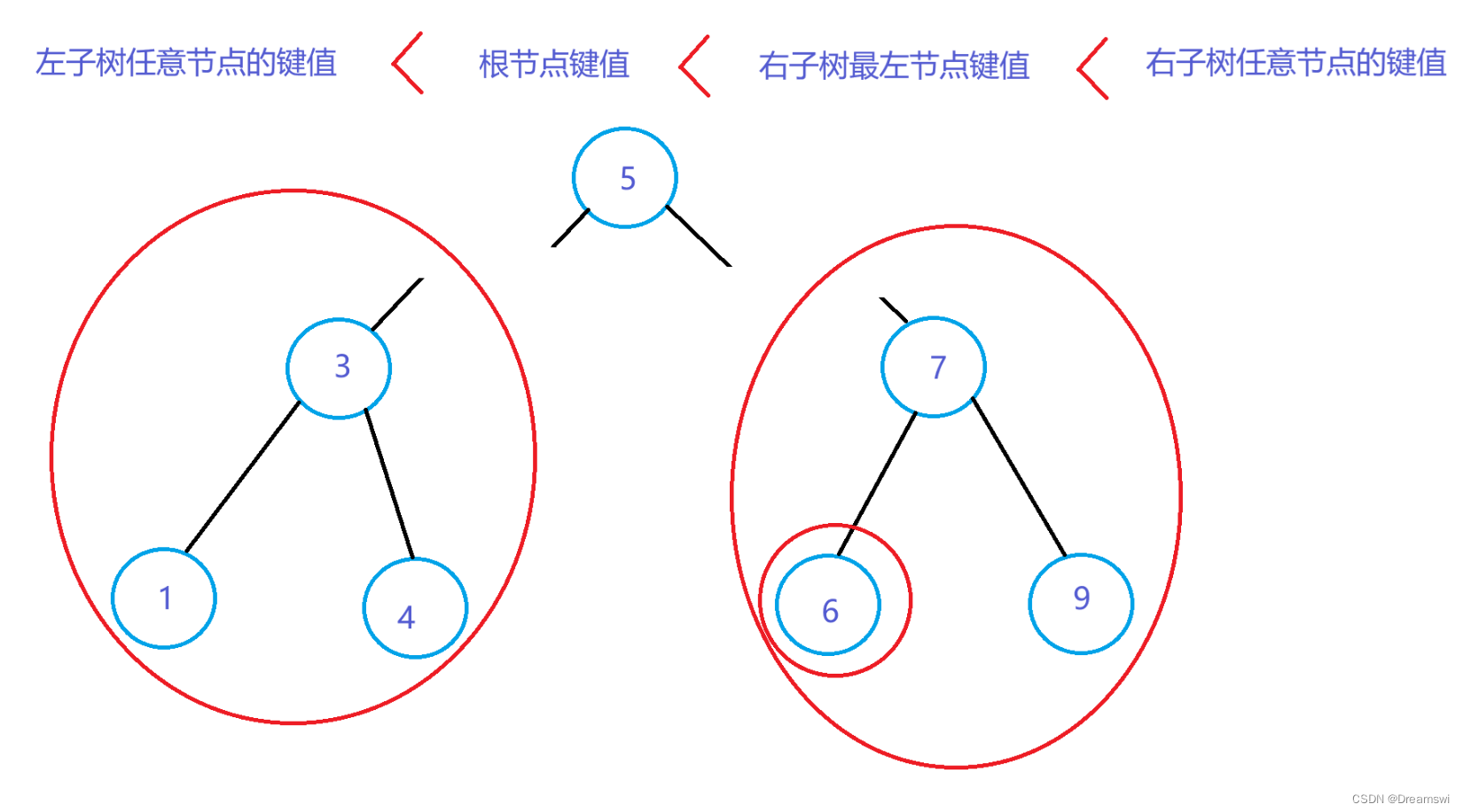
特殊存储情况 

当出现顺序插入时，会呈现出这样的情况，这个时候遍历的时间复杂度就退化到了O(n)，此时搜索二叉树就失去了意义。不过平衡二叉树和红黑树解决了高度不平衡导致搜索效率下降的问题。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1818308.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

基于单片机的多功能智能小车设计

基于单片机的多功能智能小车设计

第一章 绪论 1.1 课题背景和意义 随着计算机、微电子、信息技术的快速发展，智能化技术的发展速度越来越快，智能化与人们生活的联系也越来越紧密，智能化是未来社会发展的必然趋势。智能小车实际上就是一个可以自由移动的智能机器人，比较适合在人们无法工作的地方工作，也可…
阅读更多...
基于WPF技术的换热站智能监控系统06--实现左侧故障统计

基于WPF技术的换热站智能监控系统06--实现左侧故障统计

1、区域划分 2、ui实现 这里使用的是livechart的柱状图呈现的 3、运行效果 走过路过不要错过&#xff0c;点赞关注收藏又圈粉&#xff0c;共同致富&#xff0c;为财务自由作出贡献
阅读更多...
【git使用二】gitee远程仓库创建与本地git命令用法

【git使用二】gitee远程仓库创建与本地git命令用法

目录 gitee介绍 管理者注册gitee账号 管理者在gitee网站上创建远程仓库 每个开发者安装git与基本配置 1.git的下载和安装 2.配置SSH公钥 3.开发者信息配置 git命令用法 gitee介绍 Gitee&#xff08;又称码云&#xff09;是一个基于Git的代码托管服务&#xff0c;由开源…
阅读更多...
python数据分析-量化分析

python数据分析-量化分析

一、研究背景 随着经济的发展和金融市场的不断完善&#xff0c;股票投资成为了人们重要的投资方式之一。汽车行业作为国民经济的重要支柱产业&#xff0c;其上市公司的股票表现备受关注。Fama-French 三因子模型是一种广泛应用于股票市场的资产定价模型&#xff0c;它考虑了市场…
阅读更多...
vue3中用setup写的数据，不能动态渲染（非响应式）解决办法

vue3中用setup写的数据，不能动态渲染（非响应式）解决办法

相比于2.0&#xff0c;vue3.0在新增了一个setup函数&#xff0c;我们在setup中可以写数据也可以写方法&#xff0c;就像我们以前最开始学习js一样&#xff0c;在js文件中写代码。 For instance <template><div class"person"><h2>姓名&#xff1…
阅读更多...
中电联系列四：rocket手把手教你理解中电联协议！

中电联系列四：rocket手把手教你理解中电联协议！

分享《慧哥的充电桩开源SAAS系统&#xff0c;支持汽车充电桩、二轮自行车充电桩。》 电动汽车充换电服务信息交换 第4部分&#xff1a;数据传输与安全 Interactive of charging and battery swap service information for electric vehicle Part 4:Data transmission and secu…
阅读更多...
平安科技智能运维案例

平安科技智能运维案例

平安科技智能运维案例 在信息技术迅速发展的背景下&#xff0c;平安科技面临着运维规模庞大、内容复杂和交付要求高等挑战。通过探索智能运维&#xff0c;平安科技建立了集中配置管理、完善的运营管理体系和全生命周期运维平台&#xff0c;实施了全链路监控&#xff0c;显著提…
阅读更多...
基于块生成最大剩余空间的三维装箱算法

基于块生成最大剩余空间的三维装箱算法

问题简介 三维装箱问题&#xff08;3D Bin Packing Problem&#xff0c;3D BPP&#xff09;是一类组合优化问题。它涉及到将一定数量的三维物品放入一个或多个三维容器&#xff08;称为“箱子”&#xff09;中&#xff0c;同时遵循一定的约束&#xff0c;通常目标是最大化空间…
阅读更多...
2024/06/13--代码随想录算法2/17| 62.不同路径、63. 不同路径 II、343. 整数拆分 （可跳过）、96.不同的二叉搜索树 （可跳过）

2024/06/13--代码随想录算法2/17| 62.不同路径、63. 不同路径 II、343. 整数拆分 （可跳过）、96.不同的二叉搜索树 （可跳过）

62.不同路径 力扣链接 动态规划5步曲 确定dp数组&#xff08;dp table&#xff09;以及下标的含义&#xff1a; dp[i][j] &#xff1a;表示从&#xff08;0 &#xff0c;0&#xff09;出发&#xff0c;到(i, j) 有dp[i][j]条不同的路径。确定递推公式&#xff0c;dp[i][j] d…
阅读更多...
听说前端都是切图仔，所以学了PS

听说前端都是切图仔，所以学了PS

PS 从零开始-基础篇 什么话都不想说了&#xff0c;前端以死后端已死&#xff0c;毁灭即是新生&#xff0c;我要开始追梦了&#xff0c; 从小就希望&#xff0c;制作一款自己的游戏&#x1f3ae;去学了编程&#xff0c;了解了&#xff1a;Java、C#、前端... 不小心入了web领域…
阅读更多...
分享一个开发者工具

分享一个开发者工具

网站地址&#xff1a;https://daxia.olalo.asia/计算器 IP地址查询 BMI体脂计算 AI ChatGPT GPT 黄历 图片缩放 图片裁剪 图片水印 图片拼接 json查看器 二维码识别 二维码生成 Base64编解码 时间戳 天气 取色器 拾色器https://daxia.olalo.asia/ 很干净的一个小网站&#xff0…
阅读更多...
ppt添加圆角矩形，并调整圆角弧度方法

ppt添加圆角矩形，并调整圆角弧度方法

一、背景 我们看的论文&#xff0c;许多好看的图都是用PPT做的&#xff0c;下面介绍用ppt添加圆角矩形&#xff0c;并调整圆角弧度方法。 二、ppt添加圆角矩形&#xff0c;并调整圆角弧度 添加矩形&#xff1a; 在顶部工具栏中&#xff0c;点击“插入”选项卡。 在“插图”…
阅读更多...
Llama-3安装方法及应用

Llama-3安装方法及应用

Hi~&#xff01;这里是奋斗的小羊&#xff0c;很荣幸您能阅读我的文章&#xff0c;诚请评论指点&#xff0c;欢迎欢迎 ~~ &#x1f4a5;&#x1f4a5;个人主页&#xff1a;奋斗的小羊 &#x1f4a5;&#x1f4a5;所属专栏&#xff1a;C语言 &#x1f680;本系列文章为个人学习…
阅读更多...
【日记】第一次养植物，没什么经验……（781 字）

【日记】第一次养植物，没什么经验……（781 字）

正文 前两天梦见灵送的几盆植物全都死掉了。梦里好伤心。醒来与她说这件事&#xff0c;她宽慰我说&#xff0c;梦都是反着的&#xff0c;肯定能活得很好的。于是忽然记起昨天给植物换水时&#xff0c;文竹的根居然从花盆底部伸吊了出来&#xff0c;以前都没有这种情况来着&…
阅读更多...
为什么要用AI大模型？

为什么要用AI大模型？

前言 2021 年 8 月份&#xff0c;李飞飞和 100 多位学者联名发表一份 200 多页的研究报告《On the Opportunities and Risk of Foundation Models》&#xff0c;深度地综述了当前大规模预训练模型面临的机遇和挑战。 语言模型已经深刻变革了自然语言处理领域的研究和实践。近…
阅读更多...
ui自动化中，几种文件上传整理2024

ui自动化中，几种文件上传整理2024

input标签的 对于input标签实现的文件上传&#xff0c;看成输入框&#xff0c;直接send_keys 非input标签的 要使用第三方库&#xff1a; 方式1&#xff1a; pip install pypiwin32 要点&#xff1a;图片路径要写路径 方式2&#xff1a;pip install pyautogui 方式3&#…
阅读更多...
Idea | Idea提交.properties文件乱码问题

Idea | Idea提交.properties文件乱码问题

这里 Transparent natice-to-ascii conversion 自动转换ASCII码 千万别勾选
阅读更多...
ssm情侣购物系统-计算机毕业设计源码02387

ssm情侣购物系统-计算机毕业设计源码02387

目 录 摘要 1 绪论 1.1 开发背景与意义 1.2开发意义 1.3Vue.js 主要功能 1.3论文结构与章节安排 2 情侣购物系统系统分析 2.1 可行性分析 2.2 系统流程分析 2.2.1 数据流程 3.3.2 业务流程 2.3 系统功能分析 2.3.1 功能性分析 2.3.2 非功能性分析 2.4 系统用例分…
阅读更多...
《吸血鬼猎人D》观后感

《吸血鬼猎人D》观后感

前言 在B站无意中发现了一部动漫电影《吸血鬼猎人D》&#xff0c;看着封面还不错&#xff0c;就试着点开了视频&#xff0c;看了一会儿&#xff0c;发现画面很精美&#xff0c;人物造型高大威猛&#xff0c;肌肉线条清晰可见。如果我没记错的话&#xff0c;这种风格在日本动漫中…
阅读更多...
当我用AI写高考作文题目，你给打几分？

当我用AI写高考作文题目，你给打几分？

2024高考作文题目&#xff1a; 随着互联网的普及、人工智能的应用&#xff0c;越来越多的问题能很快得到答案。那么&#xff0c;我们的问题是否会越来越少&#xff1f;以上材料引发了你怎样的联想和思考&#xff1f;请写一篇文章。要求&#xff1a;选准角度&#xff0c;确定立…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023