问题简介

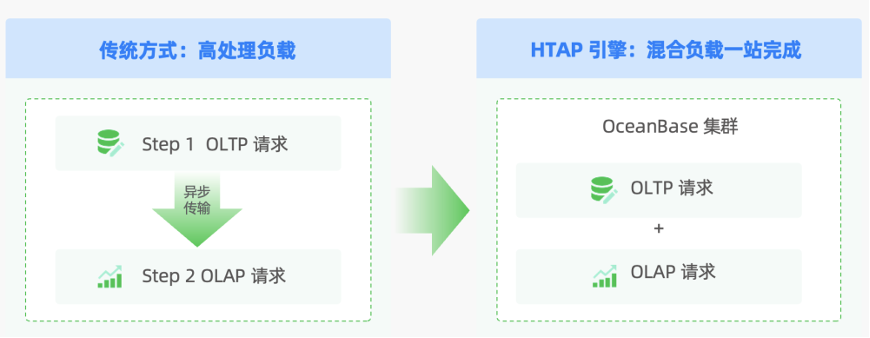
三维装箱问题（3D Bin Packing Problem，3D BPP）是一类组合优化问题。它涉及到将一定数量的三维物品放入一个或多个三维容器（称为“箱子”）中，同时遵循一定的约束，通常目标是最大化空间的利用率，这意味着希望尽可能的填满容器，减少浪费空间。三维装箱问题有很多变体，但大多数都包含以下几个基本特点和约束条件：

（1）尺寸限制：每个物品和箱子都有明确的长、宽、高三个维度。

（2）不重叠：箱内的物品间不能重叠，即每个物品都需要在箱子内有明确的位置，并且物品之间不能相互穿透。

（3）方向性：在一些情况下，物品的放置可能有方向性的限制，例如，某些物品不能旋转到任意方向，或者因为稳定性、使用性等问题有特定的放置方向。

（4）容量及重量限制：物品的总体积/总重量不能超过箱子的容积/承重。

（5）装载范围约束：物品在箱子中占据的空间有一定范围约束，例如在长度方向不能超过一定值。

三维装箱问题在现实生活中有许多应用，比如集装箱装货、仓库货物存储、行李装车等。又由于问题属于NP-hard问题，这意味着找到最优解的计算复杂度随着问题规模的增长呈指数型增长。因此，实际应用中通常使用启发式算法、近似算法或元启发式算法（如遗传算法、树搜索）来获取可接受的近似解，而不是真正的最优解。

算法介绍

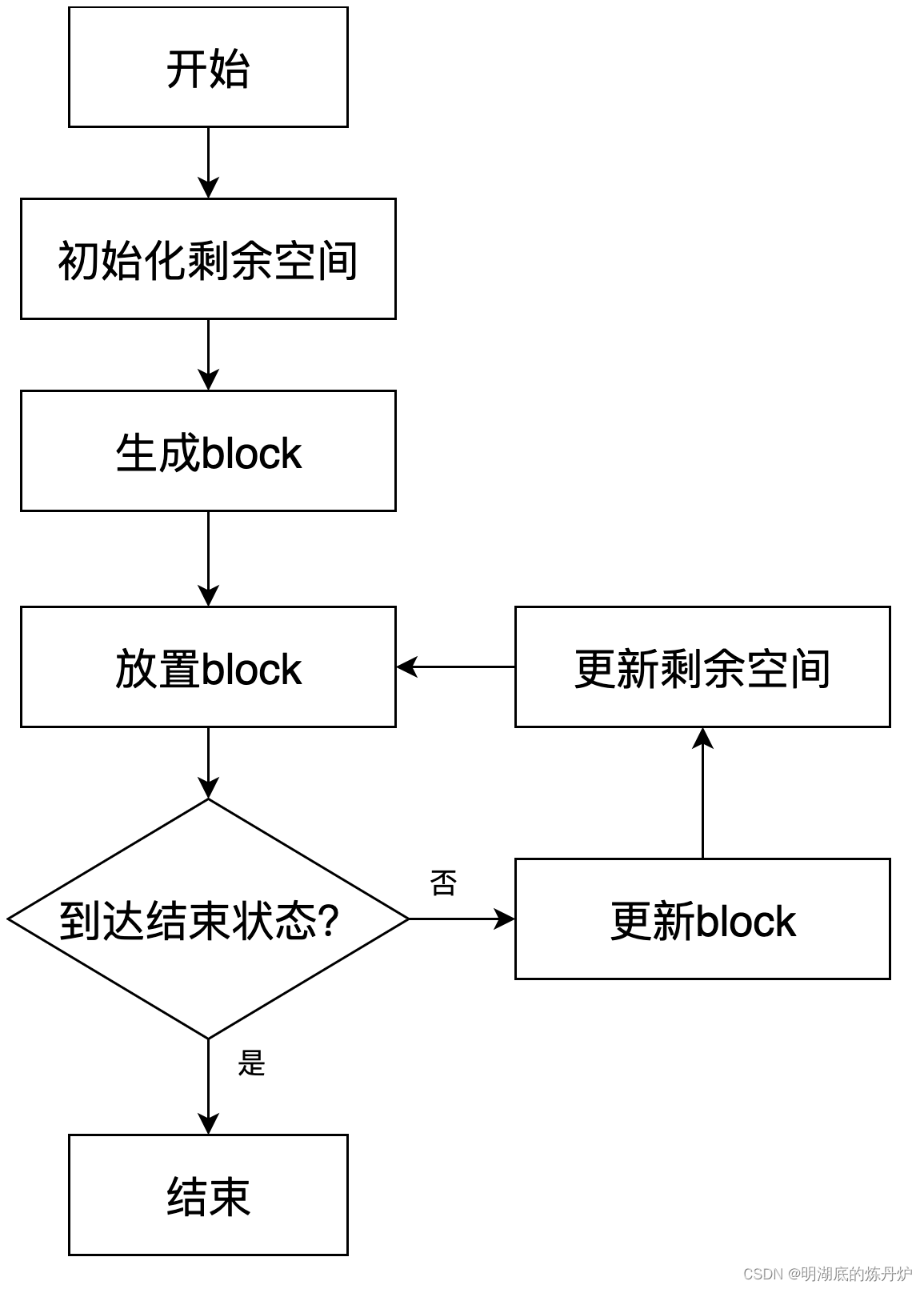
目前学术界对于三维装箱问题的主流算法是树搜索+最大剩余空间+块生成，树搜索能够在三维装箱问题极其庞大的解空间中进行合理探索，搜寻到优秀的解决方案。最大剩余空间在货物堆叠的过程中不断更新可用空间，无需每次堆叠都去判断和所有货物的位置关系。块生成算法使得装载过程更加整齐，更加迅速。在这一小节中，在这一小节中我们将着重对最大剩余空间和块生成算法进行介绍，下图为树搜索的单个节点的搜索过程。

最大剩余空间

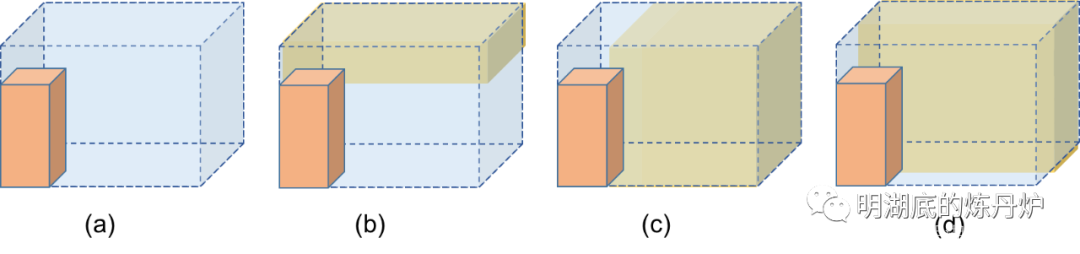
最大剩余空间是指物品在放置过程中产生的所有的可放置空间，这个空间在各自的分割方式下达到最大，可能会与别的空间重叠。以下图为例，当没有物品放入容器时，整个容器的空间即当前的最大剩余空间。按照图a讲物品放入空间之后，空间被分割图b、c、d中所示的三部分，即三个最大子空间，这样做的好处是能够产生更多放置的可能性，但是会带来额外的空间更新动作。

为了让读者更加容易理解最大剩余空间的更新过程，下图从二维的角度进一步阐述了最大子空间的划分方式，左侧深色部分表示物品占据的空间，淡色部分表示剩余空间，右侧表示划分的最大子空间。

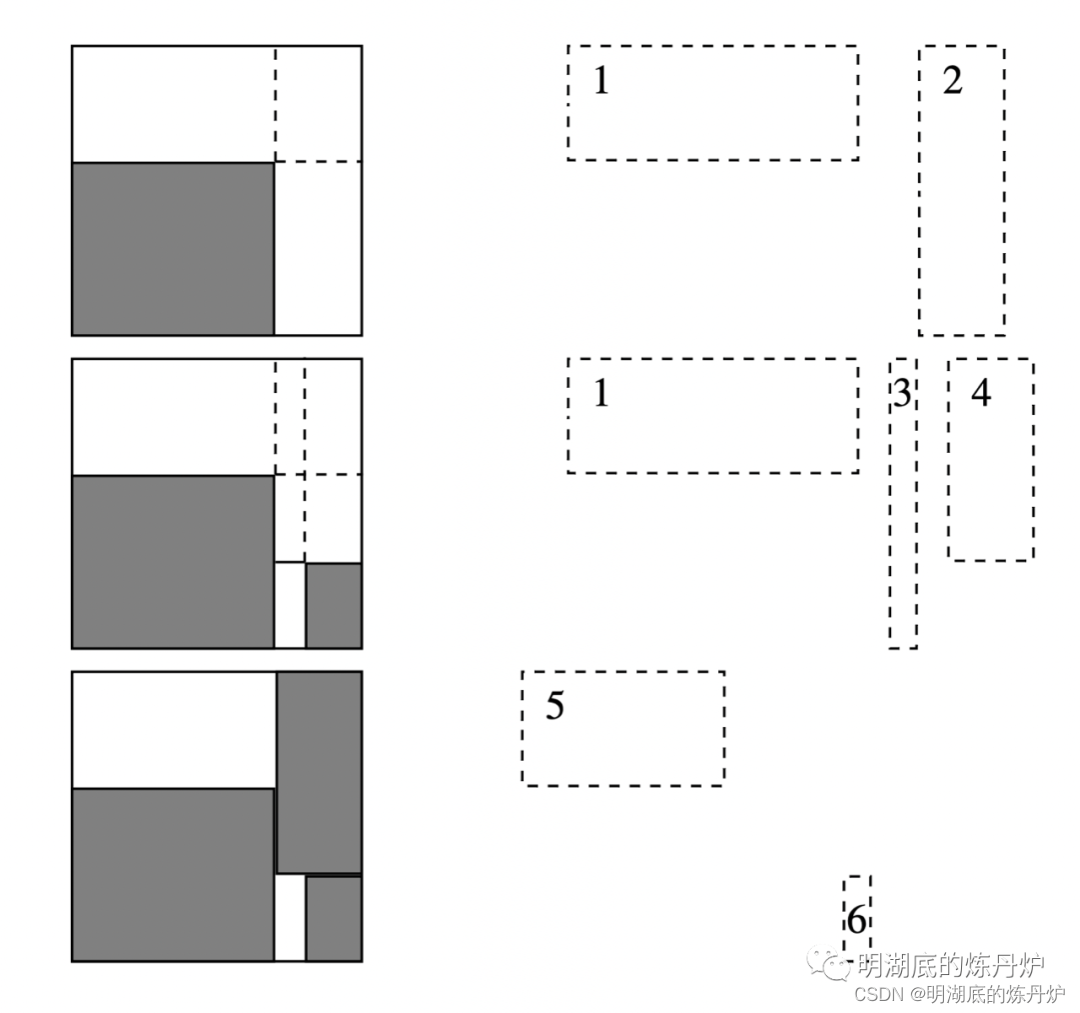
值得注意的是，由于最大子空间之间是有重叠的，因此当选定一个最大子空间并向其中放置物品时，除了更新自身的空间之外，还需要检查其余所有空间，如果物品的放置影响了该空间，则同样需要对该空间进行更新。考虑一般的情况，如下图所示，如果在空间中放入了物品，该空间将被划分成6部分，即左、右、前、后、上、下。

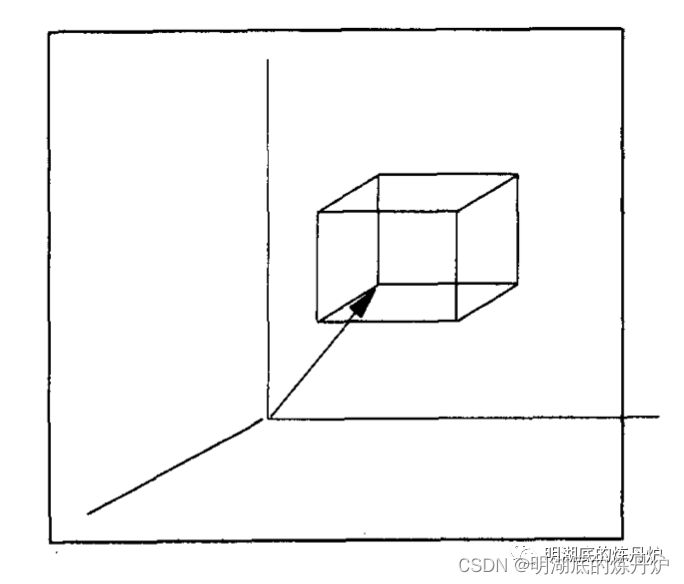
假设立方体的左下后角点坐标和右上前角点坐标分别为[x1,y1,z1]、[x2,y2,z2]，那么该立方体可以用这两个点唯一确定，表达为立方体{[x1,y1,z1],[x2,y2,z2]}。令当前空间对应的范围为{[x1,y1,z1],[x2,y2,z2]}，物品对应的范围为{[x3,y3,z3],[x4,y4,z4]}，那么空间由物品划分的空间对应为：

左侧空间：{[x1,y1,z1],[x3,y2,z2]}

右侧空间：{[x4,y1,z1],[x2,y2,z2]}

后侧空间：{[x1,y1,z1],[x2,y3,z2]}

前侧空间：{[x1,y4,z1],[x2,y2,z2]}

下侧空间：{[x1,y1,z1],[x2,y2,z3]}

上侧空间：{[x1,y1,z4],[x2,y2,z2]}

空间{[x1,y1,z1],[x2,y2,z2]}存在的充分必要条件是x2>x1且y2>y1 and z2>z1，对于不满足条件的空间，不予考虑。

块生成算法

块生成算法确实是将多个货品组合成一个单一的装载单元，即block，然后再执行装载动作。根据组合block的货品种类，这样的block可以分为single block和complex block。
Single Block
Single Block是由同一类型的货品组成的block。这些货品通常有相同的形状、尺寸和其他物理特性，这意味着它们可以很整齐地堆砌在一起，从而减少了在装载过程中可能出现的空间浪费。在处理Single Blocks时，由于货品的一致性，可采用简化的空间计算方法，使装箱过程更高效。Single Blocks是易于管理和存取的，因此它们尤其适用于需要快速装卸或高频次处理的应用场景。

Complex Block
Complex Block由不同类型的货品组合而成，每种货品可能具有不同的尺寸和形状。由于这增加了组块的复杂性，因此需要精心规划以确保块内货品的紧凑排列而不造成空间浪费。Complex Blocks通常需要使用更为复杂的规划算法，因为需要考虑每个不同货品之间的相互位置及它们的兼容性。尽管它们的创建和管理比Single Blocks复杂，Complex Blocks可以提供更好的空间利用率，尤其是在处理种类繁多的货品时。

在实际应用中，块生成算法需要解决的挑战包括：
（1）块的稳定性：无论是Single Block还是Complex Block，确保货品在运输和装载过程中的稳定性是至关重要的。这影响了货品的安全和减少损坏的可能性。

（2）空间最大化：目标是尽可能利用可用的装载空间，减少空间浪费，增加物流效率。

（3）配合装载算法：生成的块需要与装箱算法相互适应，以支持有效的装载计划和操作。

一般来说，我们更喜欢使用single block的方式来进行块生成，虽然可能在某些特定场景下complex block能够获得更好的组装方案，但是同时complex block意味着远超于simple block的block数量，这可能意味着需要更多的搜索次数，更加强大的算力支撑。另外由于simple block都是由相同的item构成的，所以simple block生成的块是紧凑的，在装载过程中能够获得更加整齐的剩余空间。

核心代码

剩余空间更新

def updateSpace(self,position3,block):
        remainSpaceCopy=deepcopy(self.remainSpace)
        
        for i in range(len(self.remainSpace)):
            space=self.remainSpace[i]
            #新增空间
            x1,y1,z1=space.position3.x,space.position3.y,space.position3.z
            x2,y2,z2=space.position3.x+space.cube.length,space.position3.y+space.cube.width,space.position3.z+space.cube.height
            x3,y3,z3=max(x1,position3.x),max(y1,position3.y),max(z1,position3.z)
            x4,y4,z4=min(x2,position3.x+block.cube.length),min(y2,position3.y+block.cube.width),min(z2,position3.z+block.cube.height)
            if self.isOverlap(space,Space(position3,block.cube,\
                Plane(Position2(space.position3.x,space.position3.y),block.cube.length,block.cube.width))):
                #删除更新空间
                remainSpaceCopy.remove(space)
                #左侧剩余空间
                planeLeft=self.getCrossPlane(space.plane,Plane(Position2(x1,y1),x3-x1,y2-y1))
                spaceLeft=Space(Position3(x1,y1,z1),Cube(x3-x1,y2-y1,z2-z1),planeLeft)
                if not spaceLeft in remainSpaceCopy and x3>x1:
                    remainSpaceCopy.append(deepcopy(spaceLeft))
                #右侧剩余空间
                planeRight=self.getCrossPlane(space.plane,Plane(Position2(x4,y1),x2-x4,y2-y1))
                spaceRight=Space(Position3(x4,y1,z1),Cube(x2-x4,y2-y1,z2-z1),planeRight)
                if not spaceRight in remainSpaceCopy and x2>x4:
                    remainSpaceCopy.append(deepcopy(spaceRight))
                #前侧剩余空间
                planeFront=self.getCrossPlane(space.plane,Plane(Position2(x1,y1),x2-x1,y3-y1))
                spaceFront=Space(Position3(x1,y1,z1),Cube(x2-x1,y3-y1,z2-z1),planeFront)
                if not spaceFront in remainSpaceCopy and y3>y1:
                    remainSpaceCopy.append(deepcopy(spaceFront))
                #后侧剩余空间
                planeRear=self.getCrossPlane(space.plane,Plane(Position2(x1,y4),x2-x1,y2-y4))
                spaceRear=Space(Position3(x1,y4,z1),Cube(x2-x1,y2-y4,z2-z1),planeRear)
                if not spaceRear in remainSpaceCopy and y2>y4:
                    remainSpaceCopy.append(deepcopy(spaceRear))
                #下侧剩余空间
                planeBelow=deepcopy(space.plane)
                spaceBelow=Space(Position3(x1,y1,z1),Cube(x2-x1,y2-y1,z3-z1),planeBelow)
                if not spaceBelow in remainSpaceCopy and z3>z1:
                    remainSpaceCopy.append(deepcopy(spaceBelow))
                #上侧剩余空间
                planeAbove=Plane(Position2(x3,y3),x4-x3,y4-y3)
                spaceAbove=Space(Position3(x1,y1,z4),Cube(x2-x1,y2-y1,z2-z4),planeAbove)
                if not spaceAbove in remainSpaceCopy and z2>z4:
                    remainSpaceCopy.append(deepcopy(spaceAbove))
                    
        remainSpaceCopy.sort(key=functools.cmp_to_key(self.spaceCmp1))
        return remainSpaceCopy

简单块生成

def genSimpleBlock(self,space,items):
        blockTable=[]
        L,W,H=space.cube.length,space.cube.width,space.cube.height
        for k in items:
            item=items[k]
            num=item.num
            for direction in item.feasibleDirection:
                find=False
                cube=item.rotateCube(direction)
                l,w,h=cube.length,cube.width,cube.height
                if l<=L and w<=W and h<=H:
                    for i in range(num,0,-1):
                        for j in range(int(num/i),0,-1):
                            for k in range(int(num/i/j),0,-1):
                                if i*l>L or j*w>W or k*h>H:
                                    continue
                                block=Block()
                                block.getBlockDetail(item,direction,i,j,k,'')
                                position3=self.getPutPosition3(block,space)
                                if not type(position3)==type(None):
                                    find=True
                                    block.position3=deepcopy(position3)
                                    blockTable.append(block)
                                    break
        blockTable.sort(key=functools.cmp_to_key(self.blockCmp))
        return blockTable

结果展示

装载范围约束
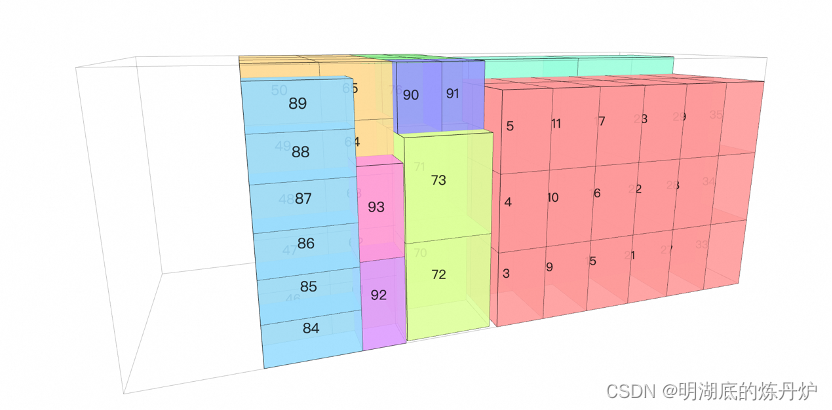
货物只能在指定范围内进行装载，可以在容器中预留空间，预留的空间可以通过ax+by+cz+d<=0的任意凸平面表达，且可以存在多个预留空间。

货物支撑约束
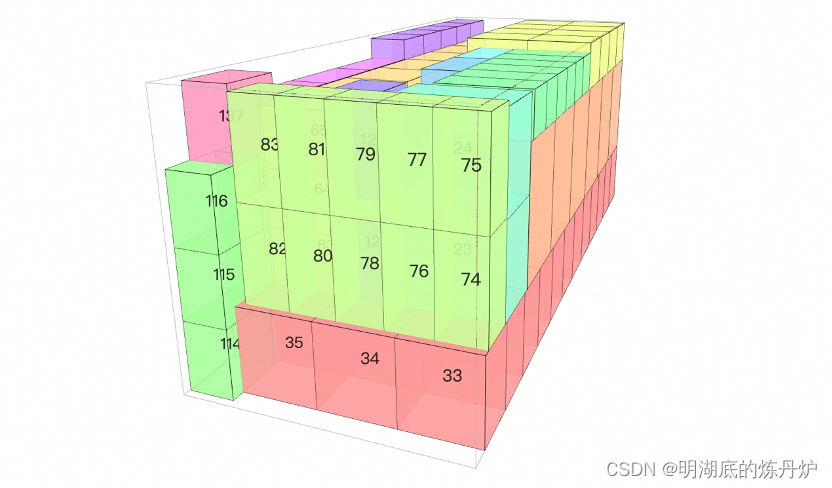
所有货物都需要被容器或者其他货物支撑，支撑比例支持自定义，例如0.5表示当前放置方向下货品至少有50%的底面面积要被容器或者其他货物支撑。

重心约束
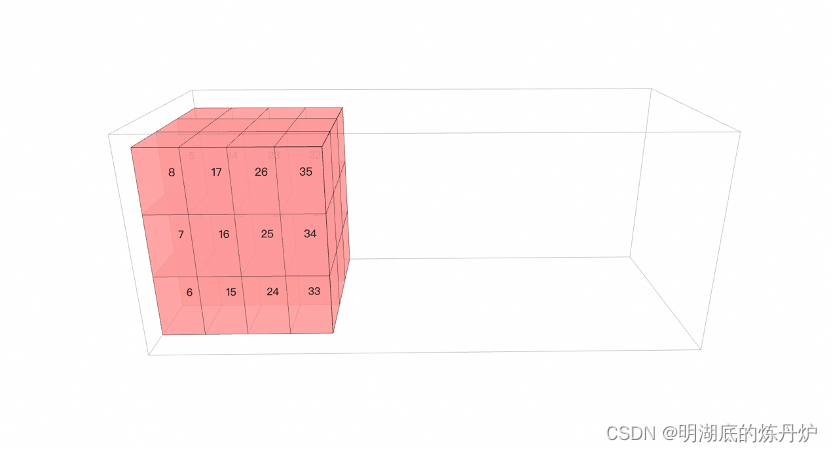
货物装载保证满足最大重心偏移量，在装载过程中综合考虑转载率和重心满足的可能性，获得装载方案后，如果重心不满足偏移条件，代码支持对货物位置进行调整，以获得可行的装载方案。


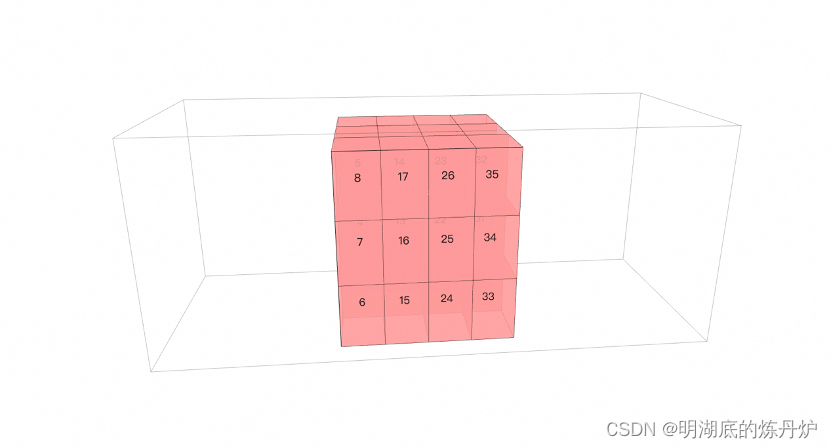
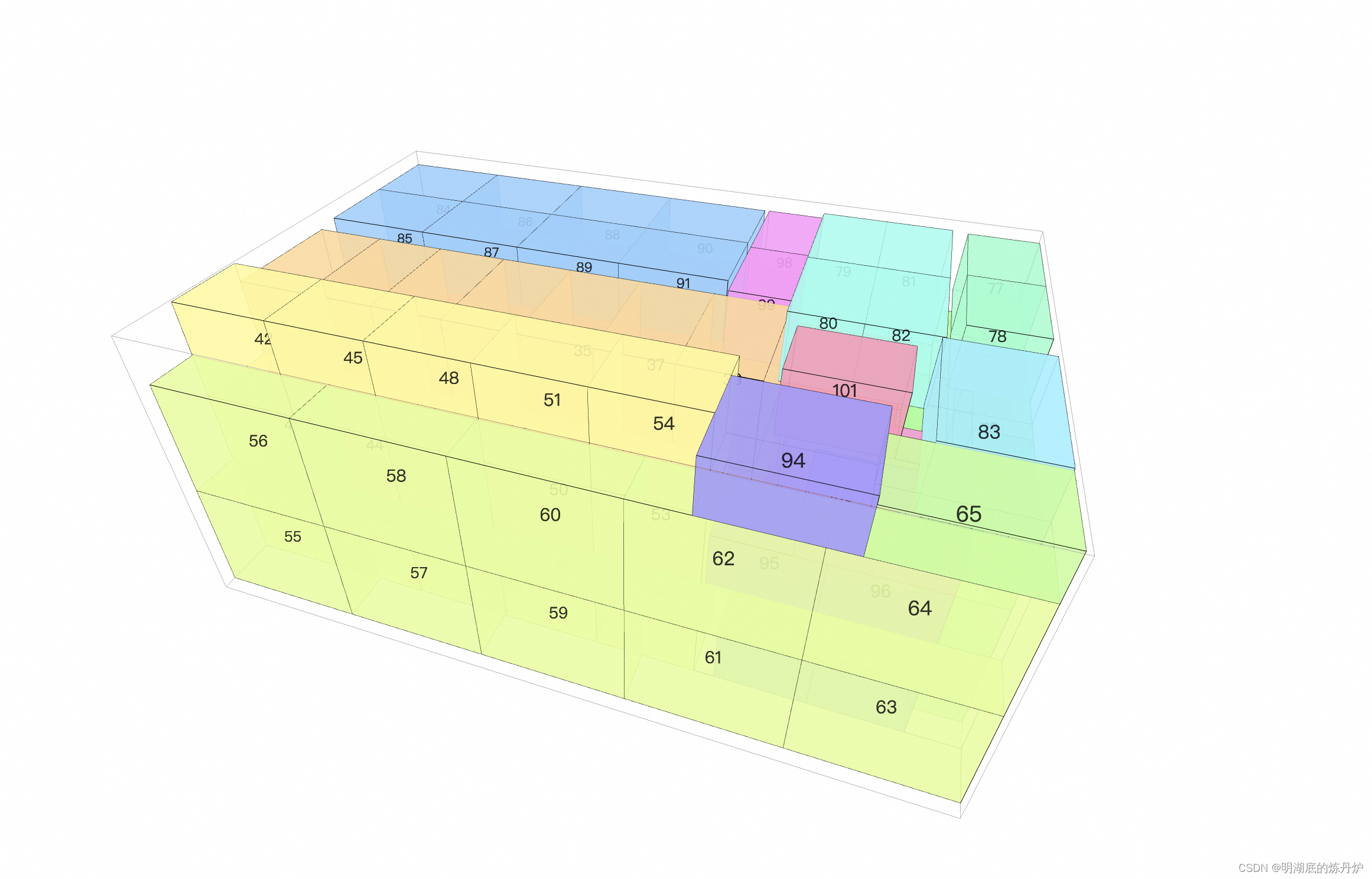
结果输出
结果输出包含两部分，一部分是结果概览，另一部分是放置详情。结果概览包括转载方案的装载重量、体积、重心位置等，放置详情中则详细地罗列了每个货品的具体放置位置以及放置方向。

{'loadVolume': 32182127200, 'remainVolume': 3637916000, 'loadWeight': 19410, 'fillRate': 0.9089634369867572, 'gravityCenter': (2895.122102007782, 1373.7403400302042)}

[{'position': [0, 0, 0], 'cube': [1320, 1180, 782], 'code': '0'},
{'position': [0, 0, 782], 'cube': [1320, 1180, 782], 'code': '0'}, 
{'position': [1320, 0, 0], 'cube': [1320, 1180, 782], 'code': '0'}, 
{'position': [1320, 0, 782], 'cube': [1320, 1180, 782], 'code': '0'}, 
{'position': [2640, 0, 0], 'cube': [1320, 1180, 782], 'code': '0'}]

本文小节

本文简单介绍了三维装箱问题的主流算法框架以及最大剩余空间和列生成的基本实现方法，并且简单介绍了三维装箱问题中的一些常见约束。三维装箱是一个相对复杂又应用广泛的组合优化问题，本文只是做简单介绍，若想在应用在实际项目中，还有很多优化技巧，本文不一一展开。