---

1.组合总和 Ⅳ

1.题目链接

• 组合总和 Ⅳ

---

2.算法原理详解

• 本题是个排列题，而并非组合题，所以并非背包问题
• • 思路：

    • 确定状态表示：根据分析问题的过程中，发现重复子问题，抽象出来一个状态表示

      • dp[i]：凑成总和为i，一共有多少种排列数

    • 推导状态转移方程

      • dp[i] += dp[i - nums[j]]
        

    • 初始化：dp[0] = 1

    • 确定填表顺序：从左往右

    • 确定返回值：dp[target]

---

3.代码实现

int combinationSum4(vector<int>& nums, int target) 
{
    vector<unsigned long long> dp(target + 1);
    dp[0] = 1;

    for(int i = 1; i <= target; i++)
    {
        for(auto& x : nums)
        {
            if(i >= x)
            {
                dp[i] += dp[i - x];
            }
        }
    }

    return dp[target];
}

---

2.不同的二叉搜索树

1.题目链接

• 不同的二叉搜索树

---

2.算法原理详解

• 思路：

  • 确定状态表示：根据分析问题的过程中，发现重复子问题，抽象出来一个状态表示

    • dp[i]：结点个数为i的个时候，一共有多少种二叉搜索树

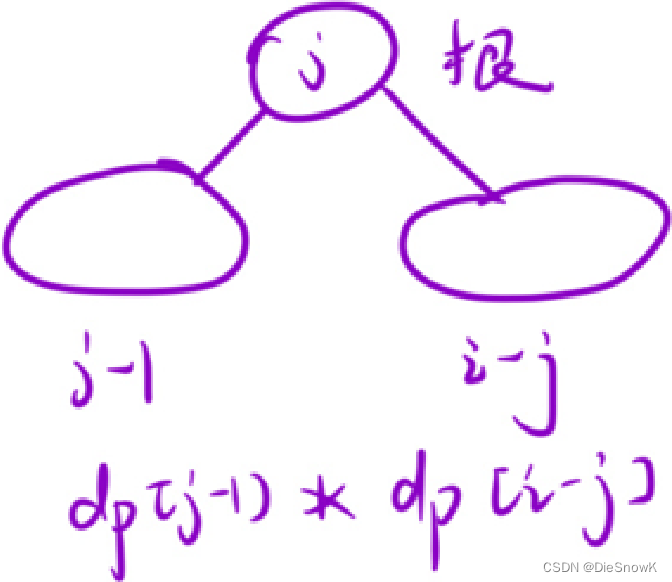
  • 推导状态转移方程

    • dp[i] += dp[j - 1] * dp[i - j]
      

  • 初始化：dp[0] = 1

  • 确定填表顺序：从左往右

  • 确定返回值：dp[n]

---

3.代码实现

int numTrees(int n) 
{
    vector<int> dp(n + 1);
    dp[0] = 1;

    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= i; j++)
        {
            dp[i] += dp[i - j] * dp[j - 1];
        }
    }

    return dp[n];
}