树的概念
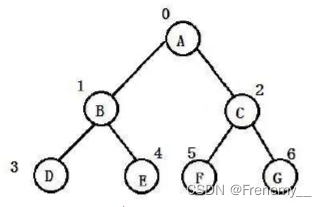
树是一种非线性的数据结构,它是由n个有限节点组成一个具有层次关系的集合,它看起来像棵树,所以称其为“树”。如下图:

树可以分为根和子树,而子树又可以被分为根和子树,故我们可以用递归对其进行实现。
注意:子树之间不能相交
树的实现
1.顺序表
可以用结构体设置TreeNode再用顺序表存子树,代码如下:
struct TreeNode
{
int val;
SeqList subs;
vector<struct TreeNode*> subs;
};2.左孩子右兄弟
定义两个指针:孩子指针,兄弟指针。图示如下:

无论父亲有多少孩子,都只用指向后代第一个孩子,接下来的每个孩子都向右指向兄弟。
像这样设计,若想要遍历时则比较方便。
struct TreeNode
{
int val;
struct TreeNode* leftchild;
struct TreeNode* rightbrother;
};二叉树
二叉树是数据结构中非常重要的一个算法.
二叉树的概念
一颗二叉树是节点的一个有限结合,该集合或为空,或为由一个节点加上两棵树(分别称为左子树和右子树)组成。
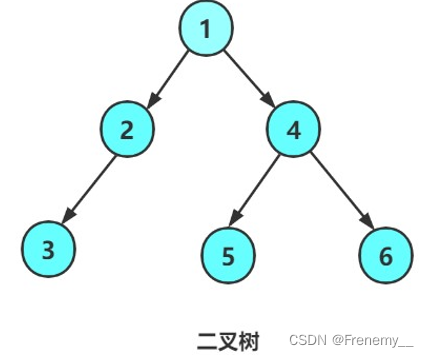

满二叉树
一个二叉树,如果每一个层的结点数都达到大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为且结点总数是,则它就是满二叉树。
完全二叉树
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为的,有n个节点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至N的节点,即称为二叉树,要注意的是满二叉树是一种特殊的完全二叉树。
完全二叉树的结构
我们这里用数组来储存二叉树中的数据
逻辑结构(想象出来的)
我们想象它是这样存的
物理结构(计算机中实际存储的)
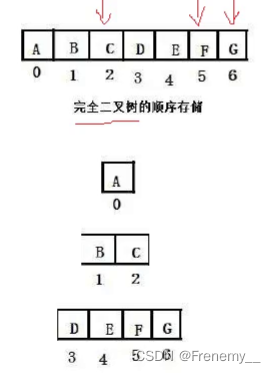
由此我们可以推出:
假设父亲在数组中的下标为i,则左孩子在数组中的下标是:2*i+1;右孩子在数组中的下标是2*i+2(仅对于完全二叉树和满二叉树成立).
所以我们发现对于这种数组存储会造成内存浪费,所以只适合完全二叉树。