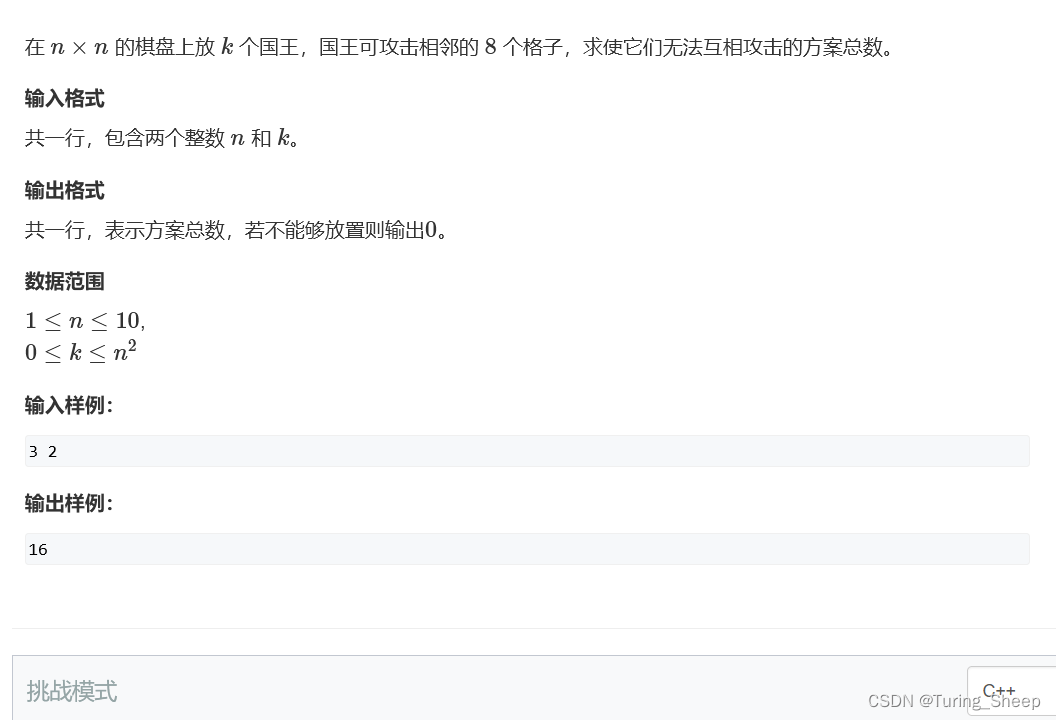
一、问题

二、思路

1、整体逻辑

我们看下面这个例子：

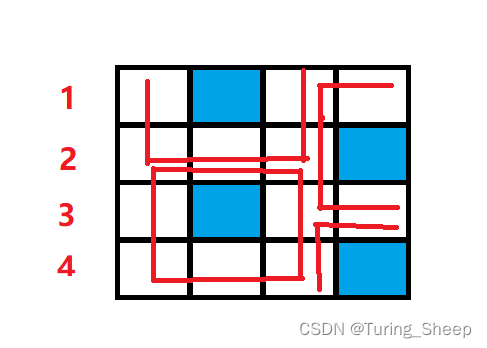
如果我们一行一行放的话。

在上图中，我们先看第二行，我们发现第二行在哪个位置可以放置国王，完全取决于第一行如何放的。而我们在第二行放了国王后，第二行的国王不仅会影响本层其余国王的放置，还会影响第三行国王的放置。

但是大家可能会疑惑，第二行明明也影响到了第一行，难道第二行放置了国王后，第一行的国王不会受影响吗？

答案是不会的，假设第二行的国王影响到了第一行的国王，那么说明第一行的某个国王在第二行某个国王的范围内，同理此时第二行的该国王也在第一行该国王的范围内，此时说明第二行放置的这个国王也是不合法的，而我们在放置第二行国王的时候就已经避开了第一行国王的范围，所以不会出现这种情况。

从上面的分析我们可以得出结论，第i行如何放置国王，取决于第i-1行是如何放置的。

那么怎样才算合法呢？

我们采用状态压缩的方式，放置国王标1，不放标0，最后组成一个二进制数A和B。

那么针对这两个A和B，满足下列要求的时候才算是合法的。

2、状态表示

$f[i][j][s]$表示在前$i$行中放置国王，共放置$j$个国王的情况下，且第$i$行的状态是j的时候，所有的方案总数。

3、状态转移

根据一开始的分析，第i行如何放置国王取决于第$i-1$行的国王放置情况，因此，我们按照第$i-1$行的不同状态来写不同的方程。
$$f[i][j][s]=\sum f[i-1][j-count(s)][ss]$$
其中$count(ss)$代表状态$s$下第$i$行中放置了多少个国王。因为第$i$行放置$count(s)$个，前$i-1$行只能放置$j-count(s)$个。

4、循环设计

首先我们需要去枚举i和j，这个是比较简单的。由于我们是按照第i-1行分类的，所以我们还需要枚举第i-1中所有的可能合法的状态，接着再去根据其中的某个状态计算第i行可能合法的状态。
所以总共需要4层循环。

有人会问这个会不会超时，其实我们可以先把对于一行而言所有合法的状态存储下来，即把那些二进制中1不相邻的状态存储下来，其实经过计算满足这个条件的状态最多有144个。我们可以估算为200。
而n的最大值是10，国王个数的最大值是100，那么时间复杂度就是200 * 200 * 10 * 100=4 * 10⁷这完全是能够算完的。

5、初末状态

这个比较简单，f[0][0][0]初始化为1即可。
最后的状态是f[n+1][m][0]，即第n+1行不放国王，总共放了m个国王的总方案数。

三、代码

#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
const int N=15,K=110,S=1<<10;
long long f[N][K][S];
int n,m;
vector<int>state;
vector<int>st[S];

bool check(int x)
{
    for(int i=0;i+1<n;i++)
    {
        if((x>>i&1)&&(x>>(i+1)&1))return false;
    }
    return true;
}

int get_nums(int x)
{
    int res=0;
    for(int i=0;i<n;i++)
        res+=x>>i&1;
    return res;
}

int main()
{
    cin>>n>>m;
    for(int i=0;i<1<<n;i++)//记录所有对于本行而言合法的状态
        if(check(i))state.push_back(i);
        
    f[0][0][0]=1;
    
    for(int i=1;i<=n+1;i++)//枚举i
    {
        for(int j=0;j<=m;j++)//枚举j
        {
            for(int ss=0;ss<state.size();ss++)//枚举第i-1行的状态
            {
                for(int s=0;s<state.size();s++)//枚举第i行的状态
                {
                    if(!(state[ss]&state[s])&&(check(state[ss]|state[s])))//判断两行之间是否合法
                    {
                        int count=get_nums(state[s]);//计算第i行的国王数目
                        if(j>=count)
                        {
                            f[i][j][state[s]]+=f[i-1][j-count][state[ss]];
                        }
                    }
                }
            }
        }
    }
    cout<<f[n+1][m][0]<<endl;
    return 0;
}