“编辑距离”系列总结，一文读懂（Java实现）

news2024/9/23 13:27:15

目录

一、判断子序列 ——>删除元素

1.1、dp定义

1.2、递推公式

1.3、初始化

1.4、遍历顺序

1.5、解题代码

二、不同的子序列 ——>删除元素

2.1、dp定义

2.2、递推公式

2.3、初始化

2.4、遍历顺序

2.5、解题代码

三、两个字符串的删除操作 ——>删除元素

3.1、dp定义

3.2、递推公式

3.3、初始化

3.4、遍历顺序

3.5、解题代码

四、编辑距离 ——>删除、增加、替换元素

4.1、dp定义

4.2、递推公式

4.3、初始化

4.4、遍历顺序

4.5、解题方程

小结

一、判断子序列 ——>删除元素

题目描述：

题目来源：392. 判断子序列

1.1、dp定义

 分析：

        判断s是否为t的子序列，实际上就是在求s和t的最长公共子序列的长度是否和s的长度相等，这个问题也是“编辑距离”中的一个入门级别的题目。

如果对最长公共子序列不太理解的，可以看看这篇：

http://t.csdn.cn/DAaaK

dp定义：

dp[i][j]表示字符串s以i - 1为结尾，字符串t以j - 1为结尾的最长公共子序列的长度。

建议：对于两个字符串要比较相同字符的情况，都最好定义成以i - 1，j - 1结尾~

1.2、递推公式

分析：

dp[i][j]就表示最长公共子序列的长度，我们该怎么推出他呢？

1.当s[i] - 1 == t[i - 1]时， 说明当前这对字符相等，如下：

那么dp[i][j]就等于s和t相同的这个字符前面这一段最长公共子序列 + 1得到，+1就表示s和t的当前对比的字符相等，所以在原来的基础上dp[i - 1][j - 1]进行+1操作，如下：

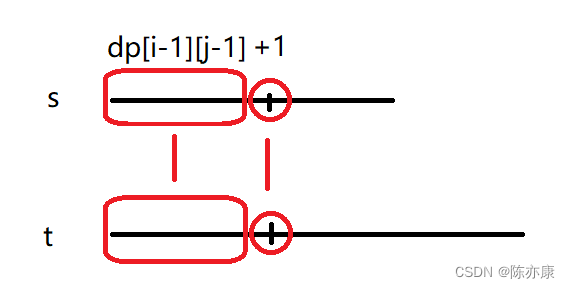
2.当s[i] != t[i]时，说明当前这对字符不相等，那么就不进行+1操作，那么当前状态dp[i][j]就可以由dp[i][j - 1]来进行表示，相当于删除了t的一个字符，让s的第i - 1和t的第j - 2个元素比较，而dp[i][j - 1]这个状态，我们在上一次的递推已经的出来了，所以可以直接拿来用；

递推公式：

if(s.charAt(i - 1) == t.charAt(j - 1)) { 

        dp[i][j] = dp[i - 1][j - 1] + 1;

} else {

        dp[i][j] = dp[i][j - 1];

}

1.3、初始化

分析：

之前我们将dp数组定义成i - 1和j - 1，为什么不是i,j呢？原因就在初始化这里！

        若定义成i,j，假设我们定义成以i为结尾，初始化的时候nums[i][0]和nums[0][j]该怎么初始化？dp[i][0]就是“nums1以nums1[i]为结尾，nums2以nums2[0]为结尾的最长子数组”，那么我们就需要揪住nums2[0]这个元素去遍历nums1这个数组，去统计相同的元素，同理，nums[0][j]也是如此！

        但如果我们定义成i - 1, j - 1，nums[i][0]这里的0 - 1就是-1，相当于空串，空串的最长公共子序列自然是0，所以直接初始化成0即可；dp数组中其他元素初始化成什么都可以，因为在递推的过程中都会被覆盖。

1.4、遍历顺序

        由递推公式可以知道，推出dp[i][j]都是需要前一个元素，所以只需要从上到下，从左往右遍历即可~

1.5、解题代码

class Solution {
    public boolean isSubsequence(String s, String t) {
        int len1 = s.length();
        int len2 = t.length();
        int[][] dp = new int[len1 + 1][len2 + 1];
        for(int i = 1; i <= len1; i++) {
            for(int j = 1; j <= len2; j++) {
                if(s.charAt(i - 1) == t.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = dp[i][j - 1];
                }
            }
        }
        return dp[len1][len2] == s.length();
    }
}

二、不同的子序列 ——>删除元素

题目描述：

题目来源：115. 不同的子序列

2.1、dp定义

分析：

按照之前的套路， 对于两个字符串要比较相同字符的情况，定义成以i - 1，j - 1结尾即可。

定义：

dp[i][j]表示以字符串s的第i - 1个字符为结尾，以字符串t的第j - 1个字符为结尾，s的子序列中t的个数。

2.2、递推公式

分析：

1.当s[i - 1] == t[j - 1]时，就不用考虑当前i-1,j-1为结尾表示的字符了，也就是考虑i-2,j-2为结尾的个数dp[i - 1][j - 1]，因为这个状态之前已经推出，直接拿来用即可，如下：

dp[i][j] = dp[i - 1][j - 1]就完了吗？实际上我们这里写的s[i - 1]表示是否要考虑这个元素，以上是考虑这个元素，那么不考虑又是怎么回事呢？如下：

为什么不考虑dp[i][j - 1]呢？因为本题求的是从s的子序列中有多少个t！

 2.当s[i - 1] != t[j - 1]时，就删掉s一个元素，考虑s的以s[i - 2]为结尾的序列即可。

递推公式：

if(s.charAt(i - 1) == t.charAt(j - 1)) {

        dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];

} else {

        dp[i][j] = dp[i - 1][j];

}

2.3、初始化

分析：

从递推公式中可以看出，一直往前递推，找到根源就是需要知道dp[i][0]和dp[0][j]。

dp[i][0]表示s以i - 1为结尾，t以0 - 1为结尾，s的子序列中t的个数。

那么t就相当于是空串，s的子序列中有几个空串呢？当把s中所有的字符都删除掉，就是一个空串了，因此dp[i][0] = 1；

dp[0][j]表示s以0 - 1为结尾，t以j - 1为结尾，s的子序列中t的个数。

这里无论s本身就是一个空串了，就更别谈子序列了，也就是说s无论怎么删，t都不可能等于s，除非t也是空串，因此dp[j][0] = 0，dp[0][0] = 1;

初始化：

 dp[i][0] = 1；

dp[j][0] = 0；

dp[0][0] = 1；

2.4、遍历顺序

由递推公式可以知道，只有从以下几个方面可以得到dp[i][j]：

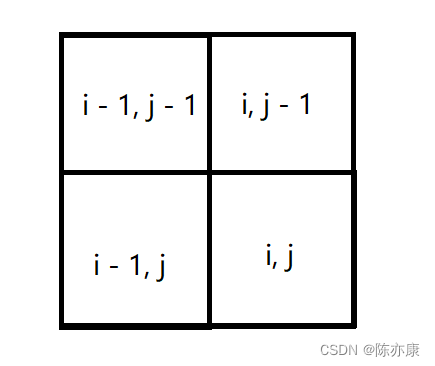
因此遍历顺序因该是从上往下，从左往右。

2.5、解题代码

class Solution {
    public int numDistinct(String s, String t) {
        int len1 = s.length();
        int len2 = t.length();
        int[][] dp = new int[len1 + 1][len2 + 1];
        //初始化
        for(int i = 0; i <= len1; i++) {
            dp[i][0] = 1;
        }
        //递推
        for(int i = 1; i <= len1; i++) {
            for(int j = 1; j <= len2; j++) {
                if(s.charAt(i - 1) == t.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[len1][len2];
    }
}

三、两个字符串的删除操作 ——>删除元素

题目描述：

题目来源：583. 两个字符串的删除操作 

3.1、dp定义

分析：

        对于两个字符串要比较相同字符的情况，都最好定义成以i - 1，j - 1结尾（如果不明白，建议看看上面几道题的讲解，已经说的很清楚了），dp[i][j]就定义成最终问题的解即可。

dp定义：

dp[i][j]：字符串word1以i - 1为结尾，字符串word2以j - 1为结尾的，使两字符串相同的最小步数。

3.2、递推公式

分析：

1.当w1[i - 1] == w2[j - 1]时，也就是当前对比的两个字符相等时，说明不需要进行删除操作，就可以先忽略这对字符，用这一对字符前面的字符串（dp[i - 1][j - 1]）表示使字符串相同的最小步数即可。

2.当w1[i - 1] != w2[j - 1]时，也就是当前对比的两个字符不相等时，说明需要进行删除操作，这时候就需要考虑到底是删w1[i - 1]合适（删除后，比较之前进行删除操作的步骤更少）还是删w2[j - 1]合适，那么这时候就需要看dp[i - 1][j]和dp[i][j - 1]谁更小，比较删除当前字符后，对比之前进行删除操作的步骤谁更少，最后再+1，表示删除当前字符这个步骤。

递推公式：

if(word1.charAt(i - 1) == word2.charAt(j - 1)) {

        dp[i][j] = dp[i - 1][j - 1];

} else {

        dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + 1;

}

3.3、初始化

分析：

        从递推公式中可以看出，要初始化 dp[i - 1][j - 1]、dp[i - 1][j]、dp[i][j - 1] 一直往前递推，找到根源就是需要知道dp[i][0]和dp[0][j]。

1.dp[i][0]表示w1以i - 1为结尾，w2以0 - 1为结尾，使w1和w2相同的最小步数。

也就是说w2是一个空串，通过删除w1的字符，使两个字符串相等，具体的，如下图：

2.dp[0][j]同理。

初始化：

for(int i = 0; i <= len1; i++) {

        dp[i][0] = i;

}

for(int j = 0; j <= len2; j++) {

        dp[0][j] = j;

}

3.4、遍历顺序

 由递推公式可以知道，只有从以下几个方面可以得到dp[i][j]：

因此遍历顺序因该是从上往下，从左往右。

3.5、解题代码

class Solution {
    public int minDistance(String word1, String word2) {
        int len1 = word1.length();
        int len2 = word2.length();
        int[][] dp = new int[len1 + 1][len2 + 1];
        for(int i = 0; i <= len1; i++) {
            dp[i][0] = i;
        }
        for(int j = 0; j <= len2; j++) {
            dp[0][j] = j;
        }
        for(int i = 1; i <= len1; i++) {
            for(int j = 1; j <= len2; j++) {
                if(word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + 1;
                }
            }
        }
        return dp[len1][len2];
    }
}

四、编辑距离 ——>删除、增加、替换元素

Ps：建议理解了上面讲解的三道题，再来看这道题，就不难掌握了~

题目描述：

题目来源：72. 编辑距离

4.1、dp定义

分析：

        对于两个字符串要比较相同字符的情况，都最好定义成以i - 1，j - 1结尾（如果不明白，建议看看上面几道题的讲解，已经说的很清楚了），dp[i][j]就定义成最终问题的解即可。

dp定义：

dp[i][j]：字符串w1以i - 1为结尾，字符串w1以j - 1为结尾，w1转化成w2的最少操作次数。

4.2、递推公式

分析：

1.当前对比的这对字符相同时，就不用进行任何的编辑操作（增加、删除、替换），也就是说可以忽略这对字符，直接用这对 字符 前面的 字符串的状态（dp[i - 1][j - 1]）来表示当前状态dp[i][j]；

2.当前对比的这对字符不相同时，想要让w1转化成w2，可以对字符进行增加、删除、替换的操作，最后从这些操作中选出一个操作次数最少的来表示dp[i][j]，具体的：

1) 增加、删除元素

        先来谈谈删除元素，当前这对字符不相同，我们因该考虑的是删除w1[i]还是w2[j]这个字符合适，怎么才算合适？就要看忽略（这里的忽略就是删除操作）了w1[i]（忽略后的状态为dp[i - 1][j]，w1以i - 2为结尾，w2以j - 1为结尾的最小编辑距离）或w2[j]（忽略后的状态为dp[i][j - 1]）以后，谁的编辑距离要更小！最后再+1，这个+1就表示删除元素这一步的操作，最后就得到了dp[i][j]这个状态。

        那么增加元素呢？实际上，增加和删除元素的转移方程是一样的，因为站在w1的角度来删除自身的元素，站在w2的角度看就是在增加自己的元素，如下图：

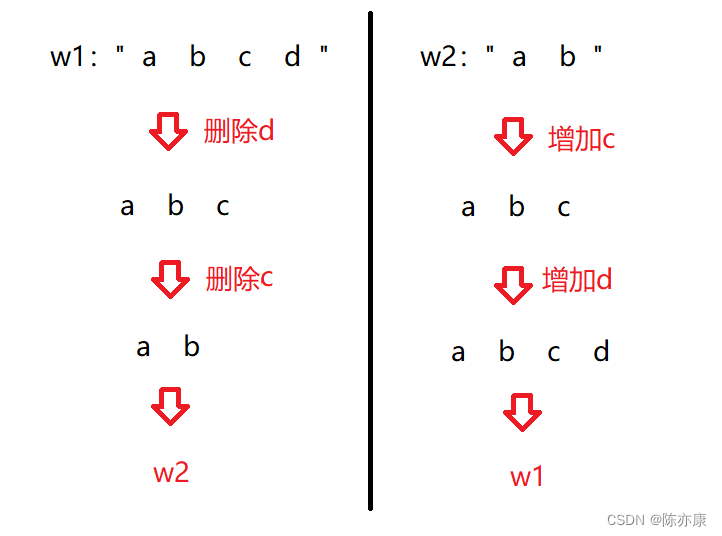
2)替换元素

        替换元素就是在dp[i -1][j - 1]这个状态的基础上，通过替换，使下一对字符相等的一个操作！也就是说，替换就是为了当前这对元素相等，在dp[i - 1][j - 1]这个状态上通过一个+1（+1就是替换）的操作，使下一对字符变成相等。

状态转移方程：

if(word1.charAt(i - 1) == word2.charAt(j - 1)) {
    dp[i][j] = dp[i - 1][j - 1];
} else {
    //增加删除
    int addDel = Math.min(dp[i - 1][j], dp[i][j - 1]) + 1;
    //替换
    int replace = dp[i - 1][j - 1] + 1;
    dp[i][j] = Math.min(addDel, replace);
}

4.3、初始化

分析：

        从递推公式中可以看出，要初始化 dp[i - 1][j - 1]、dp[i - 1][j]、dp[i][j - 1] 一直往前递推，找到根源就是需要知道dp[i][0]和dp[0][j]。

1.dp[i][0]表示w1以i - 1为结尾，w2以0 - 1为结尾，使w1和w2相同的最小编辑距离

也就是说w2是一个空串，通过删除w1的字符或增加w2的字符，使两个字符串相等，具体的，如下图：

 

2.dp[0][j]同理。

初始化：

for(int i = 0; i <= len1; i++) {

        dp[i][0] = i;

}

for(int j = 0; j <= len2; j++) {

        dp[0][j] = j;

}

4.4、遍历顺序

由递推公式可以知道，只有从以下几个方面可以得到dp[i][j]：

因此遍历顺序因该是从上往下，从左往右。

4.5、解题方程

class Solution {
    public int minDistance(String word1, String word2) {
        int len1 = word1.length();
        int len2 = word2.length();
        int[][] dp = new int[len1 + 1][len2 + 1];
        //初始化
        for(int i = 0; i <= len1; i++) {
            dp[i][0] = i;
        }
        for(int j = 0; j <= len2; j++) {
            dp[0][j] = j;
        }
        //递推
        for(int i = 1; i <= len1; i++) {
            for(int j = 1; j <= len2; j++) {
                if(word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    //增加删除
                    int addDel = Math.min(dp[i - 1][j], dp[i][j - 1]) + 1;
                    //替换
                    int replace = dp[i - 1][j - 1] + 1;
                    dp[i][j] = Math.min(addDel, replace);
                }
            }
        }
        return dp[len1][len2];
    }
}

小结

面试遇到，还不得装一装（doge）

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/181658.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

设计模式 - 六大设计原则之DIP（依赖倒置原则）

设计模式 - 六大设计原则之DIP（依赖倒置原则）

文章目录概述CaseBad ImplBetter Impl概述 设计代码架构时&#xff0c;高层模块不应该依赖于底层模块&#xff0c;二者都应该依赖于抽象。 抽象不应该依赖于细节&#xff0c;细节应该依赖于抽象。 依赖倒置原则是实现开闭原则的重要途径之一&#xff0c; 它降低了类之间的耦合…
阅读更多...
代码随想录算法训练营第十天 | 理论基础，232.用栈实现队列，225. 用队列实现栈

代码随想录算法训练营第十天 | 理论基础，232.用栈实现队列，225. 用队列实现栈

一、参考资料理论基础文章讲解&#xff1a;https://programmercarl.com/%E6%A0%88%E4%B8%8E%E9%98%9F%E5%88%97%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html 用栈实现队列题目链接/文章讲解/视频讲解&#xff1a;https://programmercarl.com/0232.%E7%94%A8%E6%A0%88%E5%AE%9E%E…
阅读更多...
【Linux】多线程详解（上）

【Linux】多线程详解（上）

&#x1f387;Linux&#xff1a; 博客主页&#xff1a;一起去看日落吗分享博主的在Linux中学习到的知识和遇到的问题博主的能力有限&#xff0c;出现错误希望大家不吝赐教分享给大家一句我很喜欢的话&#xff1a; 看似不起波澜的日复一日&#xff0c;一定会在某一天让你看见坚持…
阅读更多...
百度2015年系统工程师笔试题：判断当前机器的大小端

百度2015年系统工程师笔试题：判断当前机器的大小端

本篇文章主要讲解大小端的判断问题&#xff0c;需要拥有指针&#xff0c;位段&#xff0c;联合体的知识。 目录 一.题目呈现 二.三种解题方法 1.巧妙利用指针和强制转换 2.利用位段的特性 3.利用联合体的性质 一.题目呈现 请简述大端字节序和小端字节序的概念&#xff0c;…
阅读更多...
剑指 Offer 03. 无重复字符的最长子串 [C语言]

剑指 Offer 03. 无重复字符的最长子串 [C语言]

目录题目思路1代码1结果1思路2代码2结果2该文章只是用于记录考研复试刷题题目 Leetcode 03: 给定一个字符串 s &#xff0c;请你找出其中不含有重复字符的 最长子串 的长度。 示例 1: 输入: s “abcabcbb” 输出: 3 解释: 因为无重复字符的最长子串是 “abc”&#xff0c;所…
阅读更多...
A股上市公司招投标数据

A股上市公司招投标数据

一、数据简介 招投标是指在市场经济条件下进行大宗货物的买卖、工程建设项目的发包与承包以及服务项目的采购与提供时所采取的一种普遍交易方式。招标和投标是一种商品交易行为&#xff0c;是交易过程的两个方面。历经三十多年的发展&#xff0c;我国已经形成了覆盖全国各领域、…
阅读更多...
Java类和对象的学习笔记

Java类和对象的学习笔记

本篇介绍了面向对象和面向过程的关系,类的定义,对象的成员(成员变量,成员方法)和对象成员访问,类和对象的关系 对象的初始化,对象的构造(构造方法的定义和使用),对象内的this介绍和用法… 细节较多.建议收藏,看完此篇,踏上面向对象的第一步~ 类和对象的学习一.初识面向对象1.什…
阅读更多...
一文读透JVM虚拟机结构[迭代中]

一文读透JVM虚拟机结构[迭代中]

注: 码字辛苦, 转载请标注转载来源 jvm结构图: [1] 整个JVM架构包含三部分: 类加载 加载 双亲委派机制 链接 初始化 静态变量的初始值赋值 运行时数据区域 线程私有区域线程共享区域 执行引擎 解释器JIT即时编译器GC 运行时数据区域 线程私有区域: 线程私有区域主…
阅读更多...
Springboot整合分布式链路追踪SkyWalking之探针使用和链路采集实战(二)

Springboot整合分布式链路追踪SkyWalking之探针使用和链路采集实战(二)

目录 1.链路追踪-框架Springboot项目搭建 1.1 创建一个Springboot项目 1.2 SpringBootMybaitsPlusMysql开发测试接口 1.2.1 添加依赖配置pom.xml 1.2.2 添加配置 application.properties 1.2.3 开发接口 ​ 2.分布式链路追踪的卧底 Skywalking Agent 探针介绍 2.1 Skyw…
阅读更多...
Java设计模式-解释器模式Interpreter

Java设计模式-解释器模式Interpreter

介绍 在编译原理中&#xff0c;一个算术表达式通过词法分析器形成词法单元&#xff0c;而后这些词法单元再通过语法分析器构建语法 分析树&#xff0c;最终形成一颗抽象的语法分析树。这里的词法分析器和语法分析器都可以看做是解释器解释器模式&#xff08;Interpreter Patte…
阅读更多...
Linux操作系统使用git提交代码

Linux操作系统使用git提交代码

引言&#xff1a; 北京时间 2023/1/27/9:50&#xff0c;今天的起床时间9:05&#xff0c;可以看出我们是提前了一些些&#xff0c;但是不是我的功劳&#xff0c;当然也不是我的闹钟的功劳&#xff0c;毕竟我的闹钟是8:20和8&#xff1a;50的&#xff0c;因为我亲爱的老妈……懂…
阅读更多...
threejs相机控件使用记录

threejs相机控件使用记录

文章目录前言控件列表轨迹球控制器&#xff08;TrackBallControls&#xff09;第一人称控制器&#xff08;FirstPersonControls&#xff09;飞行控制器&#xff08;FlyControls&#xff09;轨道控制器&#xff08;OrbitControls&#xff09;总结前言 threejs提供了很多摄像机控…
阅读更多...
mixamo和ue小白人映射关系以及让mixamo绑定的人物在场景中运动的多种方法实践...

mixamo和ue小白人映射关系以及让mixamo绑定的人物在场景中运动的多种方法实践...

ue中的root->Hips ue中 ik_foot_l ik_foot_r下面有foot_r 在mixamo下面leftfoot对应ik_foot_l 但是foot_l 只能给他对应leftToeBase 了 image.pngspline 盆骨对应pelvis 在绑定控制中进行修改即可. image.png方法一 拷贝动画蓝图 [本人原创方法] 此方法毕竟操蛋,虽然完美兼容…
阅读更多...
Linux驱动开发基础__休眠与唤醒

Linux驱动开发基础__休眠与唤醒

目录 1 适用场景 2 内核函数 2.1 休眠函数 2.2 唤醒函数 3 驱动框架 4 编程 4.1 gpio_key_drv.c 4.2 button_test.c 4.3 Makefile 1 适用场景 在前面引入中断时&#xff0c;我们曾经举过一个例子&#xff1a; 妈妈怎么知道卧室里小孩醒了&#xff1f; 休眠-唤醒&…
阅读更多...
pytorch深度学习案例（一）——手写数学符号识别

pytorch深度学习案例（一）——手写数学符号识别

文章目录前言简介数据集项目结构utils模块dataLoadermodelsplotShowtrain模块predict模块下载地址前言 在前面的两篇文章中我们介绍了现代计算机视觉中常见的结构化和非结构化的CNN模型&#xff0c;本篇我们将使用这些CNN模型在手写数学符号数据集上进行识别。 CNN模型的介绍请…
阅读更多...
2022回顾

2022回顾

2022年回顾 前言 新年和亲朋好友的相聚差不多接近尾声&#xff0c;假期也所剩无几&#xff0c;开始静下心来写作&#xff0c;回顾一下我的2022年&#xff0c;看下自己去年 做得好的和不足&#xff0c;展望下2023&#xff0c;开始新一年的生活。&#xff08;因为是公历2023年…
阅读更多...
Grafana 系列文章（一）：基于 Grafana 的全栈可观察性 Demo

Grafana 系列文章（一）：基于 Grafana 的全栈可观察性 Demo

&#x1f4da;️Reference: https://github.com/grafana/intro-to-mlt 这是关于 Grafana 中可观察性的三个支柱的一系列演讲的配套资源库。 它以一个自我封闭的 Docker 沙盒的形式出现&#xff0c;包括在本地机器上运行和实验所提供的服务所需的所有组件。 Grafana 全栈可观察…
阅读更多...
剑指 Offer 第9天 第10天

剑指 Offer 第9天 第10天

目录 剑指 Offer 42. 连续子数组的最大和 剑指 Offer 47. 礼物的最大价值 剑指 Offer 46. 把数字翻译成字符串 剑指 Offer 48. 最长不含重复字符的子字符串 剑指 Offer 42. 连续子数组的最大和 输入一个整型数组&#xff0c;数组中的一个或连续多个整数组成一个子数组。求所…
阅读更多...
Python self用法详解

Python self用法详解

在定义类的过程中&#xff0c;无论是显式创建类的构造方法&#xff0c;还是向类中添加实例方法&#xff0c;都要求将 self 参数作为方法的第一个参数。例如&#xff0c;定义一个 Person 类&#xff1a;class Person: def__init__(self): print("正在执行构造方法") #…
阅读更多...
大数据项目---电商数仓（三）

大数据项目---电商数仓（三）

目录 1.即席查询_Presto概述 2.即席查询_Presto_Server的部署 3.即席查询_Presto_Server启动 4.即席查询_命令行客户端说明 5.即席查询_LZO说明 6.即席查询_Presto_web端口 ​编辑 7.即席查询_Presto使用注意事项/优化 8.即席查询_Kylin简介 9.即席查询_前置概念 10.即…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023