在 PID控制中，微分信号的引入可改善系统的动态特性，但也易引进高频干扰，在误差扰动突变时尤其显出微分项的不足。若在控制算法中加入低通滤波器，则可使系统性能得到改善。

克服上述缺点的方法之一是在 PID算法中加入一个一阶惯性环节（低通滤波器)，可使系统性能得到改善。

不完全微分PID的结构如图(a)、(b）所示，其中图（a）是将低通滤波器直接加在微分环节上，图（b）是将低通滤波加在整个PID控制器之后。下面以图（a）为例进行仿真说明不完全微分PID如何改进了普通PID的性能。

仿真实例：

采用第一种不完全微分算法，被控对象为一时滞系统传递函数：

在对象的输出端加幅值为0.01的随机信号n(k)。采样时间为20ms.低通滤波器为：

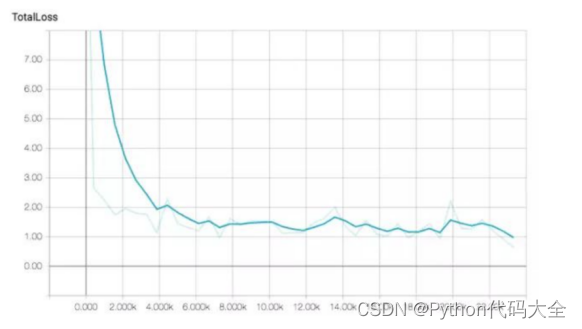
取M=1，采用具有不完全微分PID方法，其控制阶跃响应结果如图1所示。取M=2，采用普通PID 方法，阶跃响应结果如图2所示。由仿真结果可以看出，引入不完全微分后，能有效地克服普通PID的不足。尽管不完全微分PID控制算法比普通PID控制算法要复杂些，但由于其良好的控制特性，近年来越来越得到广泛的应用。

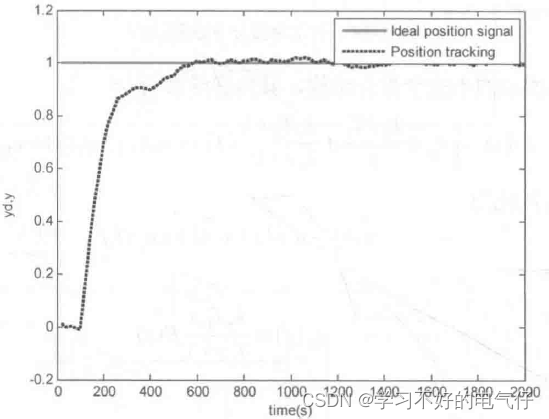
图1 不完全微分控制阶跃响应（M=1）

图2 普通PID控制阶跃响应（M=2）

仿真程序：

%PID Controler with Partial differential

clear all;

close all;

ts=20;

sys=tf([1].[60,1].'inputdelay',80);

dsys=c2d(sys,ts,'zoh');

[num,den]=tfdata(dsys,'V);

u_1=0;u_2=0;u_3=0;u_4=0;u_5=0;

ud_1=0;

y_1=0;y_2=0;y_3=0;error_l=0;

ei=0;

for k=1:1:100

time(k)=k*ts;

yd(k)=1.0;

%Linear model

y(k)=-den(2)*y_l+num(2)*u_5;

n(k)=0.01*rands(1);

y(k)=y(k)+ n(k);

error(k)=yd(k)-y(k);

%PID Controller with partly differential

ei=ei+errorKy

kc=0.30;

ki=0.0055;TD=140;

kd=kc*TD/ts;

Tf=180;

Q-tf[1],[Tf,1]); %Low Freq Signal Filter

M=2;

if M==1 %Using PID with Partial differential

alfa=Tf(ts+Tf);

ud(k)=kd*(1-alfa)*(error(k)-error_1)Halfaud_l;

u(k)=ke*error(k)+ud(k)+ki*ei;

ud_1=ud(k);

elseif M==2 %Using Simple PID

u(k)=kc*error(k)+kd*(error(k)-error_1)+ki*ci;

end

%Restricting the output of controller

if u(k)>=10

u(k)=10;

end

if u(k)<=-10

u(k)=-10;

end

u_5=u_4;u_4=u_3;u_3=u_2;u_2=u_1;u_1=u(k);

y 3=y 2:y_2=y_1;y_1=y(k);

error_l=error(k);

end

figure(1);

plot(time,yd,'r,time,y,'k:',linewidth',2);xlabel('time(s)');ylabel('yd.y');

legend('Ideal position signal', Position tracking);figure(2);

plot(time,u,'r.'linewidth' 2);xlabel('time(s));ylabel('u');figure(3);

bode(Q,T);dcgain(Q);