分治法简介
分治法思想
分治法,就是将一个难以解决的大问题给分成多个规模较小的子问题,分别解决各个子问题,最后合并子问题的解得到原问题的解。
分治法求解过程:
1、划分(分):
把规模为n的原问题划分为k(通常k=2)个规模较小的子问题,再对子问题继续划分,直到到达最小子问题时终止(比如说元素只剩1个),一般使用递归来实现。
3、合并(治):
从已知解的最小子问题开始,从底至顶地将子问题的解进行合并,从而构建出原问题的解。合并的代价因情况不同有比较大的差异,分治算法的效率很大程度上依赖合并的实现。
分治思想在生活中的应用
1、做饭
在做饭的过程中,需要准备主食、汤、菜。
将整个做饭分解成蒸米饭、煮汤、烧菜三部分,三部分完成后再整合再一起放在桌子上,完成做饭。
2、人口普查
全国人口普查,将问题拆分成省级,市级,区级,乡镇级,街道级,小区级。
然后依次向上汇报进行汇总,然后自下而上统计人数。
如何判断是否为分治问题:
一个问题是否适合使用分治解决,通常可以参考以下几个判断依据。
- 问题可以分解:原问题可以分解成规模更小、类似的子问题,以及能够以相同方式递归地进行划分。
- 子问题是独立的:子问题之间没有重叠,互不依赖,可以独立解决。
- 子问题的解可以合并:原问题的解通过合并子问题的解得来。
经典案例-归并排序
分析:
对于一个无序数组,对其进行排序,其满足分治的三个要求:
- 问题可以分解:递归地将数组(原问题)划分为两个子数组(子问题)。
- 子问题是独立的:每个子数组都可以独立地进行排序(子问题可以独立进行求解)。
- 子问题的解可以合并:两个有序子数组(子问题的解)可以合并为一个有序数组(原问题的解)。
过程图解:
使用递归不断的对原数组进行划分,直到划分为最小子问题(单个元素,单个元素一定是有序的)。
然后再依次合并子数组,将其合并为一个较大的有序数组。

前面说过,分治算法的效率很大程度上依赖合并的实现,这里合并如何实现是比较重要的。
合并数组操作:
两个子数组从下标0开始,依次比较,拿出其中较小的放入合并后数组中。
最后将剩余子数组的数据依次放入结果数组中。
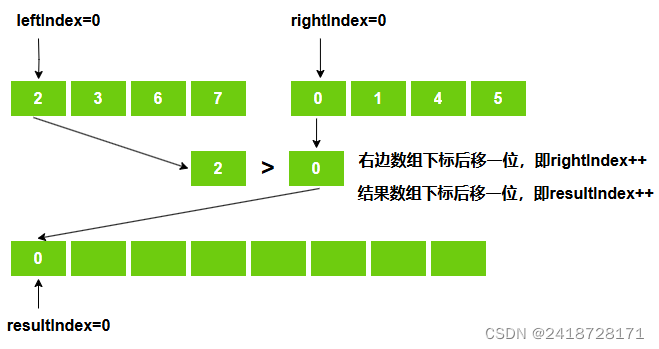
以上面 {2、3、6、7} 与 {0、1、4、5} 两个有序子数组合并为例:
1、初始化
左边数组、右边数组、合并后数组都从下标0开始,即 leftIndex = rightIndex = resulrIndex = 0
2、第一趟比较
右边数组下标rightIndex=0的位置值小于左边数组下标leftIndex=0位置的值。
先将右边数组下标rightIndex=0的位置值放入结果数组中,然后右边数组下标向后移动一位,结果数组下标向后移动,左边数组下标不动。
即result[resultIndex++] = right[RightIndex++]。
3、第二趟比较
右边数组下标rightIndex=1的位置值小于左边数组下标leftIndex=0位置的值。
先将右边数组下标rightIndex=1的位置值放入结果数组中,然后右边数组下标向后移动一位,结果数组下标向后移动,左边数组下标不动。
即result[resultIndex++] = right[RightIndex++]。
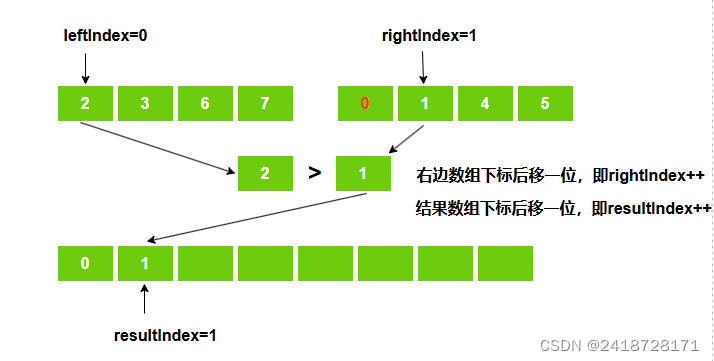
4、第三趟比较

5、第四躺比较

6、第五躺比较

7、第六躺比较

8、第7躺比较
此时,右边数组遍历结束,左边数组还有剩余。
此时依次将左边数组中数据放入结果数组。

9、最后

代码实现:
/**
* @param data 待排序数组
* @param left 待排序数组起始下标
* @param right 待排序数组终止下标
* @return
*/
public static int[] execute(int[] data, int left, int right) {
// 达到最小子问题,即只有一个元素,那么这个元素一定是有序的
if (left == right) {
return new int[]{data[left]};
}
/**
* 定义临时变量
* midIndex:数组中间值,即将数组划分为 left -> midIndex 和 midIndex+1 -> right 两部分
* leftIndex:合并两个有序子数组时,记录 left -> midIndex 数组的下标
* rightIndex:合并两个有序子数组时,记录 midIndex+1 -> right 数组的下标
* resultIndex:合并两个有序子数组时,记录 合并后有序数组 的下标
*/
int midIndex = (right - left) / 2 + left,
leftIndex = 0, rightIndex = 0, resultIndex = 0;
// 递归求解 left -> midIndex 部分,使这部分有序
int[] leftResult = execute(data, left, midIndex);
// 递归求解 midIndex+1 -> right 部分,使这部分有序
int[] rightResult = execute(data, midIndex + 1, right);
// 存储合并后的有序数组
int[] result = new int[right - left + 1];
// 合并
while (leftIndex < leftResult.length && rightIndex < rightResult.length) {
result[resultIndex++] =
leftResult[leftIndex] <= rightResult[rightIndex] ?
leftResult[leftIndex++] : rightResult[rightIndex++];
}
// left -> midIndex 部分有剩余,依次填入合并后有序数组
while (leftIndex < leftResult.length) {
result[resultIndex++] = leftResult[leftIndex++];
}
// midIndex+1 -> right 部分有剩余,依次填入合并后有序数组
while (rightIndex < rightResult.length) {
result[resultIndex++] = rightResult[rightIndex++];
}
return result;
}