104.二叉树的最大深度

代码随想录文档讲解
LeetCode
斜体样式
本题在前一章节层序遍历时已完成。（迭代法：层序遍历）
（↓递归法：后序遍历）
首先明确二叉树的深度和高度：
深度为到根节点的距离，如节点20，深度为2；节点6，深度为3（从1开始算深度）
高度为到叶子节点的距离，如节点7，高度为1，节点20，高度为2，节点3，高度3

  	3
   /   \
  9		20
  		/	\
  	  15	 7

如何遍历呢？
高度：后序遍历（左右根），从下往上计数
深度：前序遍历（根左右），从上往下计数

二叉树的最大深度：根节点的高度

伪代码c++：

int getheight(node){
	if(node==NULL) return 0;
	int leftheight = getheight(node->left);
	int rightheight = getheight(node->right);
	int height = 1+max(leftheight, rightheight);
	return height;
// 上述if后面的代码可以合并为一行
// return 1+max(getheight(node->left), getheight(node->right));
}

python代码：

# 方法一
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
from collections import deque
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root: return 0
        leftheight = self.maxDepth(root.left)
        rightheight = self.maxDepth(root.right)
        return 1 + max(leftheight, rightheight)

# 方法二：之前的实现—层序遍历
from collections import deque
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        result = 0
        queue = deque([root])
        while queue:
            size = len(queue)
            result += 1
            while size:
                size -= 1
                cur = queue.popleft()
                if cur.left:
                    queue.append(cur.left)
                if cur.right:
                    queue.append(cur.right)
        return result

111.二叉树的最小深度

leetcode题目链接
代码随想录文档讲解

最小深度：根节点到最近叶子节点的深度

思路：

遍历顺序三种都可以：

1. 前序遍历求深度（根左右）
2. 迭代法，层序遍历
3. 但后序遍历代码更简洁，伪代码使用后序遍历

后序遍历：将孩子节点的情况返回给根节点，根节点记录

本题可能存在的陷阱（见代码）

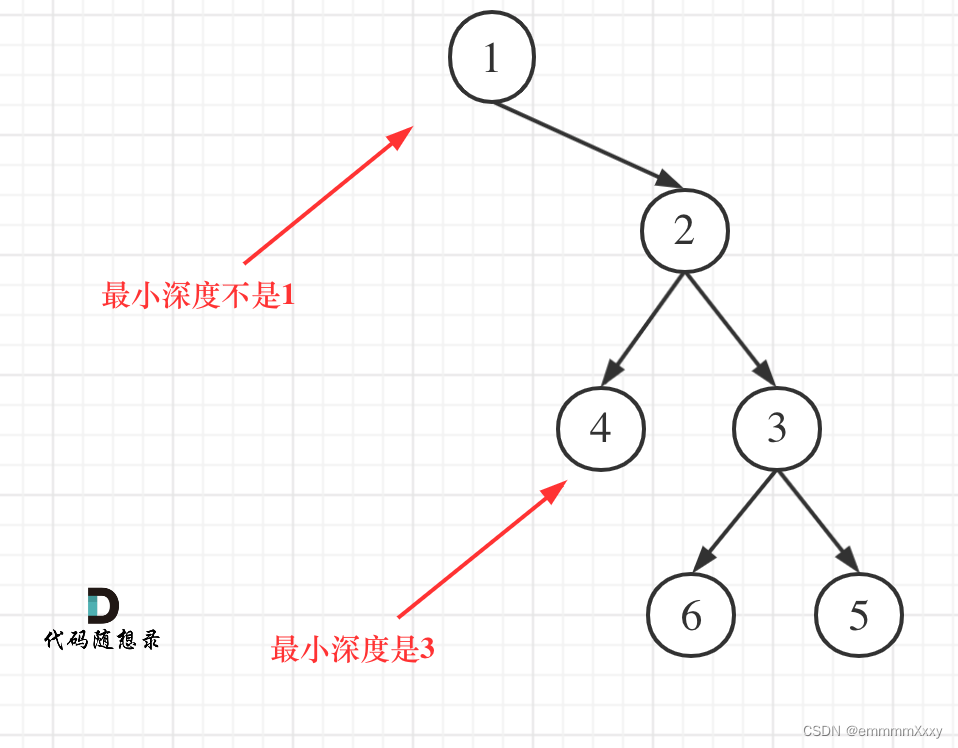
伪代码（C++）：

int getheight(node){
	if(node==NULL) return 0;
	int leftheight = getheight(node->left);
	int rightheight = getheight(node->right);
	// 有陷阱 如果节点左子树为空，但右子树不为空，会出现错误情况
	if(node->left == NULL && node->right != NULL){
		return 1 + rightheight;
	}
	if(node->left != NULL && node->right == NULL){
		return 1 + leftheight;
	}
	int result = 1 + min(leftheight, rightheight);
	return result;
}

python代码：

# 后序遍历
from collections import deque
class Solution:
    def minDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        leftheight = self.minDepth(root.left)
        rightheight = self.minDepth(root.right)

        if root.left and not root.right:
            return 1 + leftheight
        if not root.left and root.right:
            return 1 + rightheight
        result = 1 + min(leftheight, rightheight)
        return result
        
# 层序遍历
from collections import deque
class Solution:
    def minDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        res = 1
        q = deque([root])
        while q:
            size = len(q)
            while size:
                cur = q.popleft()
                if cur.left:
                    q.append(cur.left)
                if cur.right:
                    q.append(cur.right)
                if not cur.left and not cur.right:
                    return res
                size -= 1
            res += 1

222.完全二叉树的节点个数

leetcode题目链接
代码随想录文档讲解

思路：

如果当成普通二叉树，前中后序都可以求得二叉树的节点个数，层序遍历的迭代法也可以。

伪代码（C++）：

int getNum(node){
	if(node==NULL) return 0;
	leftnum = getNum(node->left);        //左
	rightnum =  getNum(node->right);  //右
	result = 1 + leftnum + rightnum;      //中
}

若使用完全二叉树的特性：
除了底层节点，上面的节点都是满的，底层节点从左到右是满的。
满二叉树节点数量的计算公式：$2^n-1$

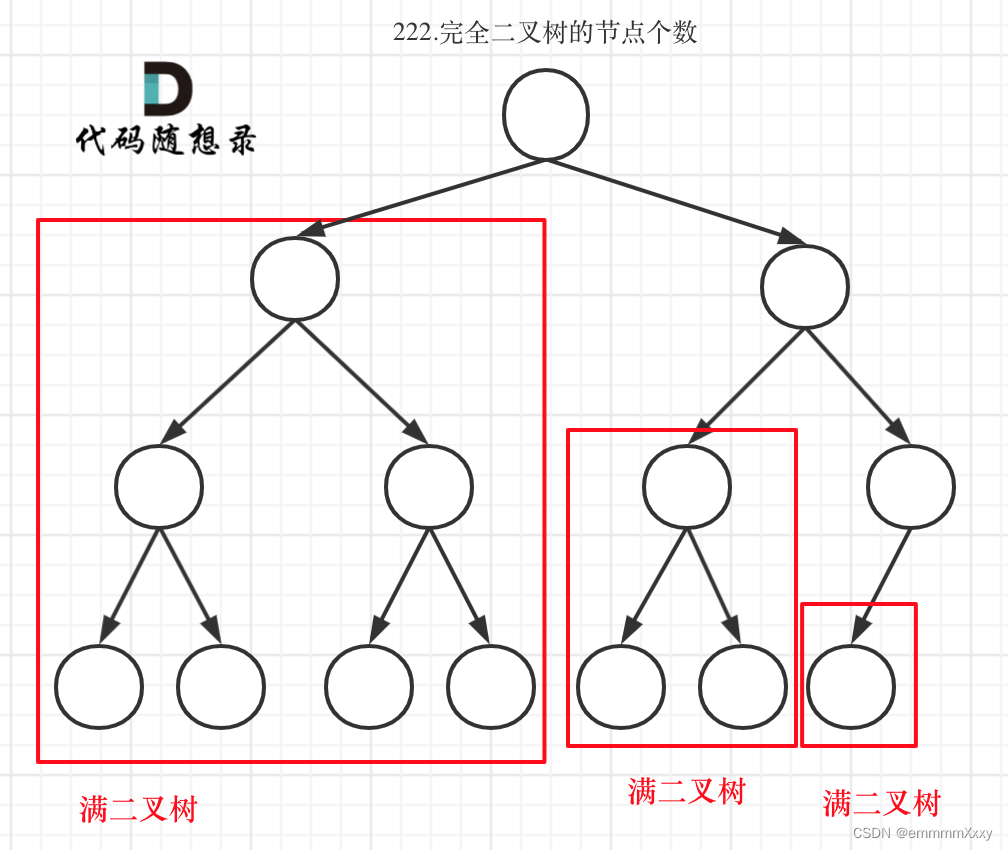
如何去判断子树是满二叉树呢？
如果是满二叉树的话 ，向左遍历的深度和向右遍历的深度是相等的。
如果不是满二叉树，继续向下遍历，子树可能是满二叉树。

子树如果为满二叉树可以根据公式计算节点数量，然后返回给根节点。

伪代码（C++）：

本题的终止条件：

1. 节点为空
2. 子树为满二叉树

int getNum(node){
	if(node == NULL) return 0;
	left = node->left;
	right = node->right;
	leftdeepth = 0;
	rightdepth = 0;
	while(left)[
		left = left->left;
		leftdepth++;
	}
	while(right){
		right = right->right;
		rightdepth++;
	}
	if(leftdepth == rightdeepth) return 2<<leftdepth - 1; // 位运算 
	// 2 左移一位： 2<<1，相当于2的2次方:4

	leftnum = getNum(node->left);
	rightnum =  getNum(node->right);
	result = 1 + leftnum + rightnum;
	return result;
}

python代码：

# 普通二叉树
class Solution:
    def countNodes(self, root: Optional[TreeNode]) -> int:
        if not root: return 0
        return 1 + self.countNodes(root.left) + self.countNodes(root.right)
  
# 完全二叉树
class Solution:
    def countNodes(self, root: Optional[TreeNode]) -> int:
        if not root: return 0
        leftdepth = 0
        rightdepth = 0
        left = root.left
        right = root.right
        while left:
            leftdepth += 1
            left = left.left
        while right:
            rightdepth += 1
            right = right.right
        if leftdepth == rightdepth:
            return (2<<leftdepth) - 1
            # return 2 ** (leftdepth+1) - 1
        return 1 + self.countNodes(root.left) + self.countNodes(root.right)