探地雷达正演模拟，基于时域有限差分方法，三

回顾上一章内容，主要讲了FDTD及基于C++的实现方式和边界条件处理，这一章主要内容有两点：1、基于实际操作流程的GPR正演模拟（宽角法和剖面法）；2、简单并行化加速GPR正演模拟（基于OpenMP）。

根据参考文献在GPR勘探中，探测方式主要有两种，一种是宽角法，类似于地震勘探的共炮集记录，另一种是剖面法，但是宽角法在实际工区勘探中由于经费限制，无法大量布置接收天线在阵列，因此，实际工区内的主要勘探方式是剖面法，该方法中接收天线和发射天线以固定间距沿测线以固定步长移动，并将各道接收记录结合形成雷达剖面，本章以三层模型为例进行讲解。

首先是宽角法，只需要在第二章FDTD函数中创建文件流，并输出测线接收记录即可：

// editor：WangBoHua
// date：2024.6.12
//创建文件流
fstream ofs;
//建立输出文件地址
string filename="file_path";
//打开文件
ofs.open(filename,ios::out);
for(int n=0;n<simulation_Step;n++){
    //Sample是采样率
    if(n%Sample==0){
        for(int i=0;i<cellNumForY;i++){
            ofs<<Ey[CpmlBound+1][i]<<'\t';
        }
        ofs<<endl;
    }

}
ofs.close()

设计采样率为1*courant，这里给出Python绘图代码：

#editor：WangBoHua
#date：2024.6.12
# for gpr grawing
import numpy as np
import matplotlib.pyplot as plt
# 宽角法雷达记录
t=np.linspace(0,6000,7001,dtype=float)*courant*1e9
x=np.linspace(0,5,1000,dtype=float)
rec=np.genfromtxt("接受记录位置")
fig2=plt.figure(dpi=1000)
ax7=fig2.add_subplot(1, 1, 1)
ax7.pcolormesh(rec, vmin=-0.001,vmax=0.002, cmap='jet', rasterized=True)
ax7.tick_params(direction='in', width=0.5)
ax7.invert_yaxis()
ax7.set_xlabel("x/m")
ax7.set_ylabel("t/ns")
ax7.set_title("Wide")
ax7.xaxis.set_ticks_position('top') 
# np.savetxt("C:/Users/12981/Desktop/signal25.data",rec)
# plt.rcParams['savefig.dpi'] = 800  # 图片像素
# plt.savefig("A-Scan.png",
#             bbox_inches='tight')  # 直接保存成png格式图片就好
# plt.savefig("A-Scan.pdf",
#             bbox_inches='tight')  # 修图的话改成pdf格式保存

宽角度法的计算结果：

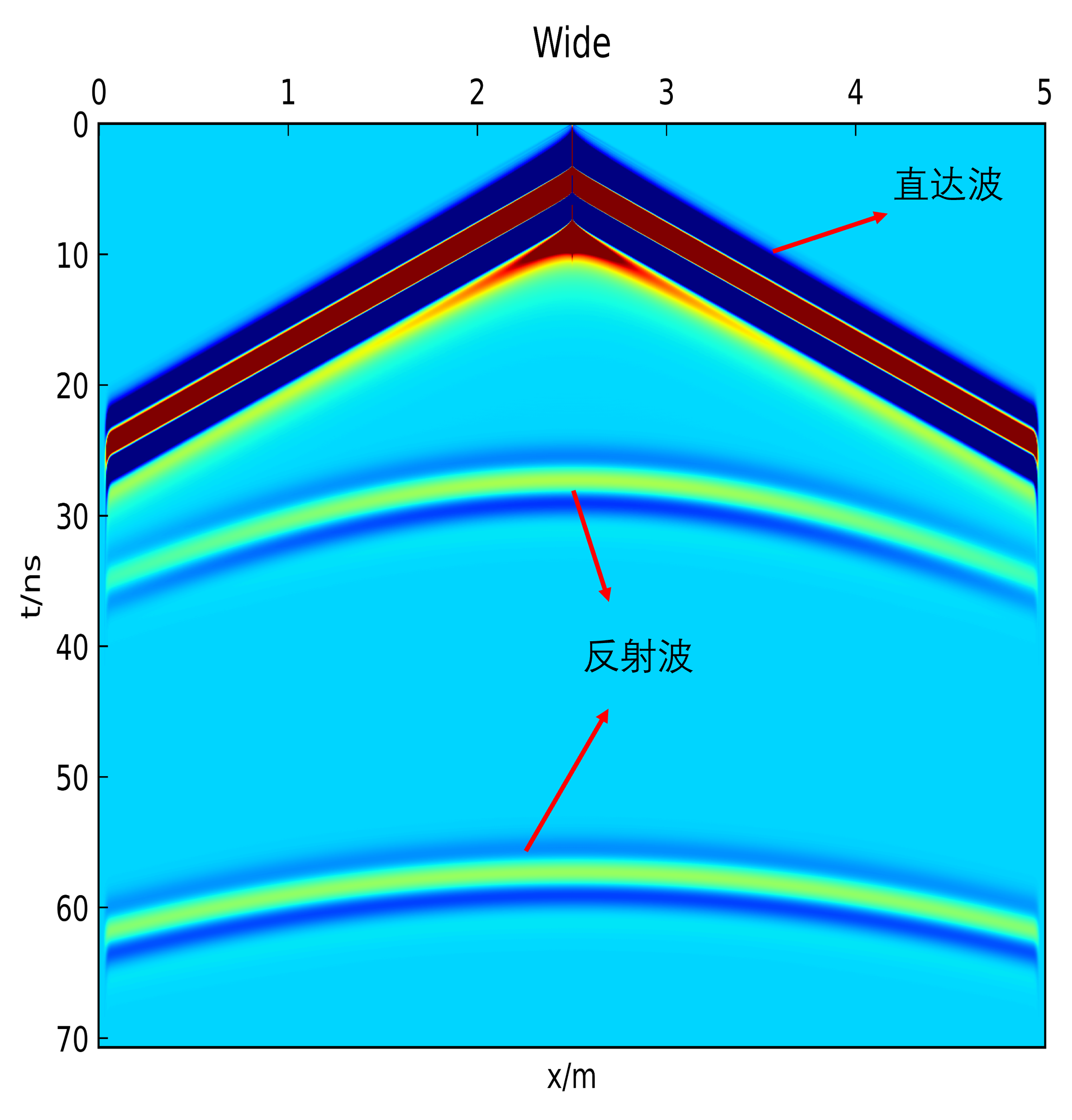
但就和上文中说的那样，实际工作中不可能构成天线阵列，宽角法只能是模拟后用作参考。

是剖面法的计算成本较大，但较宽角法而言，剖面图像能够更加直观的反映地下结构和情况，实际实现方式也非常经济，所以在实际勘探工作中使用较多。这里由于时间原因，只展示代码和三层模型的剖面记录。

// editor：WangBoHua
// date：2024.6.12
//创建一个Main函数
int main(){
    for (int j = CpmlBound + 1; j < cellNumForY - CpmlBound - 1; j += 5) {
        int tracenum=0;
		if (j + 8 < cellNumForY - CpmlBound - 1) {
			cout << j + 8 << "trace" << endl;
			tracenum++;
			FDTD(j, j + 8,  SimulationSteps);//一次记录一个道集
		}
	}

}
//在FDTD函数中创建一个vector数组
    vector<double>receiver(Simulation_steps,0.0);
    //FDTD的FOR循环迭代中进行记录
        receiver[i]=Ey[cpmlBound+1][receive];
    //FDTD循环后创建文件流并输出
	char filename[200];
	sprintf_s(filename, "%s%d%s", "path", receivery, ".data");
	fstream ofs;
	ofs.open(filename, ios::out);
	ofs.clear();
    for(int i=0;i<simulation_Steps;i++){
    ofs<<receiver[i]<<endl;
    }
    ofs.close()

时间原因，这里仅展示一幅三层剖面记录：

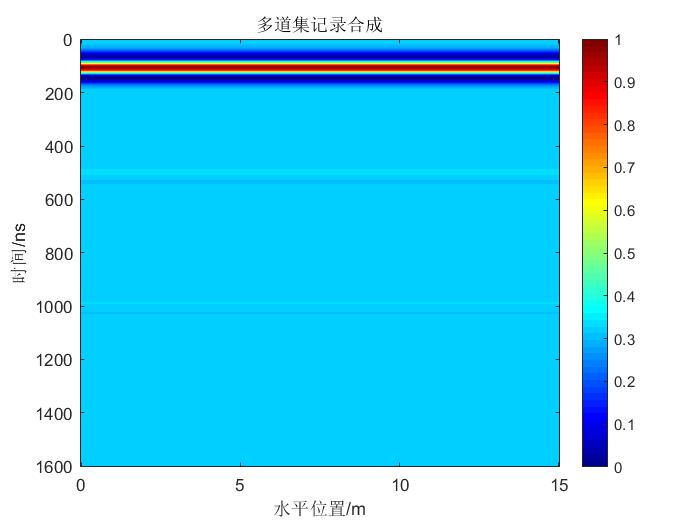
这幅图的时间做的有点不对，但是仅是用来参考就行。

剖面记录合成代码，使用Python：

#editor： WangBoHua
#date：2024.6.12
# 剖面法雷达记录
import cv2
import numpy as np
from math import ceil
import matplotlib.pyplot as plt
Single = np.genfromtxt("某一道记录的位置")
# 合成时的路就修改
Path = "道集记录的位置"
tail = ".data"
Pathall = []
dt = 1.92e-11#就是Courant
Cpml = 20
Cell = 1000
i = Cpml+1
#中心是这一段，但是要根据自己代码的实际情况调试
while i+8 < Cell-Cpml-1:
    Pathall.append(Path+str(i+8)+tail)
    i = i+2
data = np.zeros([len(Single), len(Pathall)]).reshape(len(Single), len(Pathall))
for i in range(len(Pathall)):
    data[:, i] = np.genfromtxt(Pathall[i])
Gaussian = cv2.GaussianBlur(data, ksize=(
    ceil(2*3)+1, ceil(2*3)+1), sigmaX=0.5, sigmaY=0.5)#做不做高斯滤波都行，做完之后图像能平滑些
t = np.linspace(0, len(Single), len(Single), dtype='float')*dt*1e9
x = np.linspace(0, 30, len(Pathall), dtype='float')
x1=np.linspace(0, 30, 1000, dtype='float')
plt.figure(figsize=(16, 9))
plt.pcolormesh(x, t, data, vmin=-20, vmax=20,
               cmap='jet', rasterized=True)
plt.gca().invert_yaxis()
plt.gca().tick_params(direction='in', width=0.5)
plt.gca().xaxis.set_ticks_position('top') 
plt.xlabel("location")
plt.ylabel("time")
plt.show()

上述已经解决了宽角法和剖面法记录的计算和合成，下面看一个很有意思的问题：并行化计算以提高代码运行速度（In OpenMP）：

当前并行化方式主要有三种：1、OpenMP技术、2、MPI技术、3、CUDA编程。OpenMP和CUDA是较容易理解的并行计算方式，前者是榨干CPU的性能和运算效率，后者是使用显卡（最好是Nvidia的，其他公司的没接触过，也不太了解是否和英伟达CUDA逻辑相同，GPRMax已经实现了这种技术）进行计算，MPI技术个人认为如果能够连接多台电脑的话，也是可以试一试，但考虑到实验室代码不允许外传以及GPR正演的使用对象对并行编程要求并不是太高的情况，这里仅提供OpenMP加速的计算方式，其余两种可以根据参考文献5中的配套代码学习。

OpenMP是一种非常简单的并行编程技术，可以简单的介绍一下：假如说，我们使用的计算机CPU有12个核心，那我们在OpenMP中就可以开启2倍的线程数量（但一般得空出来几个，不然电脑的其他后台程序会很卡），每个线程都可以单独计算，通过这种方式就能够有效缩短计算时间，提高计算效率。

Visual Studio已经集成了这种技术，在解决方案的属性中就可以打开：

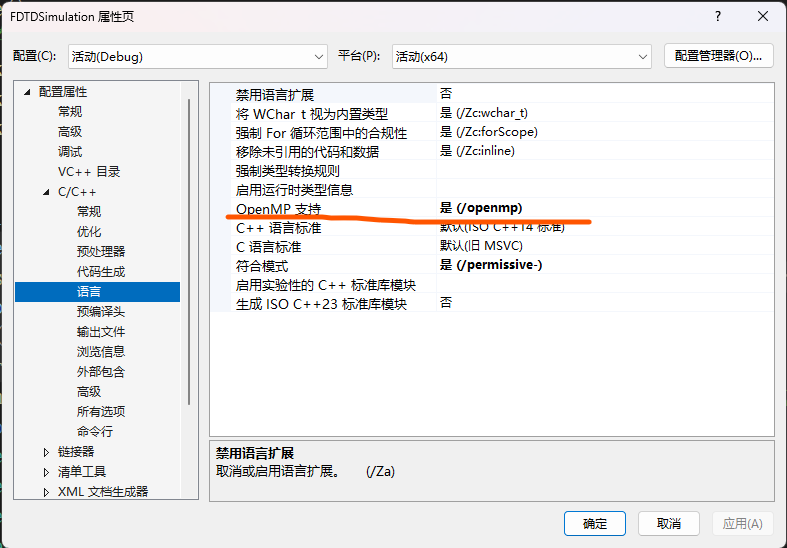
应用并确定就好。

基本实现代码也不需要对第二章的代码进行修改，只需要添加语句如下：

#include<omp.h>
//main函数中
//设置线程数量
omp_set_num_threads(10)

#pragma omp parallel  for ordered schedule(guided) //代码并行语句，这里的guided是启发式内存分配：
	for (int i = 0; i < cellNumForX + 1; i++) {}

值得注意的是，双重for循环中只能在外侧for循环上方添加，内层添加后计算数据会出错，而且有两个地方不可以使用，一是第二章中的CPML函数计算，不要添加OpenMP并行语句，另一个是FDTD中的时间循环，也是无法添加的。

简单理解就是，我们使用OpenMP把for循环分布在不同核心上进行计算，这样就可以大幅提高计算效率了，可以做实际运算进行比较：以2000步为例，使用OpenMP:

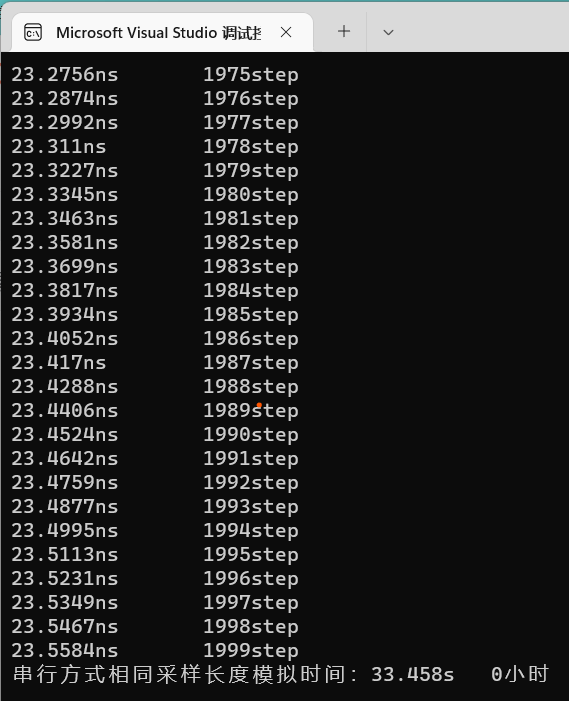
使用OpenMP用时约33.5s，

不适用OpenMP时：

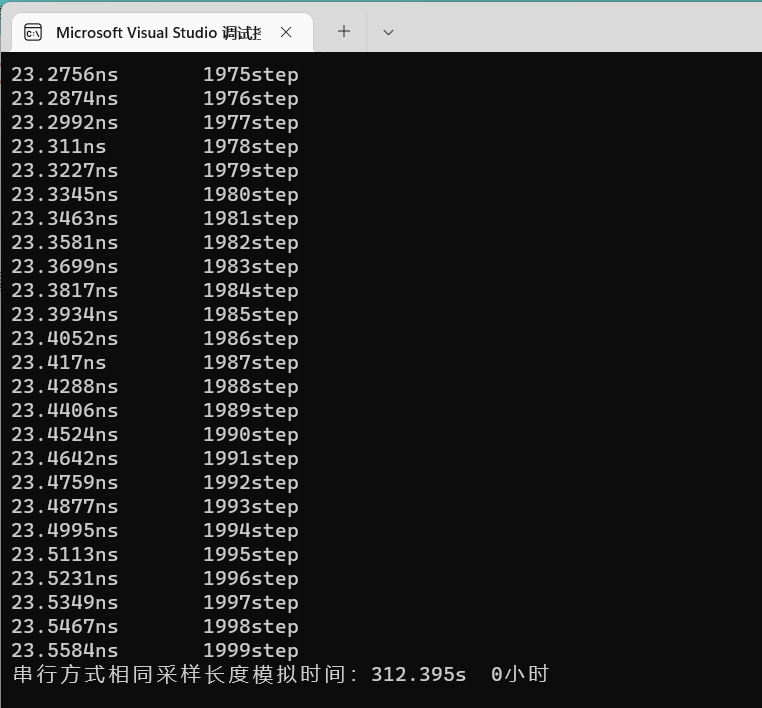
加速比A约为9.34，使用OpenMP技术能够在一定程度上加速FDTD的计算，进一步帮助我们快速获得雷达接收信号以合成正演剖面。

声明：欢迎上述代码和图片引用，但请标注公式和图片来源,创作不易，请多多支持，非常感谢！

参考文献：葛德彪,闫玉波. 电磁波时域有限差分法第2版．西安:西安电子科技大学出版社,2005：133-137,37,118．

Shen, H, Y., Li, X, S., Duan, R, F., et al., (2023), Quality evaluation of ground improvement by deep cement mixing piles via ground-penetrating radar. Nature Communications,14,34-48. https://doi.org/10.1038/s41467-023-39236-4

冯德山,戴前伟,何继善等. 探地雷达GPR正演的时域有限差分实现(英文)[J].地球物理学进展,2006,(02):630-636.

冯德山。探地雷达数值模拟及程序实现。

何兵寿，宋鹏，刘颖等.并行编程原理与程序设计

李静,刘津杰,曾昭发等. 基于变换光学有限差分探地雷达数值模拟研究[J].地球物理学报,2016,59(06):2280-2289.