监督学习线性回归、逻辑回归、决策树、支持向量机、K近邻、朴素贝叶斯算法精讲，模型评估精讲

关注作者，复旦AI博士，分享AI领域与云服务领域全维度开发技术。拥有10+年互联网服务架构、AI产品研发经验、团队管理经验，同济本复旦硕博，复旦机器人智能实验室成员，国家级大学生赛事评审专家，发表多篇SCI核心期刊学术论文，阿里云认证的资深架构师，项目管理专业人士，上亿营收AI产品研发负责人。

1. 介绍

1.1 什么是监督学习

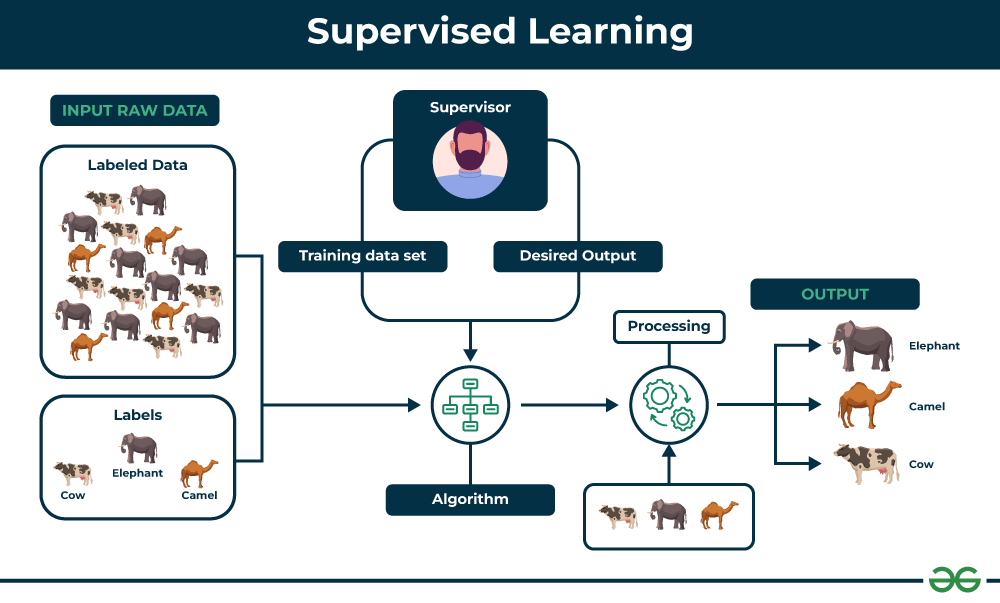
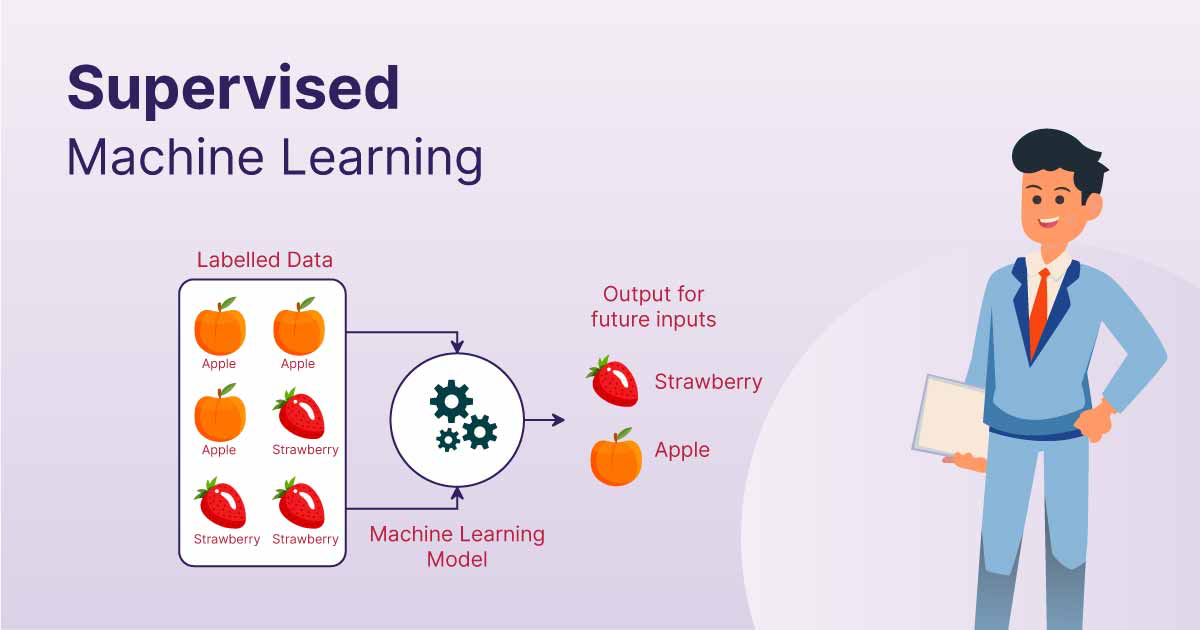
监督学习（Supervised Learning）是机器学习的一个重要分支，其核心目标是通过已知的训练数据（包括输入和对应的输出）来学习一个映射函数，使其能够对未知的数据进行有效的预测。在监督学习的过程中，算法通过观察大量的示例数据，逐步调整其内部参数，使得预测结果尽可能接近真实值。

具体而言，监督学习的任务可以分为两类：

• 回归（Regression）：预测连续数值。例如，根据历史房价数据预测未来房价。
• 分类（Classification）：预测离散标签。例如，根据邮件内容预测其是否为垃圾邮件。

在监督学习中，训练数据通常以特征-标签对（Feature-Label Pair）的形式存在。特征是用来描述数据点的属性，标签是我们希望预测的目标变量。例如，在垃圾邮件分类问题中，特征可以是邮件的词频，标签则是“垃圾邮件”或“非垃圾邮件”。

监督学习的基本流程

1. 数据收集：收集大量的已标注数据。标注数据包括输入特征和对应的输出标签。
2. 数据预处理：对数据进行清洗、处理和转换，以便于模型处理。包括处理缺失值、特征选择和特征工程等。
3. 模型选择：选择适合的算法，如线性回归、逻辑回归、决策树等。
4. 模型训练：使用训练数据来训练模型。模型通过不断调整其参数，使得预测结果尽可能接近真实标签。
5. 模型评估：使用独立的验证数据集评估模型性能。常见的评估指标有准确率、精确率、召回率等。
6. 模型优化：根据评估结果对模型进行调整和优化。
7. 模型部署：将训练好的模型应用到实际场景中进行预测。

1.2 监督学习与其他学习方法的比较

为了更好地理解监督学习，有必要将其与其他常见的机器学习方法进行比较，主要包括无监督学习和强化学习。

无监督学习（Unsupervised Learning）

无监督学习与监督学习的主要区别在于训练数据没有标签。在无监督学习中，算法需要自行发现数据的内在结构和模式。常见的无监督学习任务包括聚类（Clustering）和降维（Dimensionality Reduction）。例如，K-means算法用于将数据点聚类到不同的组中，而PCA（Principal Component Analysis）用于减少数据的维度。

强化学习（Reinforcement Learning）

强化学习与监督学习的区别在于它关注的是如何在动态环境中通过试错来获得最大化的累积奖励。强化学习算法通过与环境不断交互，根据反馈奖励调整策略，以实现长期目标。例如，AlphaGo通过不断与自己对弈来提高棋艺，最终战胜了人类顶尖棋手。

1.3 监督学习的应用场景

监督学习在众多领域有广泛应用，以下是几个典型的应用场景：

• 自然语言处理（NLP）：文本分类、情感分析、机器翻译等。
• 计算机视觉：图像分类、人脸识别、目标检测等。
• 金融科技：信用评分、股票价格预测、欺诈检测等。
• 医疗健康：疾病预测、医学图像分析、基因组学数据分析等。
• 推荐系统：根据用户历史行为推荐商品、电影、音乐等。

1.4 监督学习的挑战

尽管监督学习在许多应用中表现出色，但它也面临一些挑战：

• 数据标注成本高：获取大量高质量的标注数据通常需要耗费大量的人力和时间。
• 模型泛化能力：训练模型如何在未见过的数据上表现良好，即避免过拟合。
• 数据偏差和公平性：训练数据中的偏差可能导致模型在实际应用中表现不公平。
• 计算资源需求：复杂模型的训练和预测过程需要大量的计算资源和时间。

2. 算法精讲

2.1 线性回归

线性回归（Linear Regression）是一种用于回归任务的基本且广泛应用的监督学习算法。它通过找到一条最佳拟合直线来预测目标变量（标签）的值。线性回归模型假设目标变量与输入特征之间存在线性关系，即目标变量可以表示为输入特征的线性组合。

2.1.1 线性回归简介

线性回归模型的形式可以表示为：

线性回归的目标是通过最小化误差项来找到最佳的系数和截距项，从而使模型对训练数据的预测尽可能准确。

2.1.2 线性回归的假设

在应用线性回归时，需要满足以下几个基本假设：

1. 线性关系：目标变量与输入特征之间存在线性关系。
2. 独立性：误差项彼此独立。
3. 同方差性：误差项的方差恒定（即误差的分布不随输入特征的变化而变化）。
4. 正态分布：误差项服从正态分布。

2.1.3 最小二乘法

线性回归中常用的参数估计方法是最小二乘法（Ordinary Least Squares, OLS），其目标是最小化残差平方和（Residual Sum of Squares, RSS）：

2.1.4 代码实现

下面是使用Python和PyTorch实现线性回归的示例代码：

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt

# 生成样本数据
np.random.seed(0)
X = np.random.rand(100, 1)
y = 5 + 3 * X + np.random.randn(100, 1)

# 将数据转换为PyTorch张量
X_tensor = torch.tensor(X, dtype=torch.float32)
y_tensor = torch.tensor(y, dtype=torch.float32)

# 定义线性回归模型
class LinearRegressionModel(nn.Module):
    def __init__(self):
        super(LinearRegressionModel, self).__init__()
        self.linear = nn.Linear(1, 1)
    
    def forward(self, x):
        return self.linear(x)

# 创建模型实例
model = LinearRegressionModel()

# 定义损失函数和优化器
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)

# 训练模型
num_epochs = 1000
for epoch in range(num_epochs):
    model.train()
    optimizer.zero_grad()
    outputs = model(X_tensor)
    loss = criterion(outputs, y_tensor)
    loss.backward()
    optimizer.step()
    
    if (epoch+1) % 100 == 0:
        print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')

# 打印模型参数
print(f'Intercept (b0): {model.linear.bias.item():.4f}')
print(f'Coefficient (b1): {model.linear.weight.item():.4f}')

# 可视化结果
model.eval()
predicted = model(X_tensor).detach().numpy()
plt.plot(X, y, 'ro', label='Original data')
plt.plot(X, predicted, label='Fitted line')
plt.legend()
plt.show()

代码解释：

1. 数据生成：使用随机数生成器生成输入特征 ( X ) 和目标变量 ( y )。
2. 数据转换：将numpy数组转换为PyTorch张量，以便进行模型训练。
3. 模型定义：定义一个简单的线性回归模型，包含一个线性层。
4. 模型实例化：创建模型实例。
5. 损失函数和优化器：使用均方误差（MSE）作为损失函数，随机梯度下降（SGD）作为优化器。
6. 模型训练：进行1000次迭代，每次迭代中计算预测值、损失，反向传播并更新模型参数。
7. 模型参数输出：输出训练好的模型的截距和系数。
8. 结果可视化：将原始数据和模型拟合的直线进行绘制。

通过上述过程，我们可以得到一个简单的线性回归模型，并可视化其拟合效果。这种模型在实际应用中具有广泛的用途，如预测房价、分析市场趋势等。尽管线性回归模型相对简单，但其背后的原理和方法为更复杂的模型奠定了基础，因此深入理解线性回归对学习其他机器学习算法具有重要意义。

2.2 逻辑回归

逻辑回归（Logistic Regression）是一种常用于二分类问题的监督学习算法。尽管名字中带有“回归”，逻辑回归实际是一种分类方法。它通过学习数据特征与目标变量之间的关系，预测目标变量属于某个类别的概率。

2.2.1 逻辑回归简介

逻辑回归的核心思想是使用逻辑函数（Logistic Function），又称为Sigmoid函数，将线性回归的输出映射到0和1之间的概率值。逻辑函数的数学表达式为：

2.2.2 逻辑回归的假设

1. 线性可分性：逻辑回归假设特征与对数几率（log-odds）之间存在线性关系。
2. 独立性：样本彼此独立。
3. 同方差性：输入特征对目标变量的影响是恒定的。

2.2.3 逻辑回归的损失函数

逻辑回归使用对数损失函数（Log Loss）来衡量预测值与真实值之间的差异，其形式为：

2.2.4 代码实现

以下是使用Python和PyTorch实现逻辑回归的示例代码：

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt

# 生成样本数据
np.random.seed(0)
X = np.random.rand(100, 2)
y = (X[:, 0] + X[:, 1] > 1).astype(np.float32).reshape(-1, 1)

# 将数据转换为PyTorch张量
X_tensor = torch.tensor(X, dtype=torch.float32)
y_tensor = torch.tensor(y, dtype=torch.float32)

# 定义逻辑回归模型
class LogisticRegressionModel(nn.Module):
    def __init__(self):
        super(LogisticRegressionModel, self).__init__()
        self.linear = nn.Linear(2, 1)
    
    def forward(self, x):
        return torch.sigmoid(self.linear(x))

# 创建模型实例
model = LogisticRegressionModel()

# 定义损失函数和优化器
criterion = nn.BCELoss()  # 二分类交叉熵损失
optimizer = optim.SGD(model.parameters(), lr=0.1)

# 训练模型
num_epochs = 1000
for epoch in range(num_epochs):
    model.train()
    optimizer.zero_grad()
    outputs = model(X_tensor)
    loss = criterion(outputs, y_tensor)
    loss.backward()
    optimizer.step()
    
    if (epoch+1) % 100 == 0:
        print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')

# 打印模型参数
print(f'Intercept (b0): {model.linear.bias.item():.4f}')
print(f'Coefficients (b1, b2): {model.linear.weight.data.numpy()}')

# 可视化结果
model.eval()
with torch.no_grad():
    plt.scatter(X[y.flatten() == 0][:, 0], X[y.flatten() == 0][:, 1], color='red', label='Class 0')
    plt.scatter(X[y.flatten() == 1][:, 0], X[y.flatten() == 1][:, 1], color='blue', label='Class 1')
    x1_min, x1_max = X[:, 0].min(), X[:, 0].max()
    x2_min, x2_max = X[:, 1].min(), X[:, 1].max()
    xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max, 100), np.linspace(x2_min, x2_max, 100))
    grid = torch.tensor(np.c_[xx1.ravel(), xx2.ravel()], dtype=torch.float32)
    probs = model(grid).reshape(xx1.shape)
    plt.contour(xx1, xx2, probs, levels=[0.5], cmap="Greys", vmin=0, vmax=.6)
    plt.xlabel('Feature 1')
    plt.ylabel('Feature 2')
    plt.legend()
    plt.show()

代码解释：

1. 数据生成：生成两个特征，目标变量根据特征和设定的条件生成二分类标签。
2. 数据转换：将生成的numpy数组转换为PyTorch张量，便于后续处理。
3. 模型定义：定义一个包含线性层和Sigmoid激活函数的逻辑回归模型。
4. 模型实例化：创建模型实例。
5. 损失函数和优化器：使用二分类交叉熵损失函数（BCELoss）和随机梯度下降（SGD）优化器。
6. 模型训练：进行1000次迭代，每次迭代中计算预测值、损失，反向传播并更新模型参数。
7. 模型参数输出：输出训练好的模型的截距和系数。
8. 结果可视化：将原始数据和模型的决策边界进行绘制。

通过上述过程，我们可以得到一个简单的逻辑回归模型，并可视化其决策边界。逻辑回归模型在二分类任务中具有广泛的应用，如垃圾邮件检测、癌症诊断等。尽管逻辑回归模型相对简单，但其在很多实际问题中仍然表现出色，并且为理解更复杂的分类算法奠定了基础。

2.3 决策树

决策树（Decision Tree）是一种常用的监督学习算法，可以用于回归和分类任务。决策树模型通过学习数据中的决策规则，将数据分割成不同的分支和叶子节点，从而实现预测目标变量的目的。决策树的结构类似于树状图，由根节点、内部节点和叶子节点组成，每个节点代表一个特征的决策。

2.3.1 决策树简介

决策树模型通过一系列的“是/否”问题将数据逐步分割，直至每个叶子节点包含相对纯净的数据。这种分割方式使得决策树具有很强的解释性，因为每个分割步骤都可以用简单的规则描述。

2.3.2 决策树构建过程

决策树的构建过程主要包括以下几个步骤：

1. 选择最佳分割点：在当前节点上选择一个特征及其分割点，使得数据按照该特征分割后，目标变量的纯净度最大化。
2. 递归分割数据：将数据按照选择的分割点分割成两部分，并对每部分数据重复上述步骤，直到满足停止条件（如达到最大深度或叶子节点纯净度足够高）。
3. 生成叶子节点：当无法进一步分割数据时，生成叶子节点，并将该节点的输出设为其包含数据的多数类（分类任务）或均值（回归任务）。

2.3.3 纯净度指标

在选择最佳分割点时，通常使用纯净度指标来衡量分割效果。常见的纯净度指标包括：

• 信息增益（Information Gain）：基于熵（Entropy）的变化量来衡量分割前后数据纯净度的变化。熵越小，数据越纯净。
• 基尼指数（Gini Index）：基于概率的平方和来衡量数据的纯净度。基尼指数越小，数据越纯净。
• 均方误差（Mean Squared Error, MSE）：用于回归任务，衡量预测值与真实值之间的均方差。

2.3.4 决策树的优缺点

优点：

• 易于理解和解释：决策树模型可以通过图形化的树状结构直观展示决策过程。
• 无需特征缩放：决策树对数据的缩放不敏感，适用于原始数据。
• 处理多类别问题：决策树可以同时处理多类别分类问题。

缺点：

• 容易过拟合：决策树在训练过程中容易过拟合，特别是当树的深度很大时。
• 对数据变化敏感：决策树对数据中的噪声和变化非常敏感，可能导致树结构的不稳定。
• 计算复杂度高：当特征和样本数量较大时，决策树的构建和预测速度较慢。

2.3.5 代码实现

以下是使用Python和Scikit-learn库实现决策树分类器的示例代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree

# 加载数据集
iris = load_iris()
X = iris.data[:, 2:]  # 选择花瓣长度和宽度两个特征
y = iris.target

# 拆分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 创建决策树分类器
clf = DecisionTreeClassifier(criterion='gini', max_depth=4, random_state=42)

# 训练模型
clf.fit(X_train, y_train)

# 预测测试集
y_pred = clf.predict(X_test)

# 输出模型准确率
accuracy = np.mean(y_pred == y_test)
print(f'Accuracy: {accuracy:.4f}')

# 可视化决策树
plt.figure(figsize=(12,8))
tree.plot_tree(clf, filled=True, feature_names=iris.feature_names[2:], class_names=iris.target_names)
plt.show()

代码解释：

1. 数据加载：加载Iris数据集，并选择花瓣长度和宽度作为特征。
2. 数据拆分：将数据集拆分为训练集和测试集。
3. 模型创建：创建决策树分类器，并设置纯净度指标为基尼指数，最大深度为4。
4. 模型训练：使用训练集数据训练模型。
5. 模型预测：使用测试集数据进行预测，并计算模型的准确率。
6. 决策树可视化：使用Matplotlib和Scikit-learn中的plot_tree函数可视化决策树结构。

决策树剪枝

为了减少过拟合问题，可以对决策树进行剪枝（Pruning）。剪枝分为预剪枝（Pre-pruning）和后剪枝（Post-pruning）两种方法：

• 预剪枝：在构建决策树的过程中，通过设置参数（如最大深度、最小样本分割数等）提前停止分割。
• 后剪枝：在构建完整决策树后，通过移除不重要的节点来简化树结构。

在实际应用中，合理设置剪枝参数可以显著提高决策树模型的泛化能力。

2.3.6 决策树的应用场景

决策树在许多实际应用中表现出色，以下是几个典型的应用场景：

• 医疗诊断：通过分析患者的症状和体征，决策树可以辅助医生进行疾病诊断。
• 客户细分：在市场营销中，通过客户行为和特征进行细分，帮助制定针对性的营销策略。
• 金融风险管理：在信用评分和风险评估中，通过客户的历史数据预测违约风险。

决策树模型凭借其直观性和强大的分类能力，在多个领域都得到了广泛应用。虽然决策树有一些局限性，但通过适当的优化和剪枝技术，决策树仍然是一个非常有效的机器学习工具。

2.4 支持向量机

支持向量机（Support Vector Machine, SVM）是一种强大的监督学习算法，广泛应用于分类和回归任务。SVM的核心思想是通过寻找一个最优超平面来将数据点划分到不同的类别中，从而实现分类的目的。支持向量机在高维特征空间中表现优异，特别适合处理线性不可分的数据集。

2.4.1 支持向量机简介

支持向量机旨在找到一个能够最大化类间间隔（margin）的决策边界。决策边界可以是线性的，也可以通过核函数（Kernel Function）映射到高维空间，从而处理非线性分类问题。SVM通过以下公式定义决策超平面：

2.4.2 支持向量机的优化目标

支持向量机的优化目标是最大化类间间隔（margin），即最小化以下损失函数：

2.4.3 核函数

为了处理线性不可分的数据，支持向量机引入了核函数，将原始数据映射到高维特征空间。在高维空间中，数据有更高的概率可以被线性分割。常见的核函数包括：

2.4.4 支持向量机的优缺点

优点：

• 有效处理高维数据：SVM在高维特征空间中表现优异，适用于维度较高的数据集。
• 鲁棒性强：在少量样本的情况下，SVM依然能够表现出色。
• 明确的几何解释：SVM通过最大化类间间隔，具有明确的几何解释。

缺点：

• 计算复杂度高：SVM的训练过程涉及二次规划问题，对计算资源要求较高。
• 对参数敏感：SVM的性能对核函数和超参数（如 ( C ) 和 ( \gamma )）较为敏感，需要仔细调参。
• 难以处理大规模数据集：在大规模数据集上，SVM的训练时间较长。

2.4.5 代码实现

以下是使用Python和Scikit-learn库实现支持向量机分类器的示例代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC

# 加载数据集
iris = datasets.load_iris()
X = iris.data[:, :2]  # 选择前两个特征
y = iris.target

# 将数据集分为二分类问题
X = X[y != 2]
y = y[y != 2]

# 拆分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 创建SVM分类器
clf = SVC(kernel='linear', C=1.0, random_state=42)

# 训练模型
clf.fit(X_train, y_train)

# 预测测试集
y_pred = clf.predict(X_test)

# 输出模型准确率
accuracy = np.mean(y_pred == y_test)
print(f'Accuracy: {accuracy:.4f}')

# 可视化决策边界
def plot_decision_boundary(X, y, model):
    h = .02  # 网格步长
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))
    Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired, edgecolors='k', s=20)
    plt.xlabel('Feature 1')
    plt.ylabel('Feature 2')
    plt.title('SVM Decision Boundary')
    plt.show()

plot_decision_boundary(X, y, clf)

代码解释：

1. 数据加载：加载Iris数据集，并选择前两个特征用于分类。
2. 数据处理：将数据集转化为二分类问题，以便于SVM处理。
3. 数据拆分：将数据集拆分为训练集和测试集。
4. 模型创建：创建线性核SVM分类器，并设置正则化参数 ( C ) 为1.0。
5. 模型训练：使用训练集数据训练模型。
6. 模型预测：使用测试集数据进行预测，并计算模型的准确率。
7. 决策边界可视化：通过绘制决策边界和数据点，直观展示SVM分类器的效果。

2.4.6 支持向量机的应用场景

支持向量机在许多实际应用中表现出色，以下是几个典型的应用场景：

• 文本分类：SVM在垃圾邮件检测、情感分析等文本分类任务中广泛应用。
• 图像识别：在手写数字识别、面部识别等图像分类任务中，SVM表现优异。
• 生物信息学：SVM用于基因表达数据分析、蛋白质分类等生物信息学任务。

支持向量机模型凭借其高效的分类能力和坚实的理论基础，在多个领域得到了广泛应用。虽然SVM在处理大规模数据集时面临挑战，但通过适当的优化和核函数选择，SVM仍然是一个非常强大的机器学习工具。

2.5 K近邻

K近邻（K-Nearest Neighbors, KNN）是一种简单而有效的非参数监督学习算法，广泛应用于分类和回归任务。KNN算法通过计算新样本与训练集样本之间的距离，找到距离最近的K个邻居，基于这些邻居的标签来预测新样本的标签。

2.5.1 K近邻简介

K近邻算法的核心思想是“物以类聚，人以群分”，即相似的数据点更可能属于同一类。在分类任务中，KNN通过统计K个最近邻居中各类别的频率，选择出现次数最多的类别作为预测结果；在回归任务中，KNN通过计算K个最近邻居的平均值来进行预测。

2.5.2 距离度量

K近邻算法的关键在于如何度量数据点之间的距离。常见的距离度量方法包括：

2.5.3 选择K值

选择合适的K值是KNN算法的重要步骤。K值过小可能导致模型对噪声敏感，从而导致过拟合；K值过大则可能导致模型过于平滑，忽略数据的局部结构，从而导致欠拟合。常见的选择K值的方法包括：

• 经验法则：根据经验选择一个合适的K值，通常在3到10之间。
• 交叉验证：通过交叉验证来选择最优的K值，保证模型在验证集上表现最佳。

2.5.4 K近邻的优缺点

优点：

• 简单易懂：KNN算法直观且易于理解。
• 无参数学习：KNN是无参数模型，不需要训练阶段，仅需保存训练数据。
• 适用于多类别分类：KNN可以处理多类别分类问题。

缺点：

• 计算复杂度高：每次预测都需要计算与所有训练样本的距离，计算复杂度较高。
• 对数据规模敏感：大规模数据集上，KNN的计算和存储开销较大。
• 对特征缩放敏感：不同量纲的特征会影响距离计算结果，需要进行特征缩放。

2.5.5 代码实现

以下是使用Python和Scikit-learn库实现K近邻分类器的示例代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score

# 加载数据集
iris = datasets.load_iris()
X = iris.data[:, :2]  # 选择前两个特征
y = iris.target

# 拆分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 特征缩放
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# 创建KNN分类器
k = 5  # 选择K值
knn = KNeighborsClassifier(n_neighbors=k)

# 训练模型
knn.fit(X_train, y_train)

# 预测测试集
y_pred = knn.predict(X_test)

# 输出模型准确率
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.4f}')

# 可视化决策边界
def plot_decision_boundary(X, y, model):
    h = .02  # 网格步长
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))
    Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired, edgecolors='k', s=20)
    plt.xlabel('Feature 1')
    plt.ylabel('Feature 2')
    plt.title(f'KNN Decision Boundary (k={k})')
    plt.show()

plot_decision_boundary(X_test, y_test, knn)

代码解释：

1. 数据加载：加载Iris数据集，并选择前两个特征用于分类。
2. 数据拆分：将数据集拆分为训练集和测试集。
3. 特征缩放：对数据进行标准化处理，以消除不同特征量纲的影响。
4. 模型创建：创建K近邻分类器，并选择K值为5。
5. 模型训练：使用训练集数据训练模型。
6. 模型预测：使用测试集数据进行预测，并计算模型的准确率。
7. 决策边界可视化：通过绘制决策边界和数据点，直观展示KNN分类器的效果。

2.5.6 K近邻的应用场景

K近邻算法在许多实际应用中表现出色，以下是几个典型的应用场景：

• 推荐系统：通过计算用户的相似度，为用户推荐相似的商品或内容。
• 图像识别：在手写数字识别、面部识别等图像分类任务中，KNN表现良好。
• 文本分类：在垃圾邮件检测、情感分析等文本分类任务中，KNN广泛应用。

K近邻算法凭借其简单直观和有效性，在多个领域得到了广泛应用。虽然KNN在处理大规模数据集时面临挑战，但通过优化和合适的距离度量方法，KNN仍然是一个非常有用的机器学习工具。

监督学习精讲

2. 常见算法

2.6 朴素贝叶斯

朴素贝叶斯（Naive Bayes）是一种基于贝叶斯定理的监督学习算法，广泛应用于分类任务。尽管其假设各特征之间相互独立且同等重要，这一“朴素”假设在很多实际问题中并不成立，但朴素贝叶斯仍然在许多应用中表现出色，尤其是文本分类问题。

2.6.1 朴素贝叶斯简介

朴素贝叶斯算法基于贝叶斯定理进行分类预测。贝叶斯定理的数学表达式为：

2.6.2 朴素贝叶斯的类型

朴素贝叶斯分类器有多种类型，主要根据特征值的不同分布假设进行分类：

• 高斯朴素贝叶斯（Gaussian Naive Bayes）：假设特征值服从高斯分布，适用于连续数据。
• 多项式朴素贝叶斯（Multinomial Naive Bayes）：假设特征值服从多项式分布，适用于离散数据，特别是文本分类中的词频统计。
• 伯努利朴素贝叶斯（Bernoulli Naive Bayes）：假设特征值服从伯努利分布，适用于二元数据，特别是文本分类中的词是否出现。

2.6.3 朴素贝叶斯的优缺点

优点：

• 简单高效：朴素贝叶斯算法计算复杂度低，易于实现，适用于大规模数据集。
• 处理缺失数据：朴素贝叶斯能够处理部分特征缺失的数据。
• 适用于多类别分类：朴素贝叶斯能够自然处理多类别分类问题。

缺点：

• 独立性假设：朴素贝叶斯假设特征之间相互独立，这在许多实际问题中并不成立。
• 零概率问题：如果某个特征值在训练集中未出现，可能导致零概率问题，需要拉普拉斯平滑（Laplace Smoothing）来处理。

2.6.4 代码实现

以下是使用Python和Scikit-learn库实现朴素贝叶斯分类器的示例代码：

import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report

# 加载数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target

# 拆分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 创建高斯朴素贝叶斯分类器
gnb = GaussianNB()

# 训练模型
gnb.fit(X_train, y_train)

# 预测测试集
y_pred = gnb.predict(X_test)

# 输出模型准确率
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.4f}')

# 输出混淆矩阵和分类报告
print("Confusion Matrix:")
print(confusion_matrix(y_test, y_pred))
print("\nClassification Report:")
print(classification_report(y_test, y_pred))

代码解释：

1. 数据加载：加载Iris数据集，包括所有四个特征。
2. 数据拆分：将数据集拆分为训练集和测试集。
3. 模型创建：创建高斯朴素贝叶斯分类器实例。
4. 模型训练：使用训练集数据训练模型。
5. 模型预测：使用测试集数据进行预测，并计算模型的准确率。
6. 评估模型：输出混淆矩阵和分类报告，以详细评估模型性能。

2.6.5 朴素贝叶斯的应用场景

朴素贝叶斯在许多实际应用中表现出色，以下是几个典型的应用场景：

• 文本分类：朴素贝叶斯广泛应用于垃圾邮件检测、情感分析、新闻分类等文本分类任务。
• 医学诊断：在疾病诊断和风险预测中，朴素贝叶斯可以根据症状和体征进行分类。
• 推荐系统：朴素贝叶斯用于推荐系统中，基于用户行为和特征进行个性化推荐。

朴素贝叶斯算法凭借其简单高效和适用广泛，在多个领域得到了广泛应用。尽管其假设存在一定局限性，但通过适当的改进和优化，朴素贝叶斯仍然是一个非常有用的机器学习工具。

监督学习精讲

3. 模型评估与验证

在机器学习过程中，模型评估与验证是至关重要的环节。通过评估，我们能够了解模型的性能，判断其是否适合解决特定的问题；通过验证，我们能够检测模型是否泛化良好，是否能够在未见过的数据上表现出色。有效的模型评估与验证能够帮助我们选择最优模型并防止过拟合和欠拟合。

3.1 交叉验证

交叉验证（Cross-Validation）是一种评估模型性能的技术，它通过将数据集分成多个子集，并多次训练和验证模型来评估模型的性能。最常用的交叉验证方法是K折交叉验证（K-Fold Cross-Validation）。

3.1.1 K折交叉验证

K折交叉验证将数据集分成K个大小相等的子集，每次选择一个子集作为验证集，其余K-1个子集作为训练集，重复K次，最终计算K次验证的平均性能作为模型的评估结果。K折交叉验证的具体步骤如下：

1. 将数据集随机分成K个大小相等的子集。
2. 对于每个子集：
   • 将该子集作为验证集，其余子集作为训练集。
   • 训练模型并在验证集上评估模型性能。
3. 计算所有K次评估的平均性能。

K折交叉验证能够有效缓解由于数据集划分带来的偶然性影响，提高评估结果的可靠性。常用的K值有5和10。

3.1.2 留一法交叉验证

留一法交叉验证（Leave-One-Out Cross-Validation, LOOCV）是一种极端的交叉验证方法，每次只用一个样本作为验证集，剩余样本作为训练集，重复N次（N为样本数量），最终计算N次评估的平均性能。尽管LOOCV的评估结果较为稳定，但计算开销较大，通常在小数据集上使用。

3.2 过拟合与欠拟合

过拟合（Overfitting）和欠拟合（Underfitting）是机器学习中的常见问题，直接影响模型的泛化能力。

3.2.1 过拟合

过拟合是指模型在训练数据上表现很好，但在验证数据上表现较差。这是因为模型过于复杂，捕捉到了训练数据中的噪声和细节，而没有学到数据的普遍规律。过拟合的常见原因包括：

• 模型复杂度过高
• 训练数据量不足
• 过度训练（训练次数过多）

解决过拟合的方法包括：

• 降低模型复杂度（如减少特征数量或使用正则化）
• 增加训练数据量
• 使用交叉验证选择合适的超参数
• 早停（Early Stopping）

3.2.2 欠拟合

欠拟合是指模型在训练数据和验证数据上都表现较差。这是因为模型过于简单，无法捕捉数据的内在规律。欠拟合的常见原因包括：

• 模型复杂度过低
• 特征数量不足
• 训练时间不足

解决欠拟合的方法包括：

• 增加模型复杂度（如增加特征数量或使用更复杂的模型）
• 提高特征质量
• 延长训练时间

3.3 混淆矩阵与分类报告

混淆矩阵（Confusion Matrix）是评估分类模型性能的重要工具，它能够直观地展示模型在各个类别上的分类情况。混淆矩阵的结构如下：

实际\预测	正类（Positive）	负类（Negative）
正类（Positive）	真阳性（TP）	假阴性（FN）
负类（Negative）	假阳性（FP）	真阴性（TN）

通过混淆矩阵，我们可以计算多个评价指标，包括：

分类报告（Classification Report）通常包含上述指标，可以全面评估分类模型的性能。

3.4 ROC曲线与AUC

ROC曲线（Receiver Operating Characteristic Curve）是评估二分类模型性能的工具，通过绘制真阳性率（TPR）和假阳性率（FPR）之间的关系，展示模型的区分能力。真阳性率和假阳性率的计算公式为：

通过调整分类阈值，可以绘制出不同点的TPR和FPR，形成ROC曲线。理想的ROC曲线接近左上角，表示模型具有较高的区分能力。

AUC（Area Under Curve）是ROC曲线下的面积，数值在0.5到1之间，越接近1表示模型性能越好。AUC具有阈值独立性，是衡量模型性能的有效指标。

代码示例

以下是使用Python和Scikit-learn库实现混淆矩阵、分类报告、ROC曲线和AUC的示例代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import confusion_matrix, classification_report, roc_curve, auc

# 加载数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target

# 将数据集分为二分类问题
X = X[y != 2]
y = y[y != 2]

# 拆分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 创建高斯朴素贝叶斯分类器
gnb = GaussianNB()

# 训练模型
gnb.fit(X_train, y_train)

# 预测测试集
y_pred = gnb.predict(X_test)
y_prob = gnb.predict_proba(X_test)[:, 1]

# 输出混淆矩阵和分类报告
print("Confusion Matrix:")
print(confusion_matrix(y_test, y_pred))
print("\nClassification Report:")
print(classification_report(y_test, y_pred))

# 绘制ROC曲线
fpr, tpr, _ = roc_curve(y_test, y_prob)
roc_auc = auc(fpr, tpr)

plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (area = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic (ROC)')
plt.legend(loc="lower right")
plt.show()

代码解释：

1. 数据加载和处理：加载Iris数据集，并将其转化为二分类问题。
2. 数据拆分：将数据集拆分为训练集和测试集。
3. 模型训练和预测：创建并训练高斯朴素贝叶斯分类器，对测试集进行预测。
4. 评估模型：计算并输出混淆矩阵、分类报告、ROC曲线和AUC。

通过上述过程，我们能够全面评估分类模型的性能，判断其是否适合特定的任务。有效的模型评估与验证是机器学习流程中的重要环节，能够帮助我们选择最优模型并提高模型的泛化能力。