---

1. 作者介绍

黄雨浩，男，西安工程大学电子信息学院，2023级研究生
研究方向：机器视觉与人工智能
电子邮件：1986506577@qq.com

孙思伟，男，西安工程大学电子信息学院，2023级研究生，张宏伟人工智能课题组
研究方向：深度强化学习与人工智能
电子邮件：sunsiwei0109@163.com

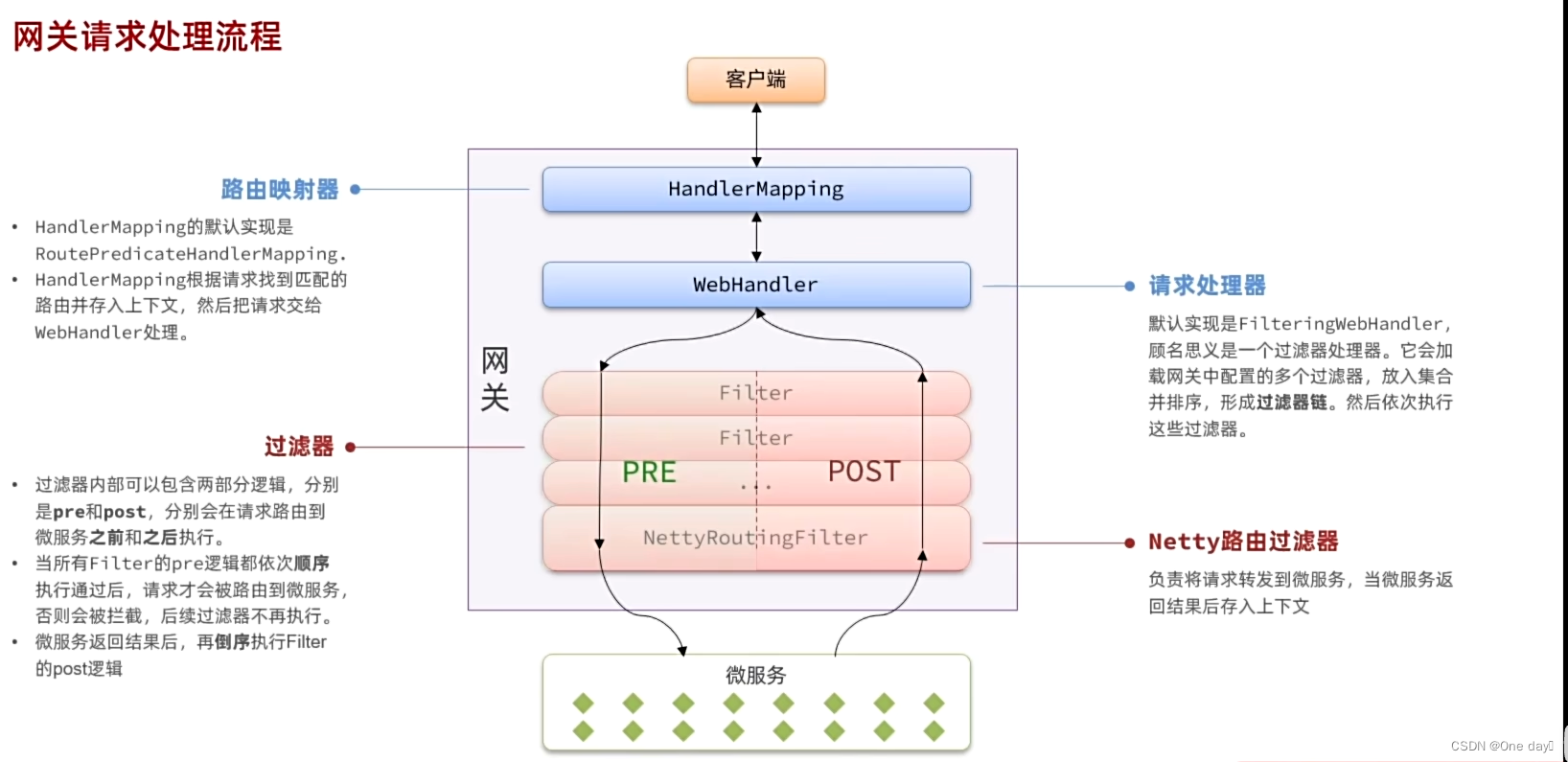
2. 多维尺度分析（Multi-Dimensional Scaling, MDS）介绍

2.1 MDS介绍

多维尺度分析（Multi-Dimensional Scaling, MDS）是一种统计学方法，用于将复杂、高维的相似性或距离数据转化为直观的、低维的可视化表示。它是通过保持原始数据中对象间距离关系的近似，将数据映射到一个较低维度的空间中，使得这些对象在新空间中的位置关系能够反映出原始数据中的相似性或距离。本质上是通过优化目标函数来实现高维到低维的映射。

2.2 MDS的类别

2.2.1度量MDS

具体来说假设原始数据中的相似性或距离度量满足三角不等式，即对于任何三个对象i、j、k，有 d_ik ≤d_ij+d_jk。在这种情况下，MDS可以通过经典线性代数方法（如奇异值分解SVD）来求解。

2.2.2非度量MDS

不假设原始数据满足度量性质，而是通过秩次排序来表示对象间的相对相似性或距离。非度量MDS通常采用迭代优化算法（如SMACOF算法）来逼近最优解。

2.3 目标函数

目标函数通常包含两个部分：一是保持原始数据中对象间距离的近似度（stress函数），二是映射到低维空间的约束条件。具体来说，MDS试图找到一个低维空间中的点阵P，使得P中各点之间的距离与原始数据中对应对象间的相似性或距离度量尽可能接近。优化过程通常涉及最小化以下形式的目标函数：

d_ij表示原始数据中对象i和j之间的相似性或距离度量，p_i,p_j分别为它们在低维空间中的坐标向量。通过最小化stress函数S§，MDS力求在低维空间中保持原始数据的距离结构。

2.4 MDS降维计算步骤

2.4.1计算流程

2.4.2 算法示例

假设有5种水果：苹果（A）、香蕉（B）、橙子（C）、葡萄（D）和菠萝（E）。对这些水果进行了甜度（Sweetness）、酸度（Sourness）和多汁程度（Juiciness）的评分。

第一步：计算距离
使用欧式距离计算

A-B: 4.69 A-C: 3.74 A-D: 2.45 A-E: 3.32 B-C: 6.56 B-D: 3.32 B-E: 6.56 C-D: 5.29 C-E: 2.45 D-E: 5.29

第二步：构建距离矩阵

第三步：中心化距离矩阵
计算中心化矩阵H，数据点的数量n为5

第五步：计算特征值和特征向量

第六步：计算降维后坐标
构建特征向量矩阵V和特征值矩阵Λ的平方根；然后，我们计算降维后的坐标：新坐标 = A * A^(1/2)

最后完成降维

3．实验过程

3.1数据集介绍

Boston数据集是一个经典的回归分析数据集，包含了美国波士顿地区的房价数据以及相关的属性信息。该数据集共有506个样本，14个属性，其中包括13个特征变量和1个目标变量（房价中位数）。

序号	英文	中文
1	CRIM per capita crime rate by town	城镇人均犯罪率
2	ZN proportion of residential land zoned for lots over 25,000 sq.ft.	住宅用地所占比例，25000英尺
3	INDUS proportion of non-retail business acres per town	城镇中非商业用地的所占比例
4	CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)	CHAS查尔斯河虚拟变量，用于回归分析
5	NOX nitric oxides concentration (parts per 10 million)	环保指标
6	RM average number of rooms per dwelling	每栋住宅的房间数
7	AGE proportion of owner-occupied units built prior to 1940	1940年以前建成的自住单位的比例
8	DIS weighted distances to five Boston employment centres	距离五个波士顿就业中心的加权距离
9	RAD index of accessibility to radial highways	距离高速公路的便利指数
10	TAX full-value property-tax rate per $10,000	每一万美元的不动产税率
11	PTRATIO pupil-teacher ratio by town	城镇中教师学生比例
12	B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town	城镇中黑人的比例
13	LSTAT % lower status of the population	地区有多少百分比的房东属于低收入阶层
14	MEDV Median value of owner-occupied homes in $1000’s	自住房屋房价的中位数

表1 数据集包含属性

3.2算法思路

图3 MDS降维步骤

3.3算法评价

优点：
直观可视化：MDS能够将高维数据映射到二维或三维空间，便于直观地观察数据分布和结构。
保持距离关系：MDS在低维空间中尽可能保留了原始数据的距离结构，有助于发现潜在的聚类或模式。
适用范围广：无论是度量还是非度量数据，MDS都能找到合适的处理方法。
缺点：
对距离矩阵依赖性强：MDS结果的可靠性很大程度上取决于输入的距离矩阵的质量。若距离矩阵计算不当或含有噪声，可能导致映射结果失真。
计算复杂度较高：对于大规模数据集，尤其是非度量MDS，优化过程可能较为耗时。
解释性有限：虽然MDS能够生成可视化结果，但对于映射到低维空间后的具体坐标值，其物理或实际意义可能不明确。

3.4与其他降维算法相比

3.4.1主成分分析

与PCA对比：主成分分析（PCA）也是一种降维方法，但其目标是最大化数据方差的保留，而非保持距离关系。PCA更适合于线性相关性强的数据集，而MDS对非线性关系的处理能力更强。

3.4.2 t-SNE

与t-SNE对比：t-distributed Stochastic Neighbor Embedding（t-SNE）也是一种流行的降维可视化方法，其特点是擅长揭示高维数据的局部结构。相比MDS，t-SNE对局部聚类效果更好，但全局结构可能不如MDS清晰。

3.5代码实现

3.5.1二维可视化代码

import numpy as np
import pandas as pd
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.manifold import MDS
import matplotlib.pyplot as plt

# 加载波士顿房价数据集
boston = load_boston()
X = boston.data
y = boston.target

# 对特征进行标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 使用MDS进行降维
mds = MDS(n_components=2)  # 设置要降维到的目标维度为2
X_mds = mds.fit_transform(X_scaled)

# 可视化降维前的数据
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=y, cmap='viridis')
plt.title('Original Data')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')

# 可视化降维后的数据
plt.subplot(1, 2, 2)
plt.scatter(X_mds[:, 0], X_mds[:, 1], c=y, cmap='viridis')
plt.title('MDS Reduced Data')
plt.xlabel('Component 1')
plt.ylabel('Component 2')

plt.tight_layout()
plt.show()

3.5.2三维可视化代码

# 可视化降维后的数据
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X_mds[:, 0], X_mds[:, 1], X_mds[:, 2], c=y, cmap='viridis')
ax.set_title('MDS Reduced Data (3D)')
ax.set_xlabel('Component 1')
ax.set_ylabel('Component 2')
ax.set_zlabel('Component 3')

3.6实验结果

图4 MDS降维降为二维结果

图5 MDS降维降为三维结果

4. 参考连接

1. 深度探索：机器学习多维尺度（MDS）算法原理及其应用
2. 多尺度变换（Multidimensional Scaling ，MDS）详解