题干：

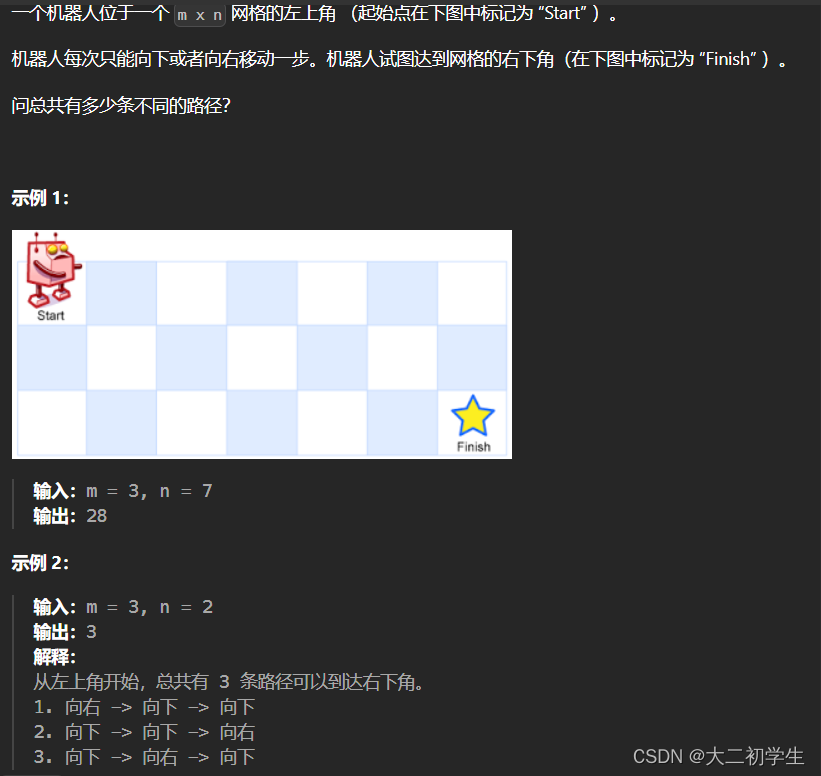
代码：

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>>dp(m,vector<int>(n, 0));
        for(int i = 0; i < m; i++) dp[i][0] = 1;
        for(int j = 0; j < n; j++) dp[0][j] = 1;
        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
};

m是竖行(i)，n是横行(j)，最终到（m-1，n-1）

dp数组含义：设定二维数组dp[i][j]，代表从（0，0）出发到（i，j）有dp[i][j]种路径。

递推公式：由于只能向右/向下，所以（i，j）位置一定来自于左边(i, j-1)或上面(i-1, j)，所以dp[i][j]=dp[i-1][j]+dp[i][j-1]。

初始化：从（0，0）开始，到（i，0）的dp[i][0]肯定是1，dp[0][j]也一样。dp[i][0]=dp[0][j]。

遍历顺序：从（0，0）开始，从上到下i和从左到右j两层循环嵌套。

二维数组创建：vector<vector<int>>dp(m,vector<int>(n, 0));（创建m个横行，每个横行填入大小为n默认值为0的数组。