从一个题目引出位图
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中?
这里有两种大家容易想到的解法:
1.遍历搜索,时间复杂度为O(N)
2.先排序(O(NlogN)) ,然后利用二分查找搜索(O(logN))
上面两种方法虽然简单,但是一方面是需要的时间太久,一个内存可能没有这么大的空间用来开辟40亿个无符号整数。若是我们要将这些数全部加载到内存当中,那么将会占用16G的空间。
3.位图解决
数据是否在给定的整形数据中,结果是在或者不在,刚好是两种状态,那么可以使用一个二进制比特来代表数据是否存在的信息,如果二进制比特位为1,代表存在;如果为0,代表不存在,比如:
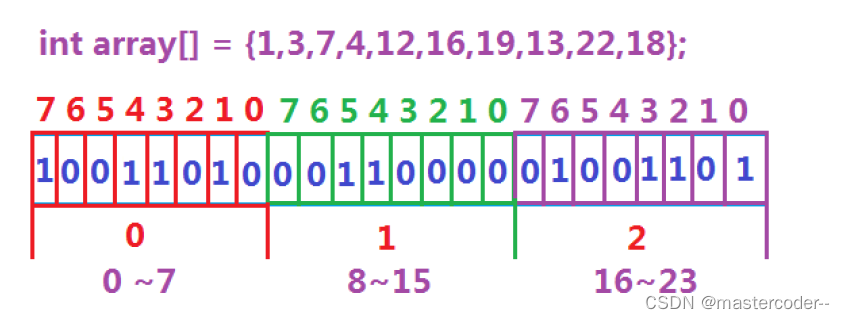
无符号整数总共有2^32个,因此记录这些数字就需要2^32个比特位,也就是512M的内存空间,内存消耗大大减少。
这里就引出位图的概念:
位图的概念
位图,就是用每一位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用来判断某个数据存不存在的。
位图的构造函数
构造函数一般可以直接复用reset函数进行实现:
第一种: N/32 + 1
首先要知道,一个整形int有32位,所以我们用数据个数直接除32即可。但是,假如N为33,多出来的1位就会没位置放了,所以一般这里会多预留一个32位,也就是+1
第二种:(N>>5) + 1
这里使用到了移位运算符>>和<<,这里的N>>5,实际上就是让数据个数从高位向低位移动,总共移动5次,也就是除以2^5,也就是除以32,这里结果是和第一种方法相同,只是方法不同。

bitset()//构造函数
{
_bits.resize(N / 32 + 1);//利用resize函数构造初始化为0
//_bits.resize((N>>5)+1);
}位图的定义
第一种:构造一个8位的位图,所有为初始化为0
bitset<8> bs1; //00000000
第二种:构造一个8位的位图,根据所给的值初始化位图前N位
bitset<8> bs2(100); //01100100第三种:构造一个8位的位图,根据字符串中的0/1序列来初始化位图的前N位
bitset<8> bs2(string("111001")); //00111001位图的set函数
set函数的使用
bitset<8> bs;
bs.set(2); //设置第2位
bs.set(4); //设置第4位
cout << bs << endl; //00010100set函数的模拟实现
方法如下:
- 计算出该位位于第 i 个整数的第 j 个比特位。
- 将1左移 j 位后与第 i 个整数进行或运算即可。(因为别的位不能受到影响)
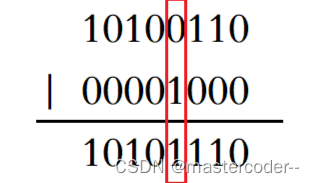
//设置位
void set(size_t x)
{
size_t i = x / 32;//先获取在第i个整数
size_t j = x % 32;//再获取在第j个位
_bits[i] |= (1 << j);//将该位设置成1
}位图的reset函数
reset函数的使用
bitset<8> bs;
bs.set(2); //设置第2位
bs.set(4); //设置第4位
cout << bs << endl; //00010100
bs.reset(2); //清空第0位
cout << bs << endl; //00010000
bs.reset(4); //清空第0位
cout << bs << endl; //00000000reset的模拟实现
方法如下:
- 计算出该位位于第 i 个整数的第 j 个比特位。
- 将1左移 j 位后与第 i 个整数进行异或运算即可。
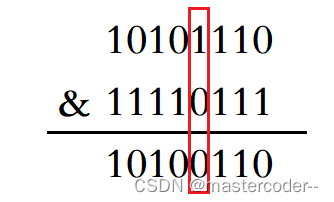
void reset(size_t x)
{
size_t = i = x / 32;//先获取在第几个整数
size_t = j = x % 32;//再获取在第几个位
_bits[i] &= (~(1 << j));//然后将该位设置成0
}