1.抗锯齿(反走样)

        在上一章中，在光栅化三角形的时候出现了明显的锯齿效果。如下图所示是三角形采样过程：

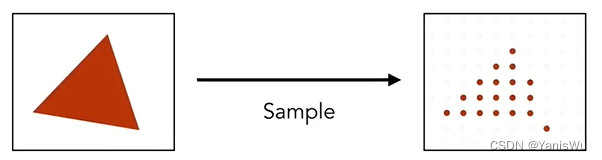
        从图上可知像素点不是纯红色就是纯白色。如果在采样前先进行模糊操作(滤波)，如下图所示：

        经过模糊操作后三角形的边缘颜色变化有了一定的过渡，再进行采样时，靠近三角形边缘的地方可以采到一部分过渡色的像素，采样结果不在是要么红色要么白色，就可以达到抗锯齿的目的。

        通过下面两张图来看使用模糊操作后的效果对比。

        再来看另外一组通过滤波处理再采样的效果。

        综上，在进行采样之前先进行模糊操作(滤波)，能够达到明显的抗锯齿效果。

2.频域与时域

        上面提到通过先进行滤波操作，再采样来达到抗锯齿的效果，叫做Blurred Aliasing。那么先进行采样，再进行滤波操作能不能同样达到抗锯齿的效果呢，答案是不行的。看下面两张图对比一下，第一张先进行采样再进行滤波操作，第二张是先进行滤波操作再进行采样，可以发现第一种操作是行不通的。

        这是为什么呢？这里需要引入频域(Frequency Domain)和时域(Spatial Domain)的概念。

        频域用来表示不同频率下信号的变化，用横轴表示频率,纵轴是该频率信号的幅度,也就是通常说的频谱图。

        时域用来表示不同时间下信号的变化，也可以表示空间上信息。用横轴表示时间,纵轴是当前时间信号的幅度。

2.1周期与频率

        下图是周期性变换的波形函数正弦和余弦函数，它们之间的不同点在于它们的相位不同。

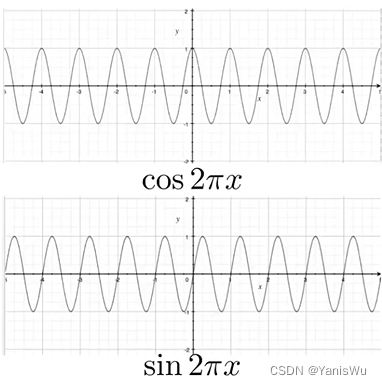
        那么使用余弦与正弦函数有啥好处呢？这里用余弦函数举例子，如下图所示：

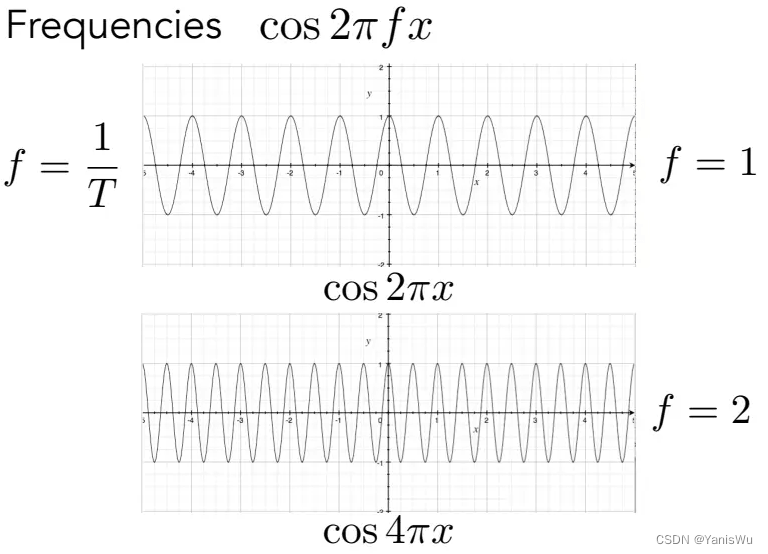
        通过余弦函数x前面的系数，会得到不同的余弦波，代表频率不同。f代表频率，频率越大代表余弦波变化越快，周期(T)越短。对于图像信号而言，我们认为两个像素间的颜色变化大则代表频率高，反之则是频率低。

2.2傅里叶变换

2.2.1傅里叶级数展开

        任何周期函数都可以用一系列正弦、余弦函数构成的线性组合以及一个常数项来表示，这种展开方式我们称为傅里叶级数展开。

        如果需要获取一个函数得到向下面这样周期变换的方波函数。

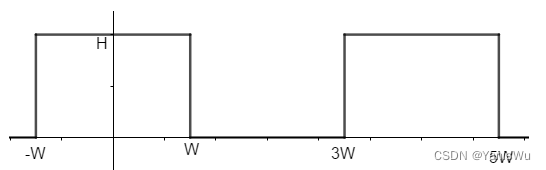
        可以首先将余弦函数振幅增加并向上移动，得到近似的周期变换函数。

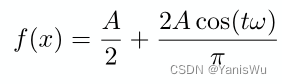
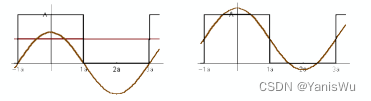
        接着加入一些函数，会更加接近这个周期函数。

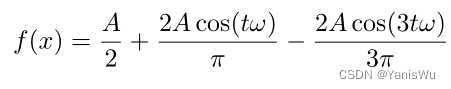
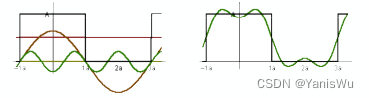
        继续加入。

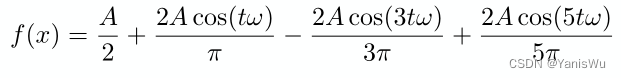
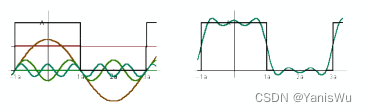
        还不够接着加入，直到周期波无限接近这个周期函数。

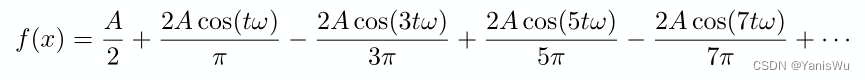
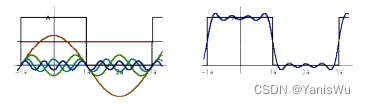
        最后，通过傅里叶级数展开，将一个目标函数展开成了多个不同频率的正弦或余弦函数。

2.2.2傅里叶变换

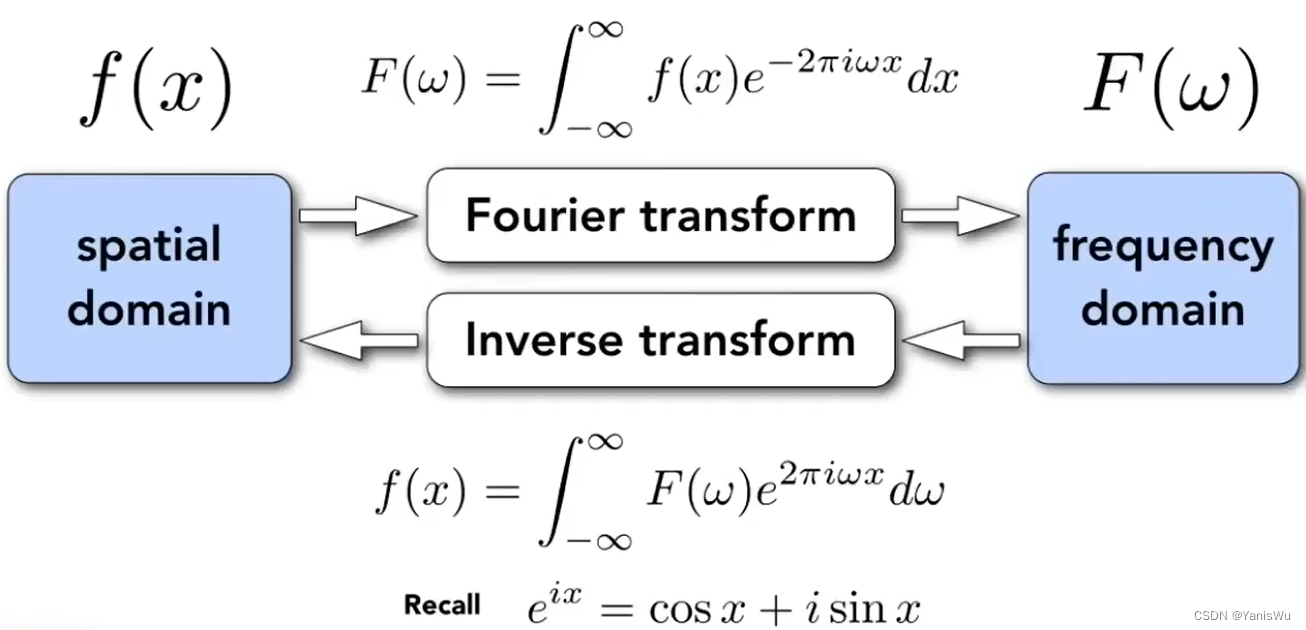
        如上图，我们可以把一个时域上的函数 f(x) 变换成频域上的函数 F(w)。称为傅里叶变换(Fourier Transform)。就是把函数变成不同频率的段，并且把不同频率的段显示出来。同时我们也可以把频域上的函数 F(w) 变换回时域上的函数 f(x) ，这个过程称为逆傅里叶变换。

2.3频率与采样

        上述中所谓傅里叶变换，就是把函数变成不同频率的段，并且把不同频率的段显示出来。这说明什么呢？先看下图所示：

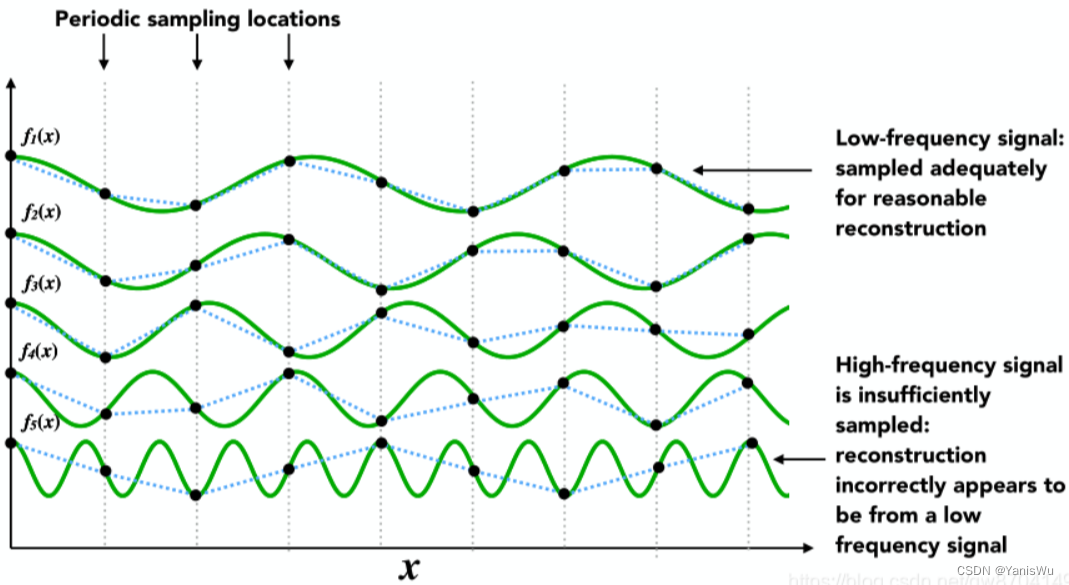
        上图中，函数 f1(x) 到f5(x) 的频率不断增加，假设我们都用完全相同的采样频率，对函数 f1(x) 采样出来的点做函数恢复(采样点相连接)，基本上可以知道原来函数的样子。同理，往下对其他函数也进行函数恢复，发现越往下函数恢复的样子离原来相差越大。也就是说当采样的频率跟不上函数本身变化的频率时，采样结果就会出现偏差，就会产生走样现象。

        比如有如下图，有一个变化剧烈的(频率大)函数。

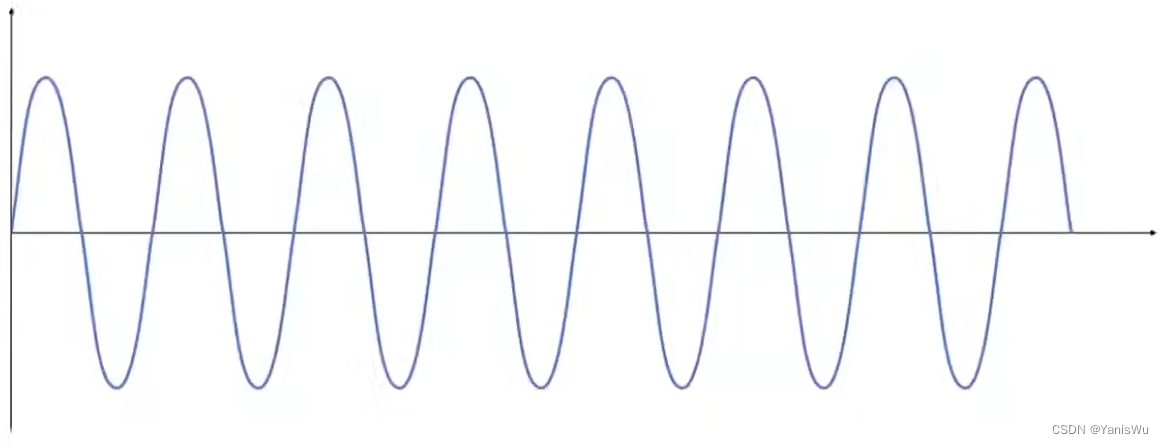
        可以按一定间隔进行采样，采样结果连成一条线。如下图所示：

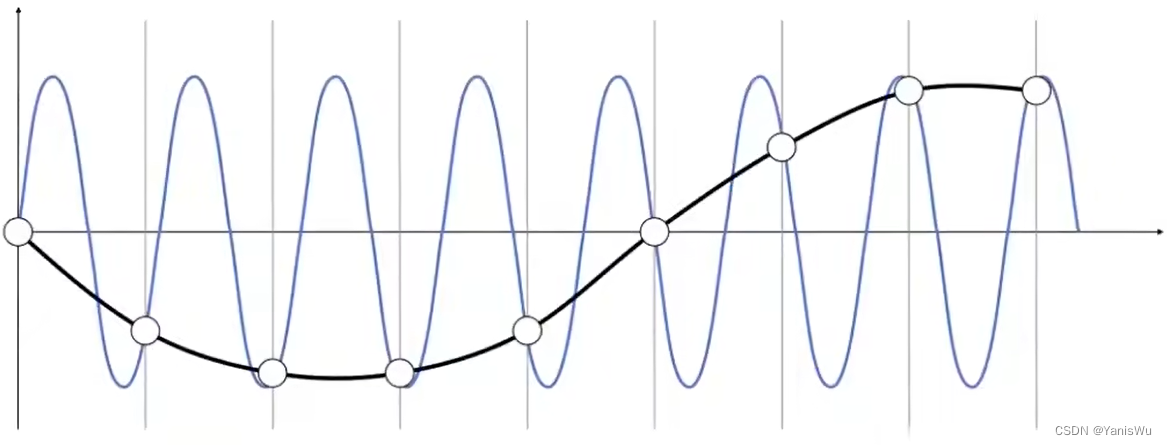
        可以发现，采样出来的函数与原本的函数相差很大。

        那么， 这里就有一个问题。假如说有两个函数，第一个是蓝色的函数，第二个是黑色的函数(假如不是恢复出来的函数，是另外一个函数)。然后用同样的采样方法，采样两种频率截然不同的信号，但是采样的结果却是完全相同的。也就是说同样的采样方法，采样两种不同频率的函数，得出的结果无法区分，这就是走样。

2.4图像与频域

        已经知道傅里叶变换就是把一个函数(信号)从时域变到频域，如下图所示。

        虽然左图中没有时间的信息，但是空间上不同的位置信息也算是时域。右图是变换的频域空间，中心表示低频区域，以这点为中心向周围扩散，越往外频率越高，在不同频率的位置上有多少信息用亮度来表示，中心比较亮，说明图片上大多是低频信息，也有部分高频信息，但相对于低频信息特别少。自然界中拍摄的图片基本都是低频信息会占据相当大的比例，而高频信息只是占了很小一部分。

        为什么右侧图里有两条特别亮的横线和竖线？图形学中分析信号的时候回认为它通常是周期性重复的，对于不周期性重复（例如一张图片，重复无限排列）就认为到了右边界之后重复左边界，左边界和右边界通常通常内容相乘较大(通常一张图片左右两边信号相差比较大)，就会产生剧烈的信号变化，也就会产生极其高的高频信号，上边界和下边界同理，所以在经过傅里叶变换的图片中会看到两条水平和垂直的比较亮的线。
        傅里叶变换可以看到一张图片中的信号在不同频率长什么样，通用的说法就是任何信号在不同频率长什么样，也称为频谱。

2.4.1滤波

        滤波(Wave filtering)是将信号中特定波段频率滤除的操作。

 2.4.1.1高通滤波

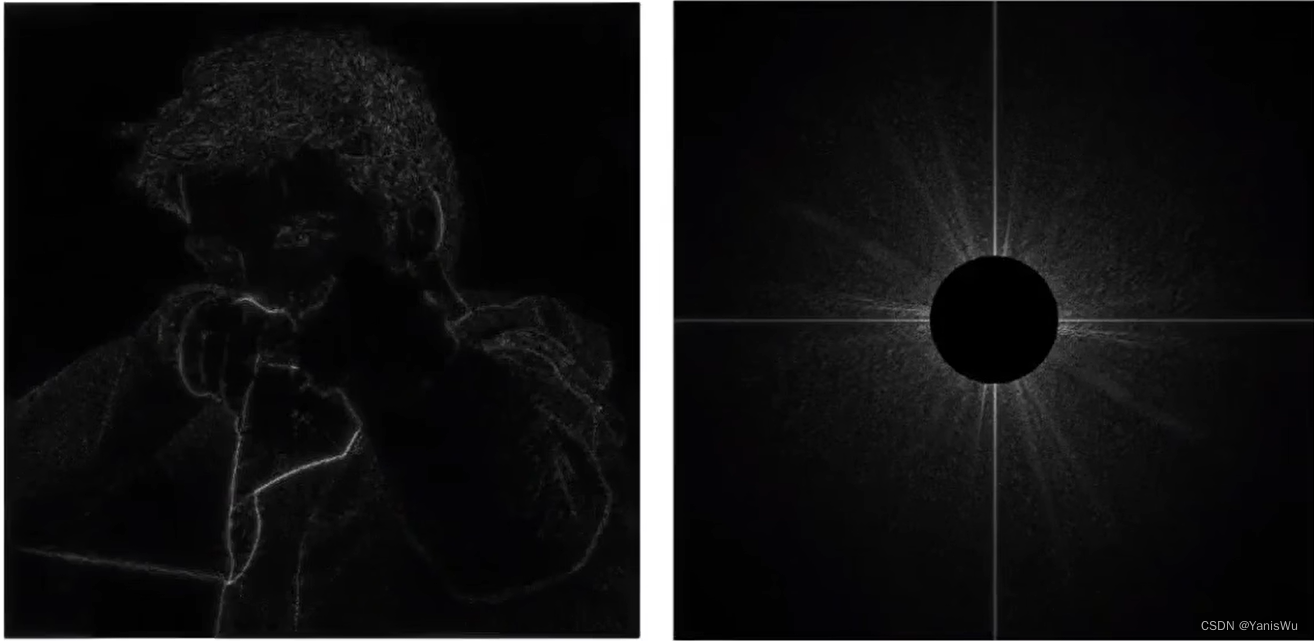
        高通滤波(High-Pass Filter)的意思就是高频信号可以通过，把低频信号过滤掉。如下图中的右侧，我们去掉低频信号，然后在通过逆傅里叶变换，得到下图中左侧的图片，可以发现高频信号其实表示的是图像中物体的边界(不是图像四边的边界，是图像内容里的边界)。

        为什么高频信号表示的是图像中物体的边界？因为在傅里叶变换前图像中物体的边界，颜色变化比较剧烈，颜色变化剧烈就会产生剧烈变化的信号，剧烈变化就会产生高频信号，所以经过傅里叶变换高频信号表示的是原图形中物体的边界。

2.4.1.2低通滤波

        低通滤波(Low-Pass Filter)的意思就是低频信号可以通过，把高频信号过滤掉，如下图右侧，把经过傅里叶变换的图像中所有的高频信号都去掉，只留下部分低频信号，在经过逆傅里叶变换就会得到下图左侧中的图像，你会发现图像变模糊了，是因为滤掉了表示图像边界的高频信号。

2.4.1.3带通滤波

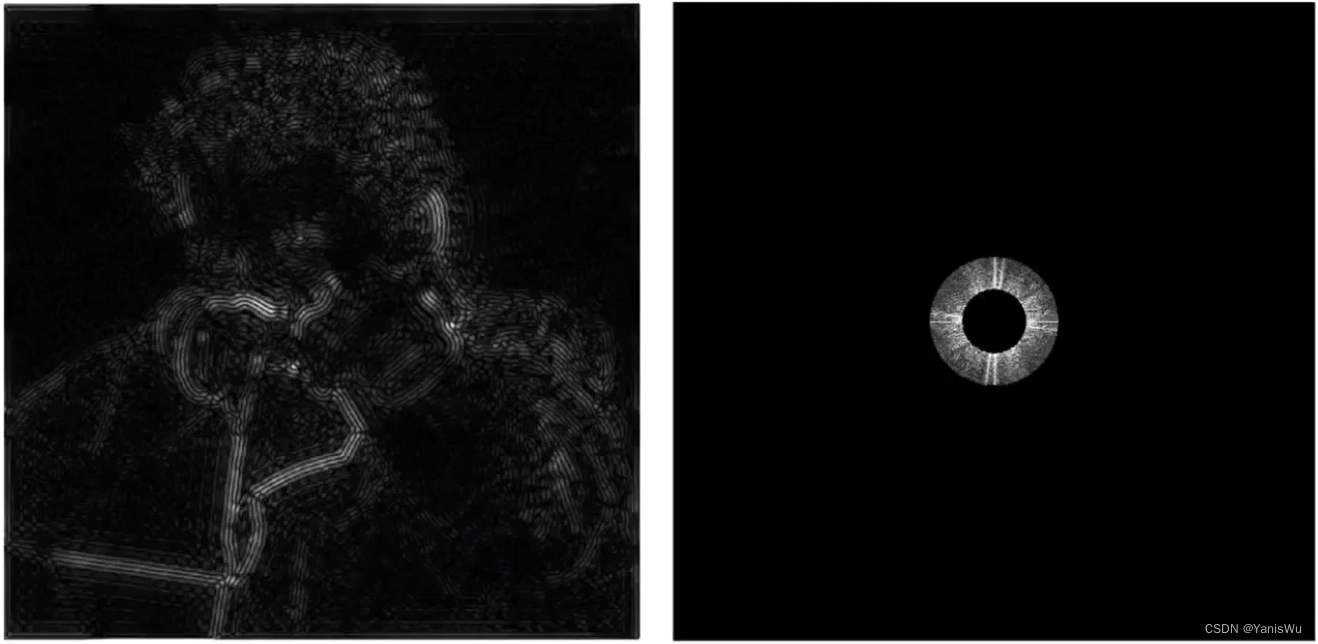
        带通滤波(Band-Pass Filter)允许限定频段的波通过，通常是将一张图片经过傅里叶变换得到频域，然后去掉高于限定的最高频和低于限定的最低频信号，如下图中右侧，经过逆傅里叶变换就可以得到左侧的图像。

        同理，将通过的频率扩大，得到结果如下图所示，边界就更加明显了。

2.4.2卷积

        在图形学中，卷积(Convolution)实际上就是定义一个滤波器(滤波器也被称之为卷积核)，这个滤波器可以是一维数组也可以是二维数组，使用这个滤波器对原来的信号挨个进行处理，然后把处理好的结果写进一个与原数据相同大小的容器中，滤波的本质是将信号与滤波器在时域上进行卷积的操作。

        假设一个一维数组的信号(Signal)，然后定义一个滤波器(Filter)。这个滤波器也是一个一维数组，数组中的权重分别是1/4,1/2,1/4。如下图所示：

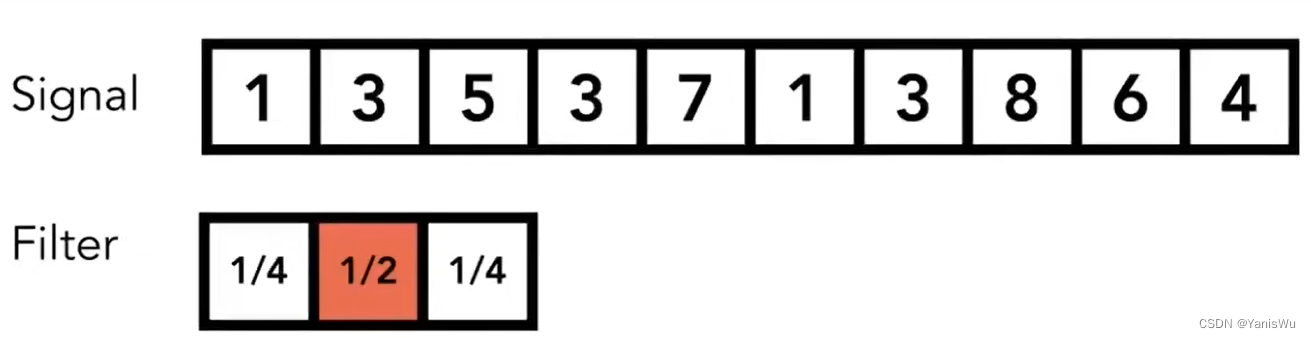
        用这个卷积核与原信号中卷积核覆盖的值做叉乘，将结果写入到原信号对应的位置，具体如下图。

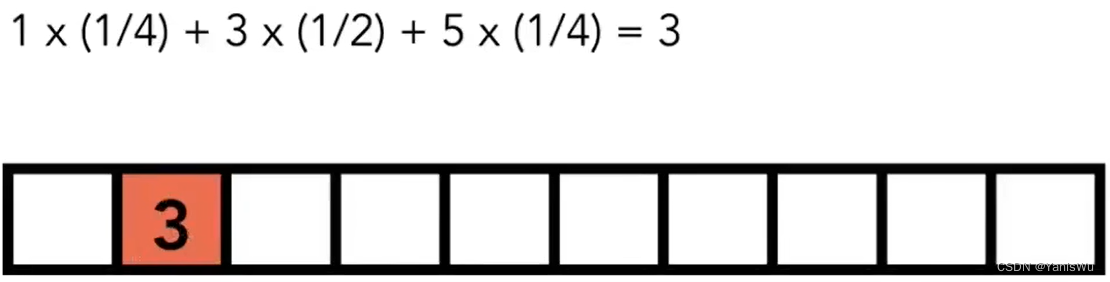
        接着卷积核向右移动一格，处理下一个信号，原信号的第三个元素。如下图所示：

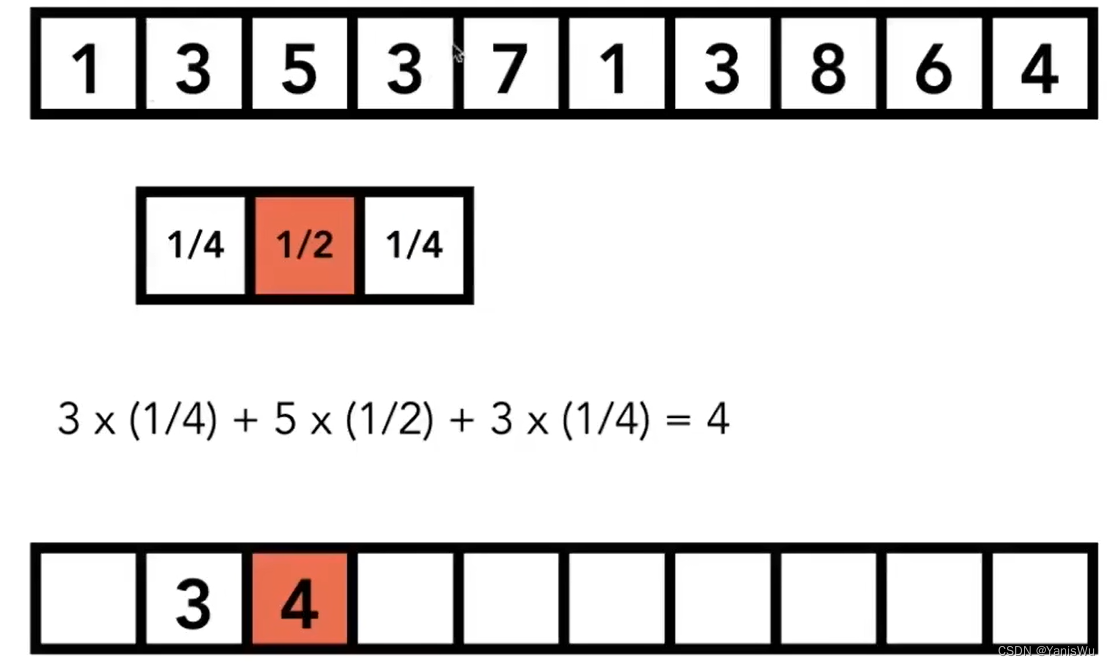
        依次处理完每一个信号得到的结果就是经过该卷积核卷积操作的结果。 综上，卷积就是在任何一个位置和它周围做一下平均。

卷积定律：

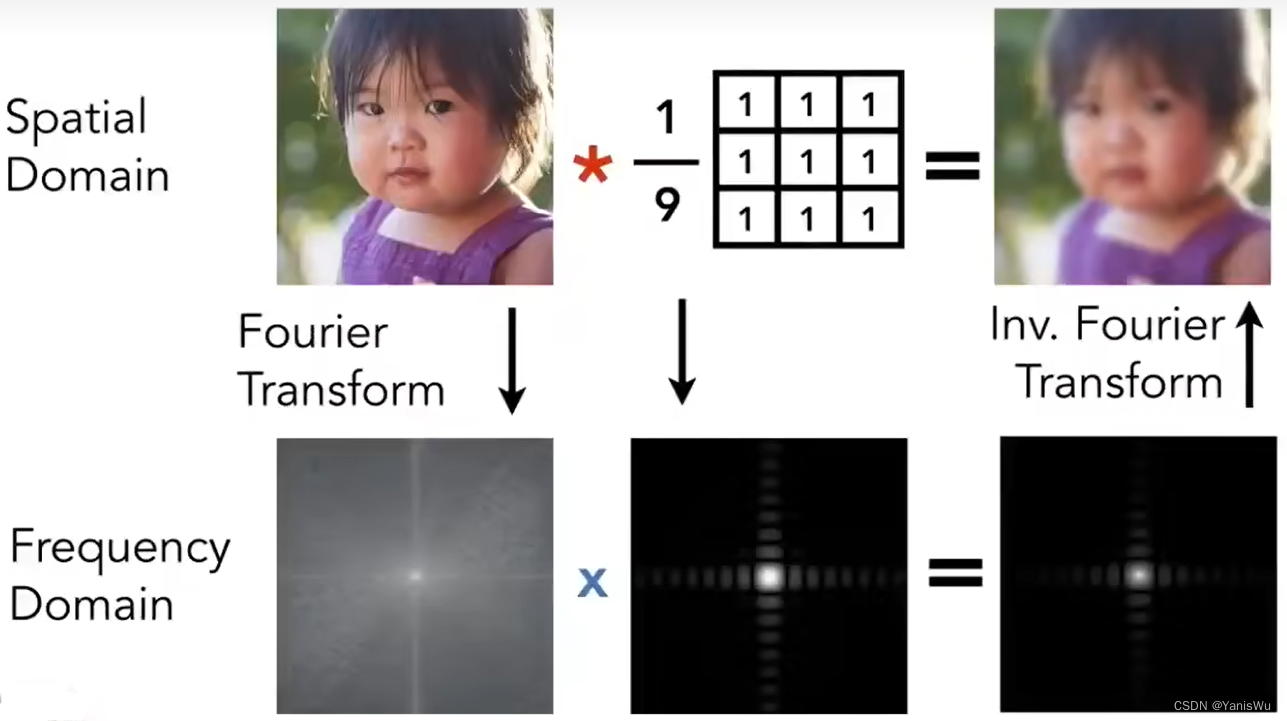
        上图中上半部分表示，一张图片进行使用3*3的一个卷积核进行卷积操作，求一下平均，得到的结果一张模糊的图片。同时如果对原始图片进行傅里叶变换，把图片从时域转换到频域，卷积核也经过傅里叶变换从时域转换到频域，这时把两个频域的结果相乘，然后进行逆傅里叶变换得到的结果与在时域上进行卷积操作的结果一样，这其实就是卷积定律的一部分内容：时域上的卷积相当于频域上的乘积。

        这里来看一下这个3*3的卷积核乘了个1/9，这是为了让卷积后的图像颜色与原本颜色不发生变化。在做卷积操作时会取原图像中的9个像素与卷积核中的元素分别相乘再相加，如果不乘以1/9，得到的结果是原来的9倍，会导致图像异常明亮，乘以1/9其实是对处理结果进行了一个归一化的操作。

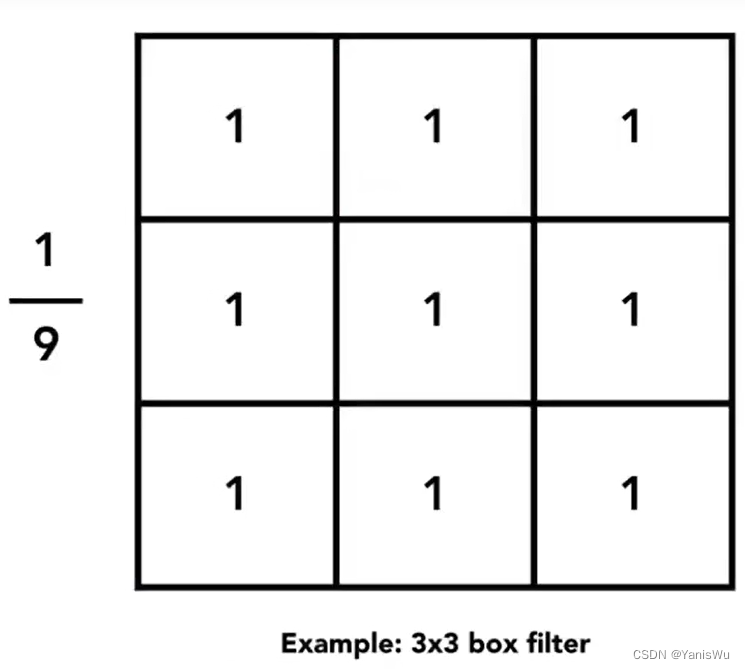
        卷积核经过傅里叶变换后，可以发现它大都是低频信号，所以卷积核可以认为是一个低通滤波器。

        下面举个例子，如下图所示，是一个卷积核从时域变换成频域的过程，如果变化卷积核时域的大小，频域会如何变换呢？

        通过上面的图片发现，卷积核在时域上变大，它在频域上反而变小了，也就是使用越大的卷积核经过卷积处理得到的图像会越模糊。可以这么理解，比如对一张图片进行模糊处理，使用一个3*3的卷积核进行模糊操作。然后再使用一个64*64的卷积核(时域变大)进行模糊操作，可想而知，周围取的像素越多进行平均处理，那肯定越模糊。

2.4.3采样与频域

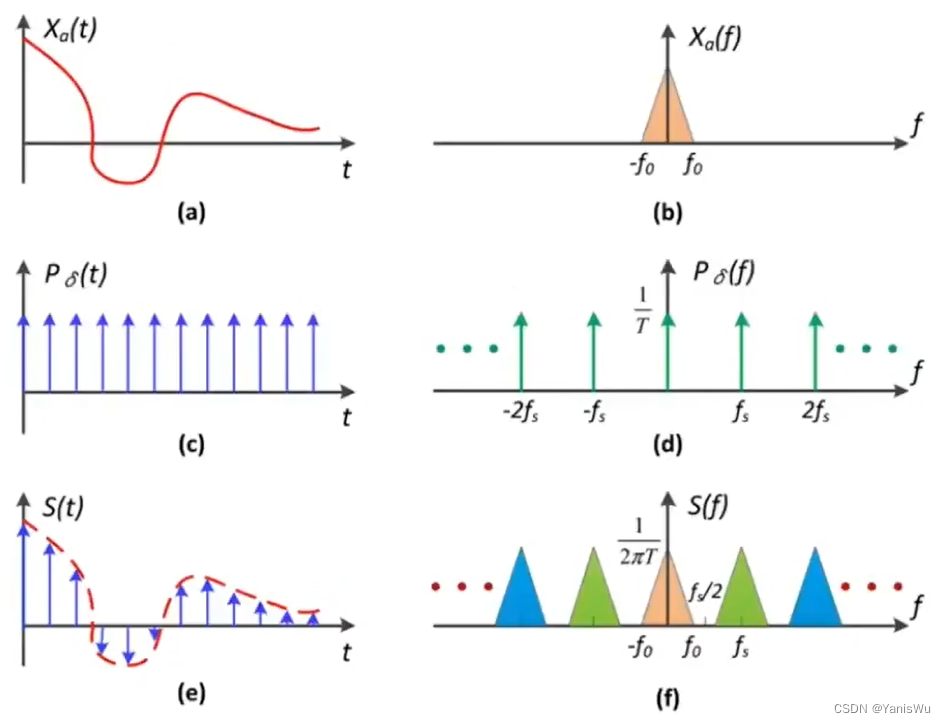
        如上图，假设a是一个连续的函数(信号)，经过傅里叶变换后在频域上的体现为b。然后要对a函数进行采样，需要把函数变成离散的点，只留下某些位置的值，就好像乘以另外一个函数c，c也称冲击函数，d是冲击函数在频域上的体现。而a和c乘出来的结构就是e函数，其实就是采样的信号。b和d的卷积为f，f又是e经过傅里叶变换的频域，所以得到另外一条卷积定律：时域上的乘积相当于频域上的卷积。

        通过上面的几幅图片可以发现，取样结果在频域上的体现就是把原本频域的信号进行重复，也可以认为采样就是在重复原始信号的频谱。这样就能明白为什么会产生走样现象了。

3.反走样方法

3.1走样的本质

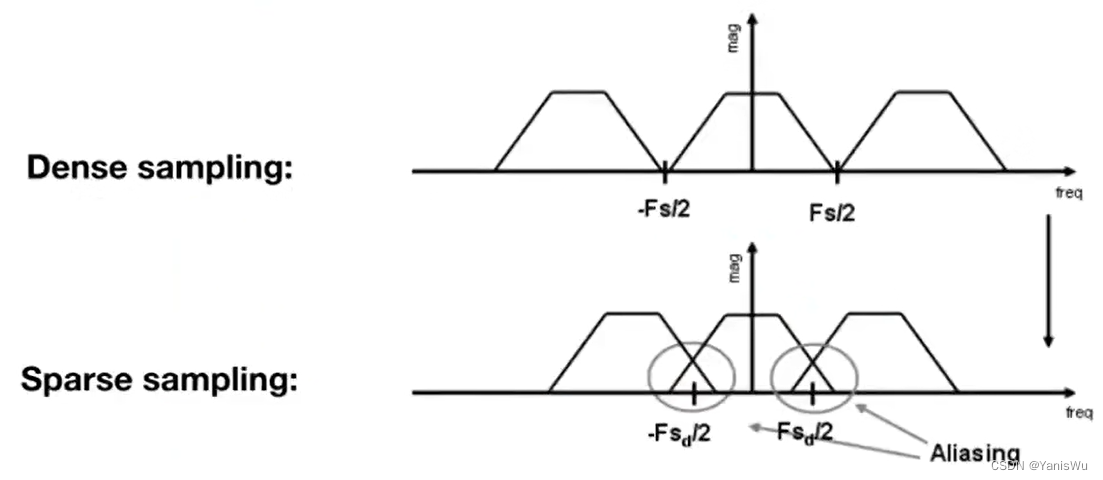
        根据上面已经知道采样是根据冲击函数的间隔(频率)在重复信号的频谱。上图的上半部分为函数的频谱，当采样频率小于频谱频率时，就会出现下半部分混叠的现象，这就是发生走样现象的本质。采样越稀疏(慢)，在频域上越密。

3.2反走样几种方法

        提高清晰度最直接的就是用更高的屏幕分辨率，但是这不是反走样要做的事情。在本章最开始的时候，通过在采样之前先对图像进行模糊处理，从而达到了反走样的效果。为什么这样做呢？可以看如下图所示：

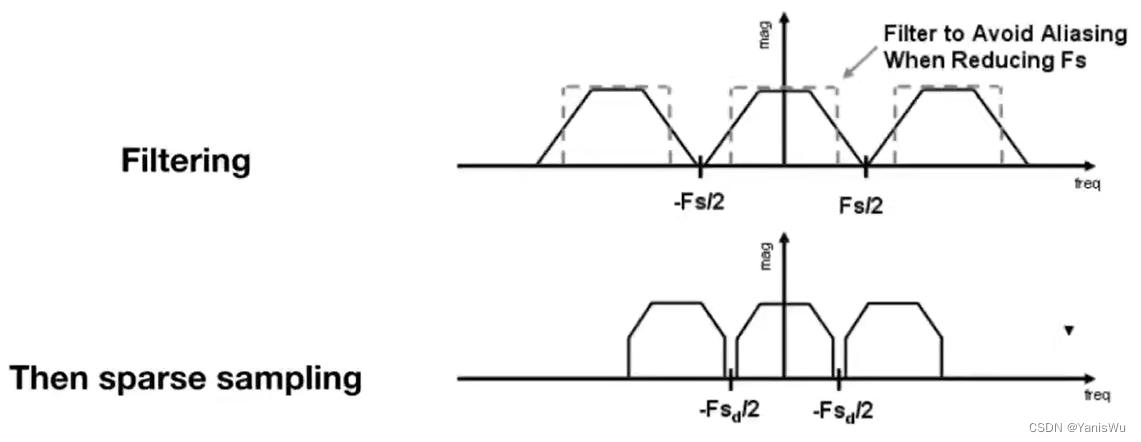
        通过之前的频率分析，模糊就是低通滤波，先把高频信息去除再做同样采样。会发现原本混叠的部分在采样前被过滤掉了，这样信号最大限度的保持了原有的样子，又保证不会发生混叠，进而达到反走样的目的。

        那么怎么让三角形变模糊呢？可以通过卷积操作，f(x,y)=inside(triangle,x,y)在像素区域内的平均值等于三角形所覆盖的像素面积。如下图所示。

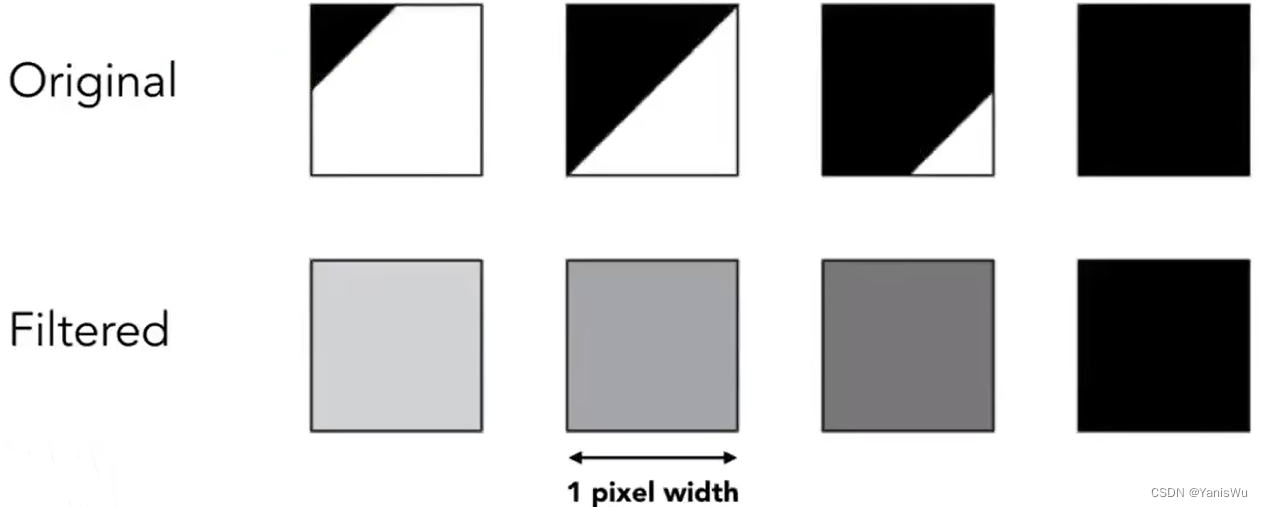
        但是这事说的容易，做的难，怎么将一个三角形在某一个像素里覆盖的区域算出来是一个难题。在实际中，有以下几种反走样的方法。

3.2.1多重采样 MSAA

        多重采样 MSAA(Multi Sampling Anti-Aliasing)是将一个像素划分为很多小的像素，同样每个小的像素也有各自的中心点。然后根据小像素的在三角形中的个数得到这个像素在三角形中的覆盖率，通过覆盖率可以算出这个像素对应的颜色。MSAA实际上解决的是对图形进行模糊操作的这个过程，他只是通过近似的一种方法进行模糊，只是增加了采样点并没有提高屏幕分辨率。如下图所示，是将一个像素分成4个小像素。缺点是增加了计算量。

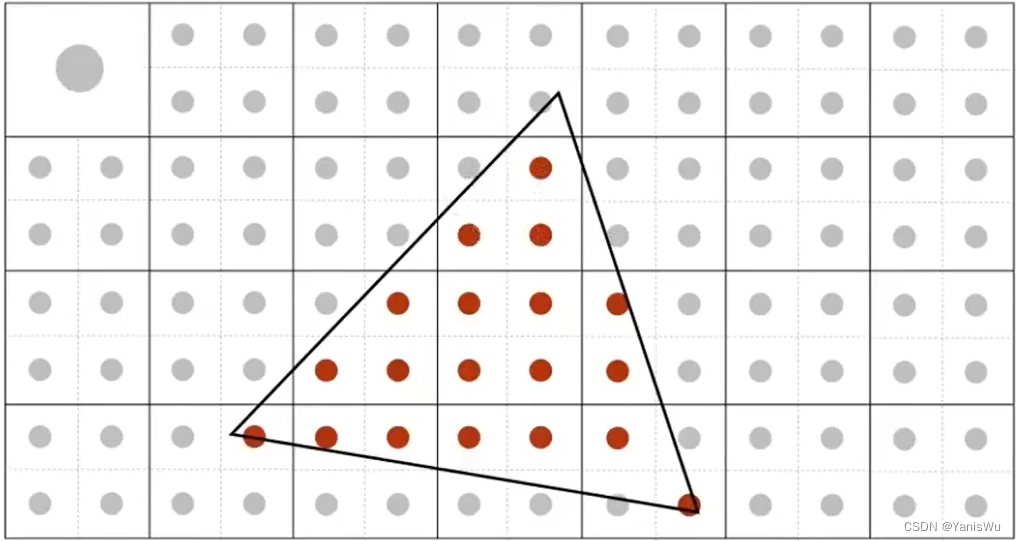
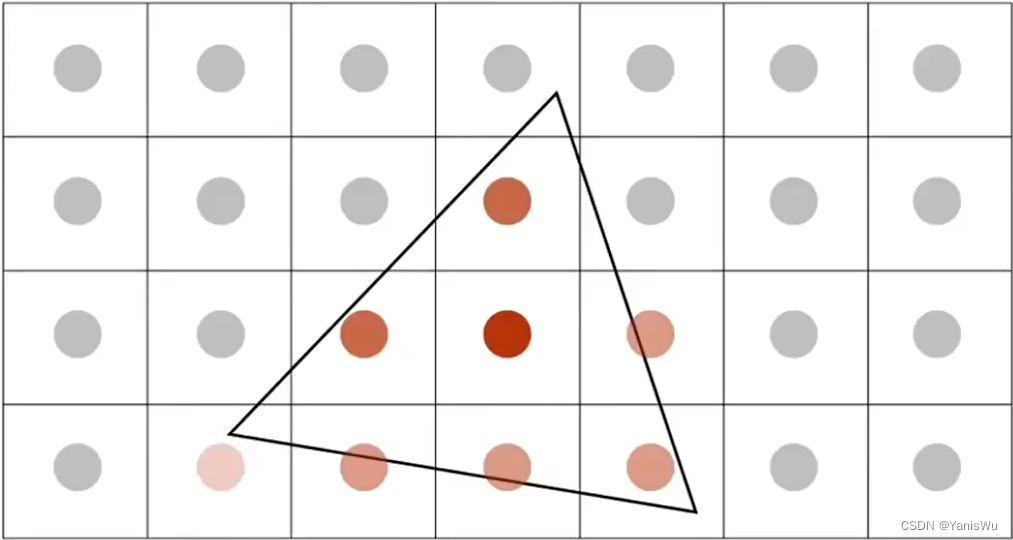
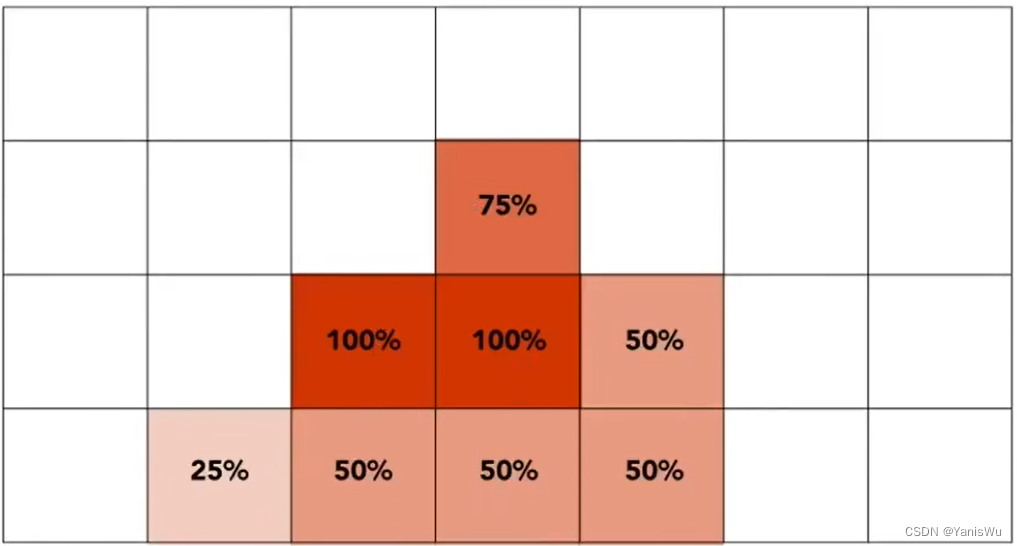
        注意：上图第三张图片中间左侧应该是75%，不是100%。

3.2.2快速近似抗锯齿 FXAA

       快速近似抗锯齿 FXAA(Fast Approximate Anti-Aliasing)，他是一种和采样无关，是图像层面的后期处理，处理过程是先找到三角形的边界，把有锯齿的边界替换为没有锯齿的边界，而且处理起来非常快。

3.2.3时间抗锯齿 TAA

        时间抗锯齿 TAA(Temporal Anti-Aliasing)，最大的特点就是非常快速，是将静态的图片在时间上进行采样，图像不做MSAA，相连两帧显示的图像是一样，但是可以用相邻两帧同一个像素上不同位置的点来感知是否在三角形内，计算的时候要考虑上一帧感知的结果要被应用进来，相当于是MSAA对应的样本分布在时间上，并且当前这帧没有任何额外的操作。

3.2.4深度学习超级采样 DLSS

        超分辨率(Super-resolution)就是将一张小分辨率拉大到大分辨率，正常来说会出现锯齿，通过深度学习可以猜测细节，并将细节补上去，就会得到一张高清的高分辨率图。与抗锯齿无关，是与MSAA一个相似的过程，都是解决样本不足的问题，虽然不是一回事，但是本质相同。那么这里就介绍一种使用是深度学习来做超采样的过程，就是深度学习超级采样 DLSS(Deep Learning Super Sampling)。