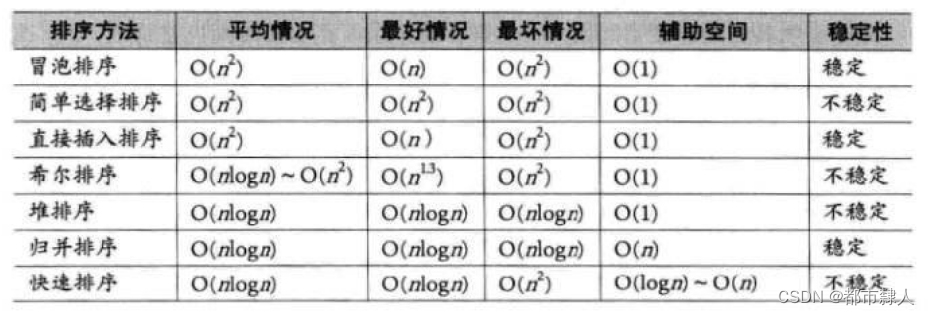
一、排序总结
性能指标:稳定性,时间复杂度,空间复杂度
排序算法的稳定性是指当排序的元素中存在相同的值时,排序算法能够保持它们原先的相对顺序。如果一个排序算法是稳定的,那么在排序后,相同值的元素在原始序列中的相对位置不会改变。这意味着如果两个元素A和B的值相同,并且在原始序列中A出现在B之前,那么在排序后A仍会出现在B之前。
稳定性对于一些特定的应用很重要,比如对于具有相同值但不同其他特性的元素进行排序时,我们希望保持它们的原始位置关系。例如,对于学生成绩相同但按照不同条件排序的情况,稳定性就显得尤为重要。因此,对于某些应用来说,稳定性是排序算法的一个重要性质。

二、比较排序
2.1 冒泡排序
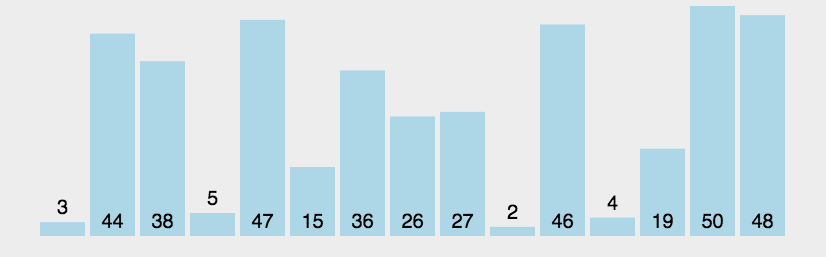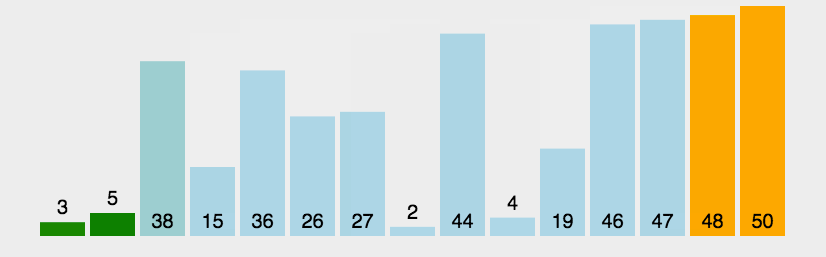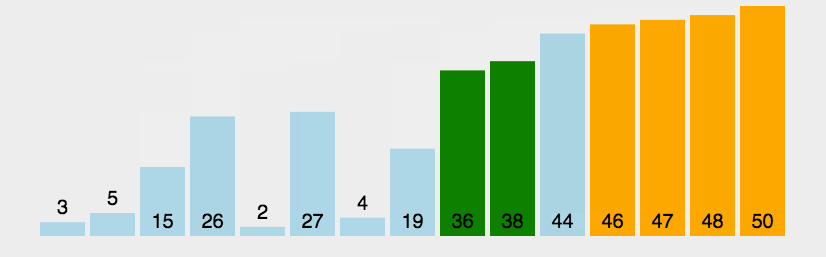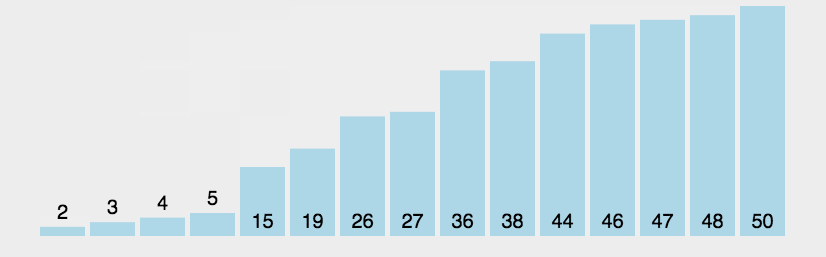
void Bubble_sort(int arr*, int size)
{
int j,i,tmp;
for (i = 0; i < size-1;i ++)
{
int count = 0;
for (j = 0; j < size-1 - i; j++)
{
if (arr[j] > arr[j+1]) //升序
{
tem = arr[j];
arr[j] = arr[j+1];
arr[j+1] = tmp;
count = 1;
}
}
if (count == 0) //如果没有交换位置,则说明已经排好序,直接退出循环
{
break;
}
}
2.2 简单选择排序
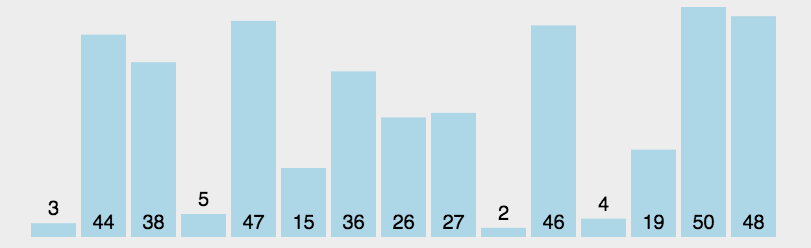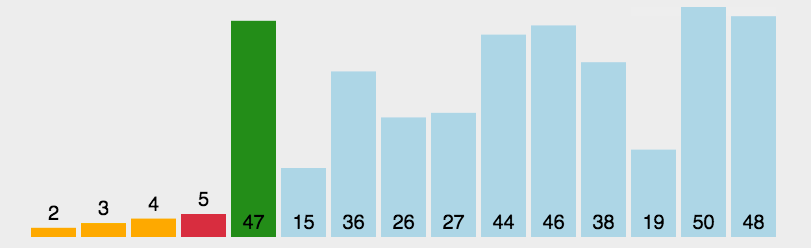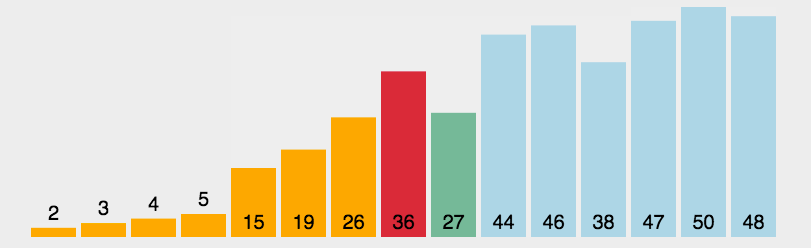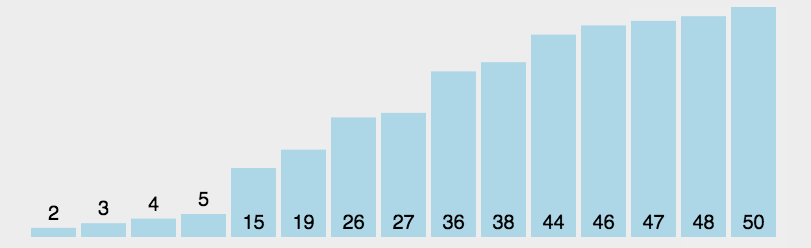
常见排序算法之选择排序-CSDN博客
2.3 直接插入排序
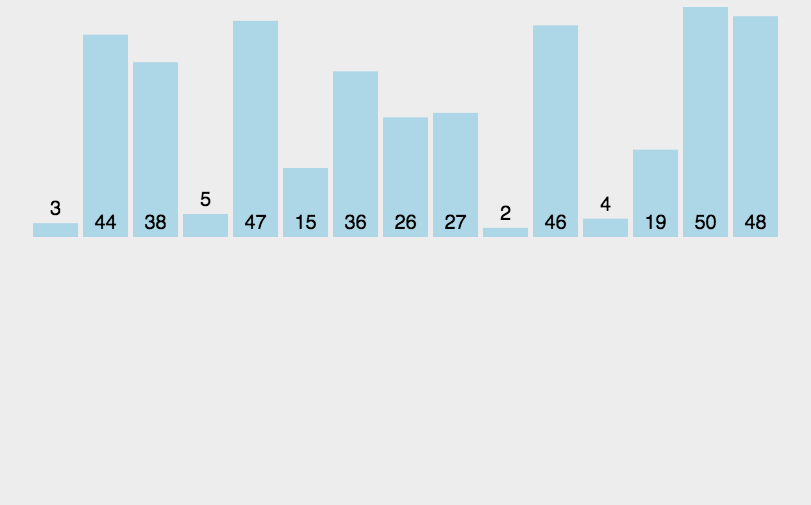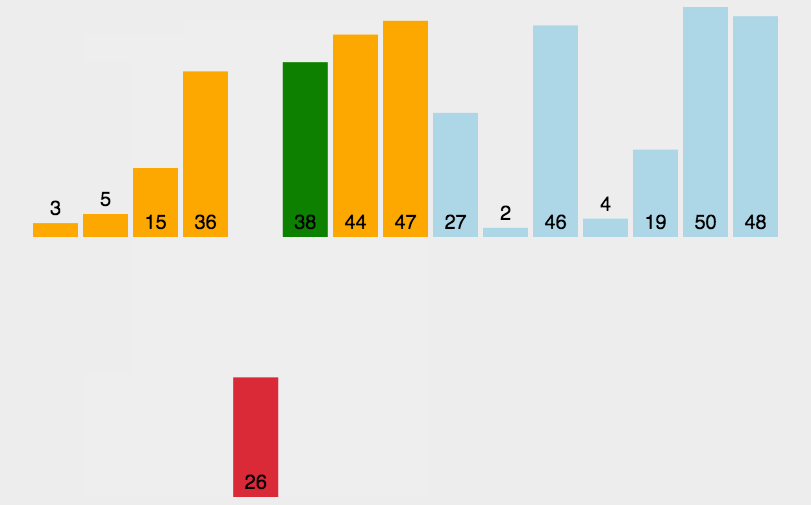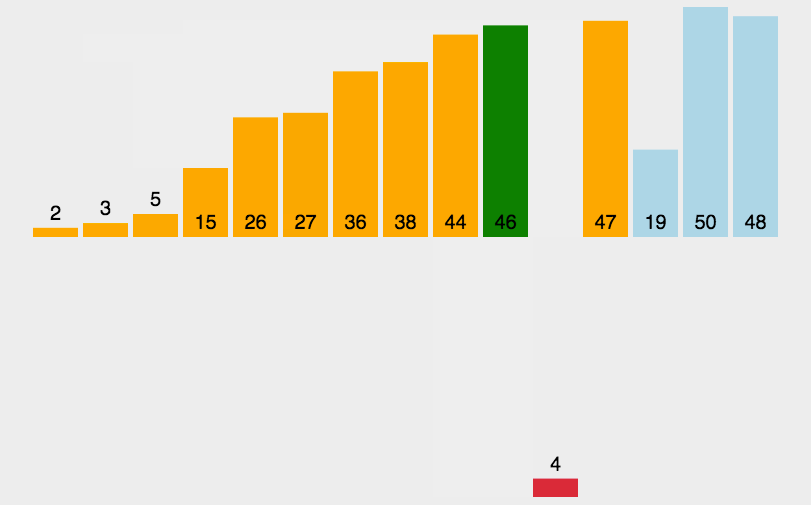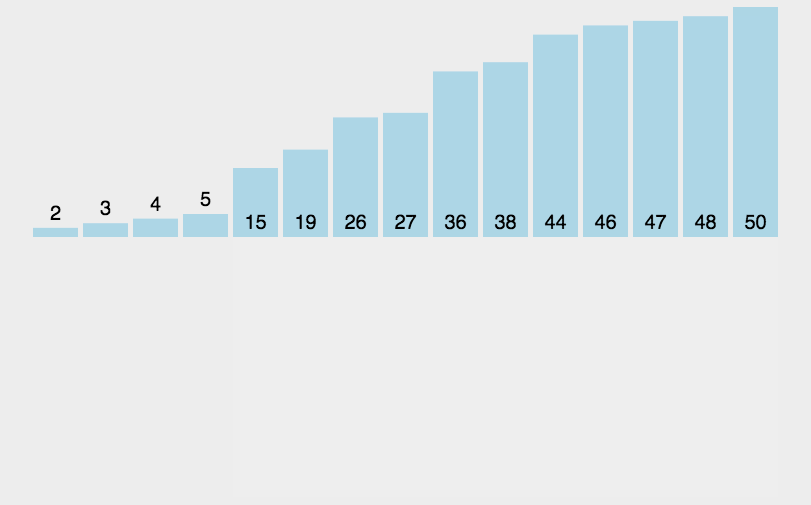
常见排序算法之插入排序_插入排序 csdn-CSDN博客
2.4 希尔排序
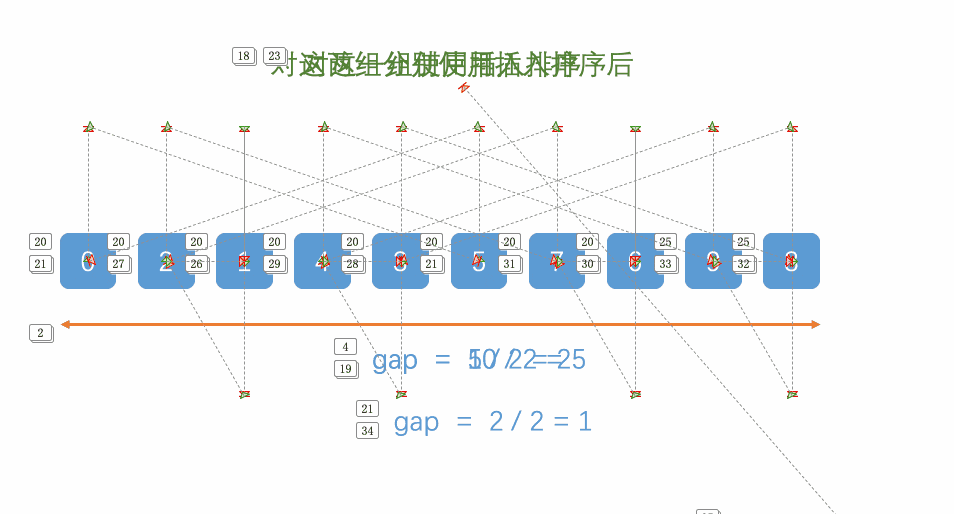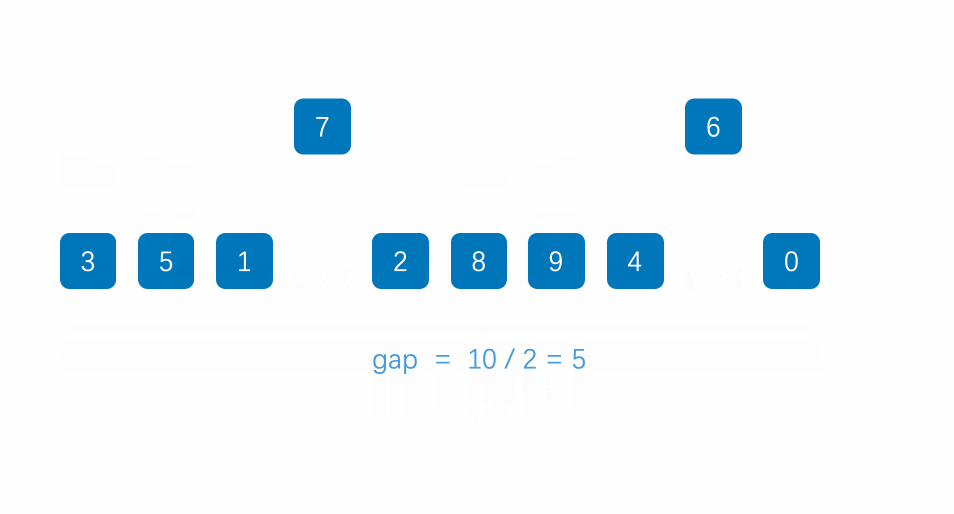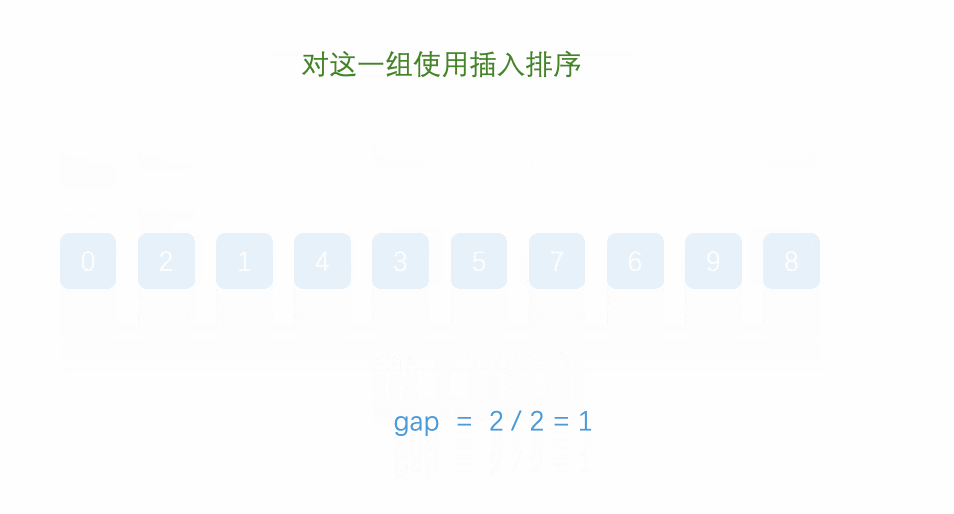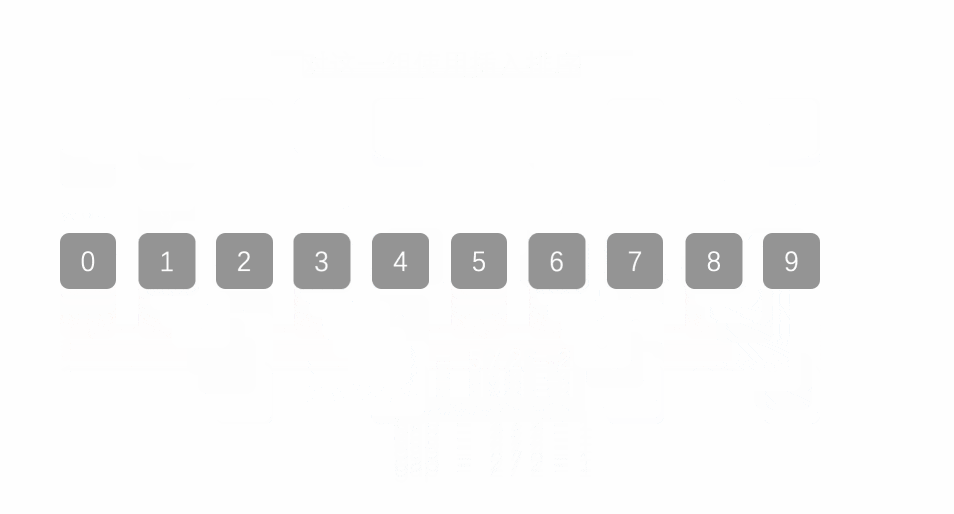
常见排序算法之插入排序_插入排序 csdn-CSDN博客
2.5 堆排序
堆排序详细理解-CSDN博客
2.6 归并排序
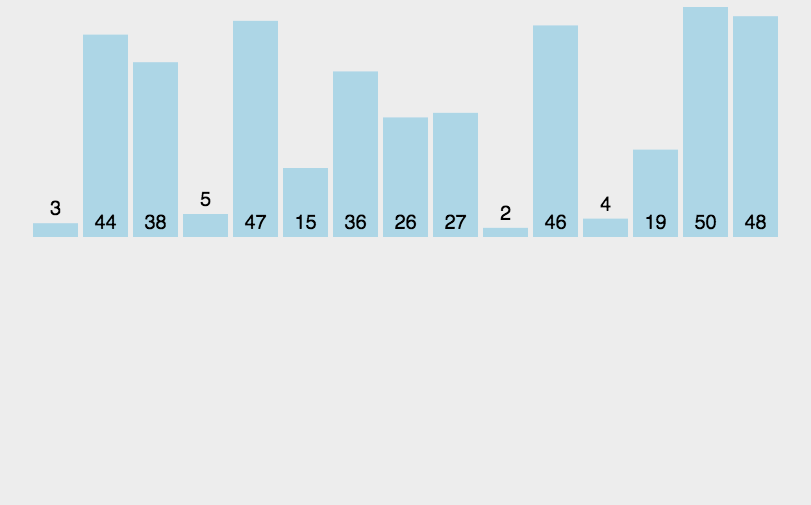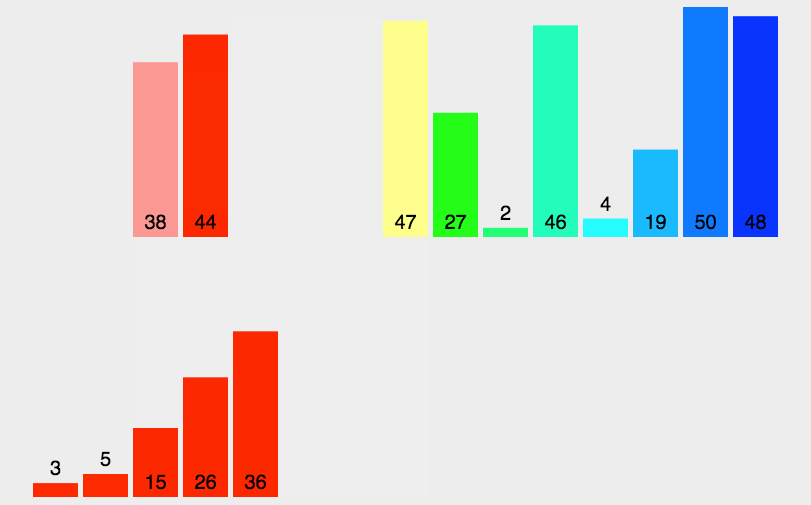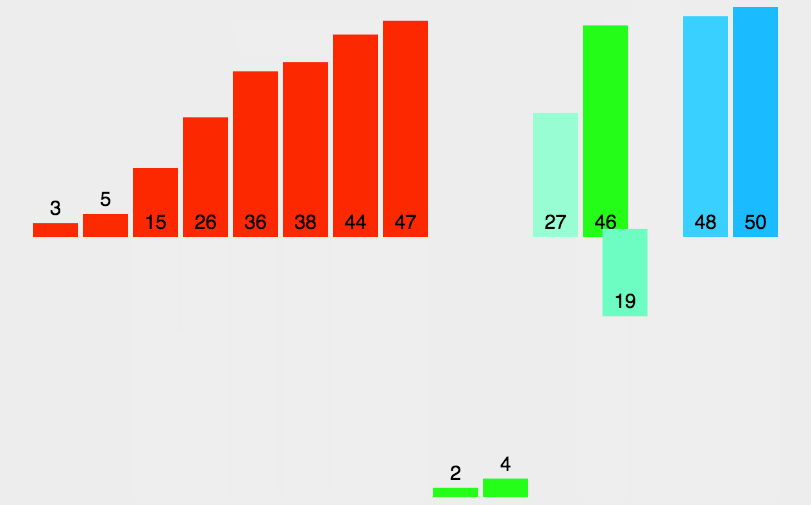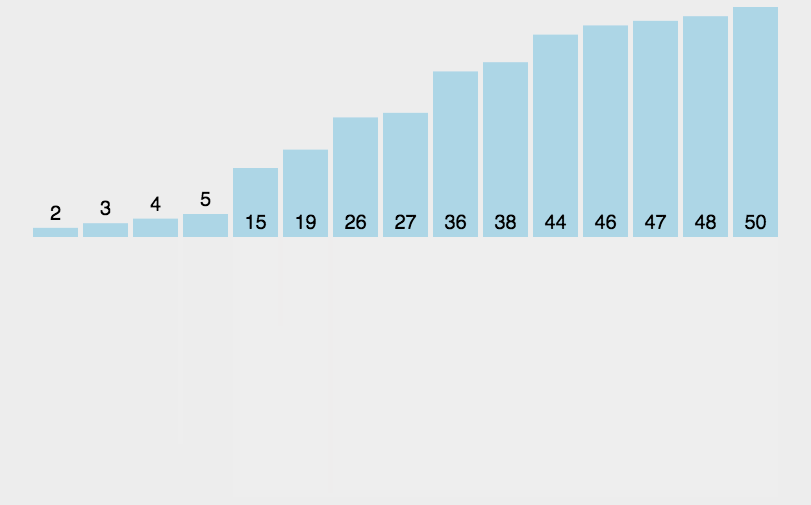
常见排序算法之归并排序-CSDN博客
2.7 快速排序
常见排序算法之快速排序-CSDN博客
三、非比较排序
3.1 桶排序
3.2 基数排序
基数排序详解-CSDN博客
基数排序的时间复杂度和空间复杂度也取决于待排序序列的长度和元素的范围。
时间复杂度:
在一般情况下,对于n个d位数,基数排序的时间复杂度为O(d*(n+k)),其中n是待排序序列的长度,k是每一位数字的范围。需要进行d轮排序,每轮排序的时间复杂度为O(n+k),因此总的时间复杂度可以表示为O(d*(n+k))。空间复杂度:
基数排序的空间复杂度取决于辅助空间的使用。在基数排序中,通常需要一个大小为n的辅助数组以及一个大小为k的桶数组,因此基数排序的空间复杂度为O(n+k)。
3.3 计数排序
非比较排序之计数排序-CSDN博客
计数排序是一种非比较排序算法,其时间和空间复杂度取决于待排序序列中元素的范围。
时间复杂度:
- 最好情况时间复杂度为O(n+k),其中n是待排序序列的长度,k是待排序序列中的最大值和最小值的差值加上1。在最好情况下,计数排序仅需要遍历一遍待排序序列,并且需要遍历k个计数数组。
- 最坏情况时间复杂度亦为O(n+k)。
- 平均情况时间复杂度也是O(n+k)。
空间复杂度:
- 空间复杂度为O(k),其中k是待排序序列中的最大值和最小值的差值加上1。计数排序需要一个大小为k的辅助数组来存储计数的中间结果。