主成分分析(Principal components analysis,PCA)是一种线性降维方法。它利用正交变换对一系列可能相关的变量的观测值进行线性变换,从而投影为一系列线性不相关变量的值,这些不相关变量称为主成分(Principal Components)。PCA是一种对数据进行简化分析的技术,这种方法可以有效地找出数据中最“主要”的元素和结构,去除噪音和冗余,将原有的复杂数据降维,揭示隐藏在复杂数据背后的简单结构。
举个通俗易懂的例子:以学习成绩为例,每个同学有多门考试成绩(即分数),例如语文75、数学78、英语86等等。如果有10门课程,那么每个同学的成绩就有10个维度,10个维度对于我们了解这个同学的成绩来说,有点复杂。这时,我们可以用成绩好和成绩不好来表征这个同学的成绩,这就是“降维”。
“PCA降维”的目的:
1)去冗余
例如微积分成绩和概率论的成绩一般是强相关,这样就可以将10个维度去掉1个维度)
2)发现异常值
例如某同学由于疫情被隔离了几天,缺了几门课的成绩,那么降维后就可以在2D图上找到该同学所代表的点,后续分析时可以考虑踢掉
3)保留原始信息
降维后新的主成分能够解释原数据,如果降维后可解释性降低,那么就不是好的降维
大多数情况下,降维是为聚类、分类服务的。降维后,我们就可以研究同学们的成绩情况,寻找隐藏在成绩背后的信息,例如,有几个学生成绩都很好,那么“他们住在同一个宿舍”就有可能是潜在变量。
降维的方法有很多种,常见的包括线性降维(PCA、PLS),非线性降维(UMAP,tSNE)等。降维后一般会进行2D,或者3D图的绘制,其中2D图最常见也最容易理解。一般我们绘制individuals散点图,也就是将看得见,摸得着的样本点(例如常规RNAseq结果中的15个样品或者单细胞测序中的成千上万个细胞等)绘制在X/Y轴坐标系中。
对主成分分析(Principal components analysis,PCA)有了简单地解后,我们就可以用微生信网站进行发表级PCA绘图了。
1,打开绘图页面
微生信-在线绘制主成分分析图(Principal component analysis,PCA)
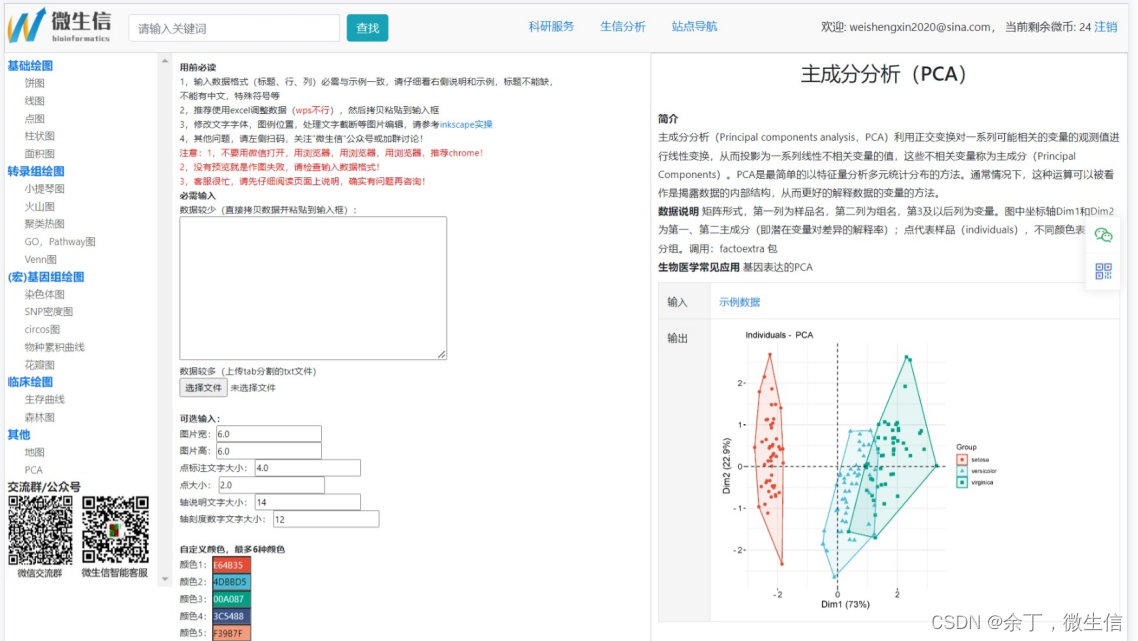
2,下载示例数据
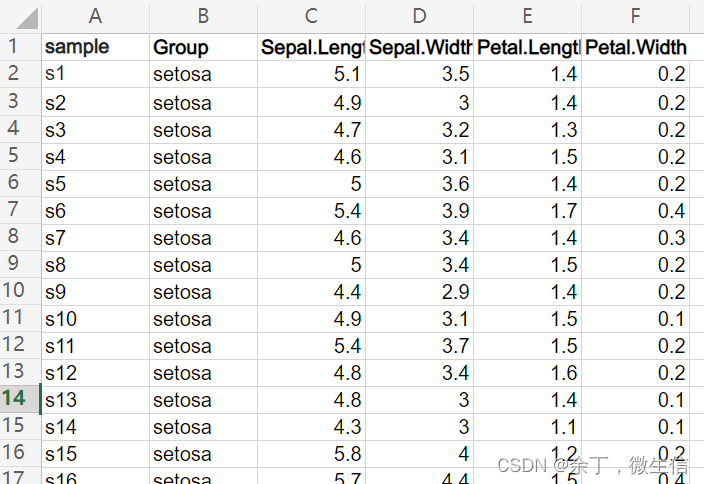
这是最经典的鸾(音:yuān)尾花数据,该数据测量了三种鸢尾花(B列:Setosa鸢尾花、Versicolour鸢尾花和Virginica鸢尾花)的4个属性数据(C:花萼长度、D:花萼宽度、E:花瓣长度、F:花瓣宽度),每种花收集了50条样本记录,共计150条(A列:s1-s150)。

3,拷贝并粘贴示例数据

4,修改参数,并提交

图片大小颜色形状以及标注字体大小等都可以个性化定制,可满足不同的绘图需求。
5,提交出图

该图展示了150个样品在第一主成分(73%)和第二主成分(22.39%)的散点图,百分比表示可解释程度,即第一主成分可以解释数据属性的73%。将4维空间降维为2维空间后,可以较明显地看出这150个样本呈现为3群。
该模块调用了FactoMineR、factoextra等R包。
没有预览就是没有出图,这时请参考示例数据,检查输入数据格式!
遇到文字截断,需要修改字体、调整字体大小等,使用inkscape软件进行操作。
微生信助力高分文章,用户185000,谷歌学术3600篇