作为一种非常有潜力的代替MLP的模型,KAN最终获得了学术界极大的关注。在我昨天的博客里,解读了最近的热门模型KAN:
论文阅读KAN: Kolmogorov–Arnold Networks-CSDN博客
KAN的原文作者提到了很多不足。本文算是对其中两个现有不足的回应,也就是:1)KAN不仅只能用于特定结构和深度,2)KAN不仅能用于小规模AI+Science任务,还可以用于更大规模或更复杂的任务。
本文将KAN融入了U-Net网络结构中,并运用在医学图像分割任务上。
1,U-KAN架构
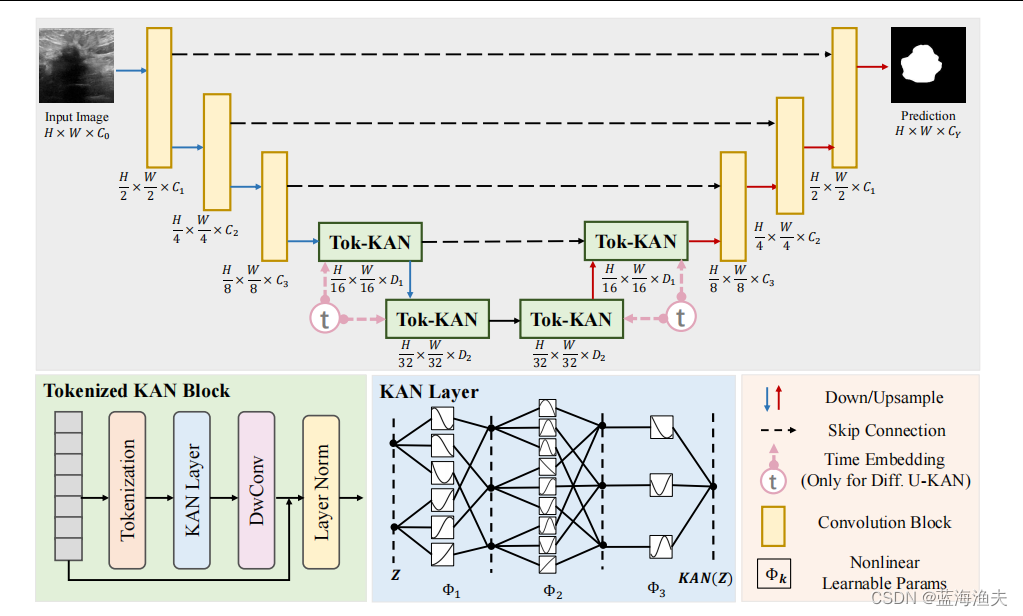
整体结构如图,是个U-Net经典的对称编解码器结构。编解码器都有卷积部分和token化KAN模块部分组成。卷积部分如U-Net一样,不赘述。
Token化的KAN模块:
1)token化:首先对特征进行重塑,得到一系列扁平化的二维patch。接着进行线性投影,线性投影是通过一个核大小为3的卷积层实现的。卷积层足以编码位置信息,并且其性能实际上优于标准的位置编码技术。
2)KAN块:在获取到token之后,我们将它们传入一系列的KAN层(N=3)。在每个KAN层之后,特征会通过一个高效的深度卷积层(DwConv)、一个批量归一化层(BN)和一个ReLU激活函数。此外,还是用了残差连接。
2,消融实验
1)KAN层层数影响

2)KAN层换成MLP的话,结果会下降(在我看来本文最重要的结论也就是这个)

3)模型规模的影响

3,与SOTA对比

4,本文的缺陷与不足
本文在我看来有两个主要不足:
1)训练难度:KAN至关重要的训练难度问题没有提及。将KAN结构嵌入U-Net是否会导致训练变得不稳定或难以收敛呢?训练速度会慢多少呢?
2)实验对比不充分,结果可能不SOTA:
本文的对比实验,完全没有对比基于Transformer的图像分割模型,对比的几个模型要么是纯卷积模型,要么是卷积+MLP模型。那么我们是否可以认为U-KAN的结果逊于主流的Transformer分割模型?
5总结
在我看来,虽然本文模型大概率并不SOTA,但是也不是非要SOTA的模型和实验才有价值。
本文的价值在于验证了KAN可以用于更广泛的数据集,并且在更多场景下展现了超越和取代MLP的潜力。