微♥关注“电击小子程高兴的MATLAB小屋”获得资料
一、理论基础
1、路径规划算法
路径规划算法是指在有障碍物的工作环境中寻找一条从起点到终点、无碰撞地绕过所有障碍物的运动路径。路径规划算法较多,大体上可分为全局路径规划算法和局部路径规划算法两大类。其中,全局路径规划算法包括位形空间法、广义锥方法、顶点图像法、栅格划归法;局部路径规划算法主要有人工势场法等。
2、MAKLINK图论理论
MAKLINK图论可以建立二维路径规划的空间模型,其通过生成大量的MAKLINK线构造二维路径规划可行空间。MAKLINK线定义为两个障碍物之间不与障碍物相交的顶点之间的连线,以及障碍物顶点与边界相交的连线。典型MAKLINK图形如图1所示。
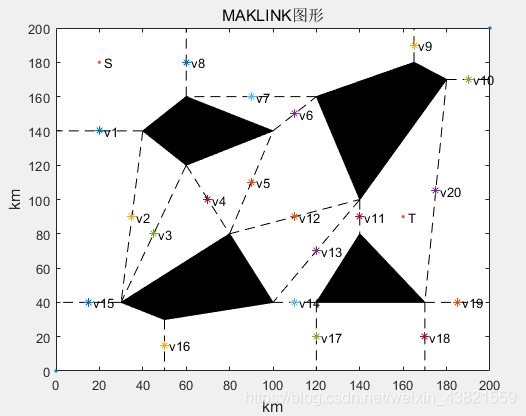
图1 MAKLINK图形
在MAKLINK图上存在I条自由连接线,连接线的中点依次为1,V2,连接所有MAKLINK线的中点加上始点S和终点工构成用于初始路径规划的无向网络图,如图2所示。
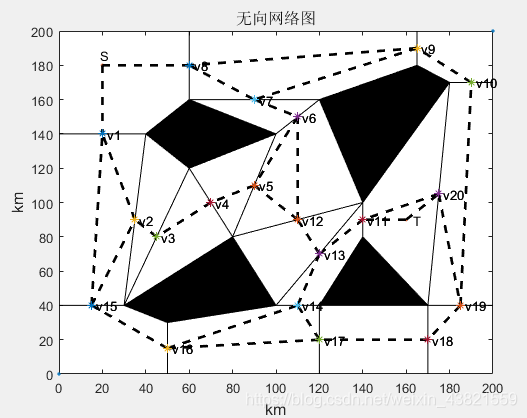
图2 无向网络图
3、蚁群算法
请参考这里
4、dijkstra算法
dijkstra算法是典型的单源最短路径算法,用于计算非负权值图中一个节点到其他所有节点的最短路径,其基本思想是把带权图中所有节点分为两组,第1组包括已确定最短路径的节点,第2组为未确定最短路径的节点。按最短路径长度递增的顺序逐个把第2组的节点加入第1组中,直到从源点出发可达的所有节点都包含在第1组中。
dijkstra算法流程如下:
(1)初始化存放未确定最短路径的节点集合V VV和已确定最短路径的节点集合S SS,利用带权图的邻接矩阵arcs初始化源点到其他节点最短路径长度D DD,如果源点到其他节点有连接弧,对应的值为连接弧的权值,否则对应的值取为极大值。
(2)选择D DD中的最小值D DD[i ii],D DD[i ii]是源点到点i ii的最短路径长度,把点i ii从集合V VV中取出并放入集合S SS中。
(3)根据节点i ii修改更新数组D DD中源点到集合V VV中所有节点k kk对应的路径长度值。
(4)重复步骤(2)和步骤(3)的操作,直至找出源点到所有节点的最短路径为止。
二、案例背景
1、问题描述
采用蚁群算法在200×200的二维空间中寻找一条从起点S SS到终点T TT的最优路径,该二维空间中存在4个障碍物,障碍物1的4个顶点的坐标分别为(40 140;60 160;100 140;60 120),障碍物2的4个顶点分别为(50 30;30 40;80 80;100 40),障碍物3的4个顶点分别为(120 160;140 100;180 170;165 180),障碍物4的3个顶点分别为(120 40;170 40;140 80),其中点S SS为起点,起点坐标为(20,180);点T TT为终点,终点坐标为(160,90)。二维规划空间如图3所示。
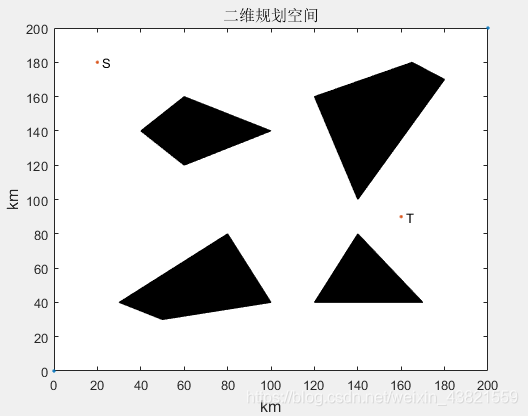
2、算法流程
算法流程如图4所示。其中,空间模型建立采用MAKLINK图论算法建立路径规划的二维空间,初始路径规划利用dijkstra算法规划出一条从起点到终点的初始路径,初始化算法参数,信息素更新采用根据蚂蚁搜索到的路径的长短优劣更新节点的信息素。
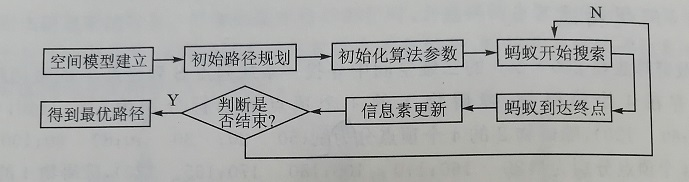
三、MATLAB程序
根据蚁群算法原理,在MATLAB软件中编程实现基于蚁群算法的二维路径规划算法,算法分为两步:第一步使用dijkstra算法生成初始次优路径;第二步在初始路径的基础上,使用蚁群算法生成全局最优路径。
1、dijkstra算法
采用dijkstra算法规划初始路径,其算法思想是先计算点点之间的距离,然后依次计算各点到出发点的最短距离,程序如下:
function path = DijkstraPlan(position,sign) %% 基于Dijkstra算法的路径规划算法 % position input 节点位置 % sign input 节点间是否可达 % path output 规划路径 %% 计算路径距离 cost = ones(size(sign))*10000; [n, m] = size(sign); for i = 1:n for j = 1:m if sign(i, j) == 1 cost(i, j) = sqrt(sum((position(i, :)-position(j, :)).^2)); end end end %% 路径开始点 dist = cost(1, :); % 节点间路径长度 s = zeros(size(dist)); % 节点经过标志 s(1) = 1; dist(1) = 0; path = zeros(size(dist)); % 依次经过的节点 path(1, :) = 1; %% 循环寻找路径点 for num = 2:n % 选择路径长度最小点 mindist = 10000; for i = 1:length(dist) if s(i) == 0 if dist(i)< mindist mindist = dist(i); u = i; end end end % 更新点点间路径 s(u) = 1; for w = 1:length(dist) if s(i) == 0 if dist(u)+cost(u,w) < dist(w) dist(w) = dist(u)+cost(u,w); path(w) = u; end end end end
2、蚁群算法搜索
在初始路径的基础上,采用蚁群算法搜索最优路径,程序如下:
%% 蚁群算法参数初始化 pathCount = length(path)-2; % 经过线段数量 pheCacuPara = 2; % 启发值重要程度因子 pheThres = 0.8; % 信息素选择阈值 pheUpPara = [0.1 0.0003]; % 信息素更新参数 qfz = zeros(pathCount, 10); % 启发值 phePara = ones(pathCount, 10)*pheUpPara(2); % 信息素 qfzPara1 = ones(10,1)*0.5; % 启发信息参数1 qfzPara2 = 1.1; % 启发信息参数2 m=10; % 蚂蚁数量 NC=500; % 循环次数 pathk = zeros(pathCount, m); % 搜索结果记录 shortestpath = zeros(1,NC); % 进化过程记录 shortestroute = zeros(NC, 2*pathCount); % 每一代的最短路径 %% 初始最短路径 dijpathlen = 0; vv = zeros(22, 2); vv(1, :) = S; vv(22, :) = T; vv(2:21, :) = v; for i=1:pathCount-1 dijpathlen = dijpathlen +sqrt(sum((vv(path(i), :)-vv(path(i+1), :)).^2)); % dijpathlen = dijpathlen + sqrt((vv(path(i),1)-vv(path(i+1),1))^2+(vv(path(i),2)-vv(path(i+1),2))^2); end LL = dijpathlen; %% 经过的链接线 lines = zeros(pathCount, 4); for i = 1:pathCount lines(i, 1:2) = B(L(path(i+1)-1, 1), :); lines(i, 3:4) = B(L(path(i+1)-1, 2), :); end %% 循环搜索 for num = 1:NC %% 蚂蚁迭代寻优一次 for i = 1:pathCount for k = 1:m q = rand(); qfz(i, :) = (qfzPara2-abs((1:10)'/10-qfzPara1))/qfzPara2; % 启发信息 if q <= pheThres % 选择信息素最大值 arg = phePara(i, :).*(qfz(i, :).^pheCacuPara); j = find(arg == max(arg)); pathk(i, k) = j(1); else % 轮盘赌选择 arg = phePara(i, :).*(qfz(i, :).^pheCacuPara); sumarg = sum(arg); qq = (q-pheThres)/(1-pheThres); qtemp = 0; j = 1; while qtemp < qq qtemp = qtemp + (phePara(i, j)*(qfz(i, j)^pheCacuPara))/sumarg; j = j+1; end j = j-1; pathk(i, k) = j(1); end % 实时信息素更新 phePara(i, j) = (1-pheUpPara(1))*phePara(i, j)+pheUpPara(1)*pheUpPara(2); end end %% 计算路径长度 len = zeros(1, k); for k = 1:m Pstart = S; Pend = lines(1, 1:2) + (lines(1, 3:4)-lines(1, 1:2))*pathk(1, k)/10; for l = 1:pathCount len(1, k) = len(1, k)+sqrt(sum((Pend-Pstart).^2)); Pstart = Pend; ant_route(k, 2*l-1:2*l)=Pstart; if l < pathCount Pend = lines(l+1, 1:2) + (lines(l+1, 3:4)-lines(l+1, 1:2))*pathk(l+1, k)/10; end end Pend = T; len(1, k) = len(1, k)+sqrt(sum((Pend-Pstart).^2)); end %% 更新信息素 % 寻找最短路径 minlen = min(len); minant = find(len == minlen); minant = minant(1); shortestroute(num, :) = ant_route(minant, :); % 更新全局最短路径 if minlen < LL LL = minlen; LL_route = shortestroute(num, :); end % 路径信息素更新 for i = 1:pathCount phePara(i, pathk(i, minant)) = (1-pheUpPara(1))* phePara(i, pathk(i, minant))+pheUpPara(1)*(1/minlen); end shortestpath(num) = LL; end
3、结果分析
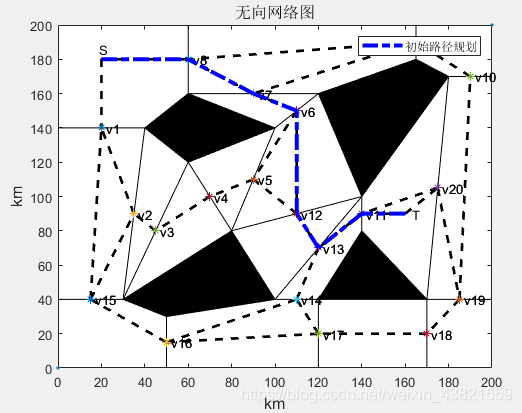
在无向网络图的基础上采用dijkstra算法规划初始路径,初始路径规划结果如图5所示。
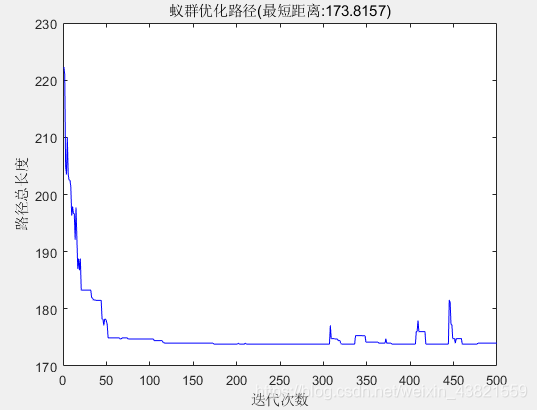
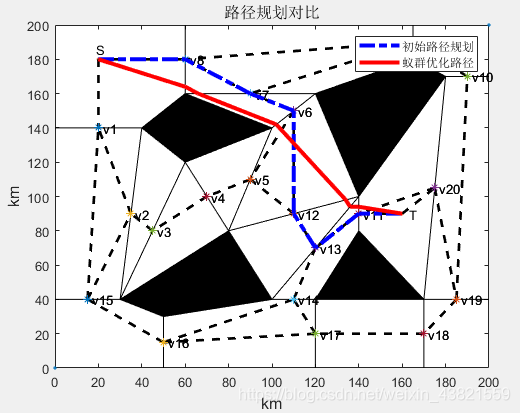
在初始路径规划的基础上采用蚁群算法进行详细路径规划。根据初始路径规划结果判断路径经过的链路为v8→v7→v6→v12→v13→v11,每条链路均离散化为10个小路段,蚂蚁个数为10,个体长度为6,算法进化次数共500次,迭代过程中路径总长度变化及规划出的路径如图6和图7所示。
Command Window中结果显示为:
初始路径:S->v8->v7->v6->v12->v13->v11->T 路径距离:229.0611 最短路径坐标:S->(60,164)->(66,160)->(102,142)->(134,98)->(136,94)->(140,94)->T 最短距离:173.8157