星网络 StarNet: Rewrite the Stars

论文题目：Rewrite the Stars

论文链接：http://arxiv.org/abs/2403.19967

代码链接：https://github.com/ma-xu/Rewrite-the-Stars

一、摘要

揭示星操作将输入映射到高维、非线性特征空间的能力——类似于核技巧——而无需扩展网络。提出了StarNet，一个简单而强大的原型，展示了在紧凑网络结构和高效预算下出色的性能和低延迟。重新书写和重新构造星操作可以生成一个包含大约 $(\frac{d}{\sqrt{2}})^2$ 个线性独立维度的新特征空间。
在这里插入图片描述

附录中有些图笔者认为比较具有参考意义，因此将其放于相关章节处。

文章目录

- 一、摘要
- 二、创新点
- 三、原理
- - 1、背景介绍
  - 2、Star Operation in One layer
  - 3、Generalized to multiple layers
  - 4、Special Cases
  - 5、Empirical Study
  - - Empirical superiority of star operation
    - Decision Boundary comparison
  - 6、Open Discussions & Broader Impacts
  - - I. 激活函数是否真的不可或缺？
    - II. 星操作如何与自注意力和矩阵乘法相关？
    - III. 如何优化隐式高维空间中的系数分布？
- 四、实验Proof-of-Concept: StarNet
- - - StarNet Architecture
    - Experimental Results
    - More Ablation studies
  - 五、总结

二、创新点

揭示了星操作具有将特征投影到一个极高维隐式特征空间的能力，类似于多项式核函数。
提出了一个概念验证模型StarNet。StarNet在无需复杂设计或精心选择的超参数的情况下取得了令人满意的性能，超越了许多高效设计。

三、原理

1、背景介绍

通过逐元素相乘融合不同的子空间特征。为了简便起见，文中将这种范式称为“星操作”（因为逐元素相乘符号类似于星号）。

在这里插入图片描述

如图1左侧所示。通过在一个干扰层后面堆叠多个演示块，构建了一个名为 DemoNet的简单模型。在保持其他因素不变的情况下，观察到逐元素相乘（星操作）在性能上始终优于求和，如图1右侧所示。

星操作类似于核函数，对跨不同通道的特征进行成对乘法，特别是多项式核函数。当星操作被纳入神经网络并堆叠多个层时，每一层都会导致隐式维度复杂性的指数增长。仅仅通过几层，星操作就能在一个紧凑的特征空间内实现几乎无限的维度。

在这里插入图片描述

图2中展示的简单可视化实验进一步说明了星操作与多项式核函数之间的联系。

2、Star Operation in One layer

在单层神经网络中，星号操作通常写为 $(W^{T}_{1} X + B_{1}) ∗ (W^{T}_{2} X + B_{2})$ ，表示通过逐元素乘法融合两个线性变换特征。写成矩阵的形式为 $(W^{T}_{1} X) ∗ (W^{T}_{2} X)$ ，其中 $W = [W, B]^{T}, X = [X, 1]^{T}$ 。

下面以一个输出通道转换和一个单元素输入场景为例，假设 $w_{1}, w_{2}. x \in R^{(d+1) \times 1}$ ，其中 $d$ 是输入通道数，扩展到多个输出通道 $W_{1}, W_{2} \in R^{(d+1) \times (d'+1)}$ ，并处理多个特征元素，其中 $\in R^{d+1} \times n$

一般地，星操作可以写为：
在这里插入图片描述

使用 $i, j$ 来索引通道， $\alpha$ 是每个项目的系数：
在这里插入图片描述

在重新定义方程1中所描述的星操作后，可以将其展开为 $\frac{(d+2)(d+1)}{2}$ 个不同的项，如方程4所示。除了$ \alpha_{(d+1,∶)}x^{d+1}x $外，每个项都与$ x $存在非线性关联，表明它们是独立的、隐含的维度。因此，在一个$ d$维空间内使用计算效率高的星操作进行计算，但在一个 $\frac{(d+2)(d+1)}{2} ≈ (\frac{d}{\sqrt{2}})^2$ （考虑到 $d ≫ 2$ ）的隐含维度特征空间中获得表示，显著增加了特征维度，而在单个层内不会产生额外的计算开销。

3、Generalized to multiple layers

堆叠多层，以递归方式指数增加隐含维度，接近无限。

考虑一个初始网络层的宽度为 $d$ ，应用一个星操作得到表达式 $\sum^{d+1}_{i=1} \sum^{d+1}_{j=1} w^{i}_{1}w^{j}_{2}x^{i}x^{j}$ ，如公式3所述。这导致在一个隐含特征空间中的表示为 $R(\frac{d}{\sqrt{2}})^{2^{1}}$ 。设 $O_{l}$ 表示第 $l$ 个星操作的输出，得到：

$O_{1} = \sum^{d+1}_{i=1} \sum^{d+1}_{j=1} w^{i}_{(1,1)}w^{j}_{(1,2)}x^{i}x^{j} \in R(\frac{d}{\sqrt{2}})^{2^{1}}, \ (6)$
$O_{2} = W^{T}_{2,1} O_{1} * W^{T}_{2,2} O_{1} \in R(\frac{d}{\sqrt{2}})^{2^{2}} ,\ (7)$
$O_{3} = W^{T}_{3,1} O_{2} * W^{T}_{3,2} O_{2} \in R(\frac{d}{\sqrt{2}})^{2^{3}} ,\ (8)$
$\ (9)$
$O_{l} = W^{T}_{l,1} O_{l-1} * W^{T}_{l,2} O_{1-1} \in R(\frac{d}{\sqrt{2}})^{2^{l}}. \ (10)$

通过 $l$ 层，可以隐式地获得一个属于 $R(\frac{d}{\sqrt{2}})^{2^{l}}$ 的特征空间。例如，给定一个宽度为128的10层各向同性网络，通过星操作获得的隐式特征维数大约为901024，可以合理地近似为无限维度。因此，通过堆叠多个层，即使只是几层，星操作可以以指数方式显著放大隐式维度。

4、Special Cases

情况I:W1和/或W2的非线性特性。

情况II:WT1 X∗ X。当移除转换W2时，隐式维度数量从大约 $\frac{d^{2}}{2}$ 减少到 $2 d$ 。

情况III:X∗ X。在这种情况下，星操作将特征从特征空间 ${x^{1},x^{2},⋯,x^{d}} \in R^{d}$ 转换为由 ${x^{1}x^{1},x^{2}x^{2},⋯,x^{d}x^{d}} \in R^{d}$ 表征的新空间。

星操作及其特殊情况通常（尽管不一定）与空间交互集成。通常通过池化或卷积实现，如VAN（Guo等，2023年）中所示。许多这些方法强调扩展感受野的好处，但往往忽视隐式高维空间所带来的优势。其次，将这些特殊情况结合起来是可行的，如Conv2Former （Hou等，2022年）展示的，它融合了情况I和情况II的特点，以及GENet-θ− （Hu，2018年）中展示的，它融合了情况I和情况III的元素。最后，尽管情况II和情况III可能不会显著增加单个层中的隐式维度，但线性层的使用（主要用于通道通信）和跳跃连接可以在多个层中累积实现高隐式维度。

5、Empirical Study

Empirical superiority of star operation

如图1 所示，作者构建了一个各向同性网络，称为DemoNet，用于进行演示。DemoNet 设计简单明了，包括一个通过卷积层将输入分辨率降低16 倍的层，然后是一系列用于特征提取的同质演示块（参见图1，左侧）。在每个演示块中，我们应用星操作或求和操作来融合来自两个不同分支的特征。通过改变网络的宽度和深度，探索了每种操作的独特属性。DemoNet 的实现细节在附录的算法1 中提供。
在这里插入图片描述

在这里插入图片描述

从表2 和表3 中，可以看到星操作在网络深度和宽度不同的情况下始终优于求和操作。这一现象验证了星操作的有效性和优越性。此外，观察到随着网络宽度的增加，星操作带来的性能增益逐渐减少。然而，在深度变化的情况下没有观察到类似的现象。这种行为上的差异暗示了两个关键见解：1）如表2 所示，星操作带来的性能增益逐渐减少并非模型尺寸增大的结果；2）基于此，这意味着星操作本质上扩展了网络的维度，从而减少了扩展网络带来的增量收益。
在这里插入图片描述

Decision Boundary comparison

通过视觉分析和辨别星号和求和操作之间的差异。为此，在玩具2D月球数据集[43] 上可视化这两种操作的决策边界，该数据集包含两组月球形状的2D点。在模型配置方面，从演示块中消除了归一化和卷积层。鉴于这个数据集相对简单的特性，将模型配置为宽度为100，深度为4。

图2（顶行）展示了由求和和星号操作勾勒出的决策边界。与求和操作相比，星号操作勾勒出了一个更加精确和有效的决策边界。决策边界的差异并非源自非线性，因为这两种操作都在各自的构建模块中包含激活函数。主要区别在于星号操作能够达到极高的维度。图2（底行）中展示了带有高斯核和多项式核的SVM的决策边界（使用scikit-learn 软件包实现[43]）。符合预期，星号操作产生的决策边界与多项式核的非常相似，而与高斯核明显不同。
在这里插入图片描述

通过从DemoNet中移除所有激活函数进行实验，从而创建一个无激活函数的网络。表4中的结果表明，当移除所有激活函数时，求和操作的性能显著下降，从66.2%降至32.4%。相比之下，星操作仅在准确率下降了仅1.2%，表明消除激活函数对星操作影响很小。

6、Open Discussions & Broader Impacts

I. 激活函数是否真的不可或缺？

星操作还包含非线性，这是区分核函数与其他线性机器学习方法的特征。研究中的初步实验展示了在神经网络中消除激活层的潜在可行性。

II. 星操作如何与自注意力和矩阵乘法相关？

自注意力利用矩阵乘法生成 $R^{n \times n}$ 中的矩阵。可以证明自注意力中的矩阵乘法与逐元素乘法具有相似的属性（非线性和高维度）。矩阵乘法促进了全局交互，与逐元素乘法形成对比。然而，矩阵乘法改变了输入形状，需要额外的操作（例如池化，另一轮矩阵乘法等）来调整张量形状，这是逐元素乘法所避免的复杂性。PolyNL [2]在这方面提供了初步努力。作者分析可能为自注意力的有效性提供新的见解，并有助于重新审视神经网络中的“动态”特征[7, 8, 12]。

III. 如何优化隐式高维空间中的系数分布？

传统神经网络可以为每个通道学习一组不同的权重系数，但星操作中每个隐式维度的系数，类似于核函数，是固定的。例如，在多项式核函数 $k(x_{1},x_{2}) =(\gamma x_{1} \cdot x_{2} + c)^{d}$ 中，系数分布可以通过超参数进行调整。在星操作中，虽然权重 $W_{1}$ 和 $W_{2}$ 是可学习的，但它们仅提供有限的范围来微调分布，与传统神经网络中为每个通道定制系数的做法相反。这种约束可能解释了为什么极高维度只会带来适度的性能改进。值得注意的是，跳跃连接似乎有助于平滑系数分布 [57]，而密集连接（如DenseNet [32]）可能提供额外的好处。此外，使用指数函数可以提供到隐式无限维度的直接映射，类似于高斯核函数。

四、实验Proof-of-Concept: StarNet

引入StarNet作为一个概念验证模型。StarNet的特点是极其简约的设计和人为干预的显著减少。尽管简单，StarNet展示了出色的性能，突显了星操作的有效性。

StarNet Architecture

StarNet由一个4阶层次结构构建而成，利用卷积层进行下采样和修改后的demo块进行特征提取。为了满足效率要求，用Batch Normalization替换Layer Normalization，并将其放置在深度卷积之后（在推断期间可以融合）。受MobileNeXt[66]的启发，在每个块的末尾加入了深度卷积DW Conv。通道扩展因子始终设置为4，在每个阶段网络宽度翻倍。在demo块中，GELU激活被替换为ReLU6，遵循MobileNetv2 [46]的设计。StarNet框架如图3所示。仅变化块数和输入嵌入通道数以构建
不同大小的StarNet，详见表5。
在这里插入图片描述

Experimental Results

遵循DeiT的标准训练配方 [53]，以确保在训练StarNet模型时进行公平比较。所有模型均从头开始训练300个epochs，使用AdamW优化器 [39]，初始学习率为3e-3，批量大小为2048。详细的训练细节请参见补充材料。为了进行基准测试，将PyTorch模型转换为ONNX格式 [13]，以便在CPU（Intel Xeon CPU E5-2680 v4 @ 2.40GHz）和GPU
（P100）上进行延迟评估。此外，使用CoreML-Tools [1]在iPhone13上部署模型，以评估移动设备上的延迟。这些基准测试的详细设置也可在补充材料中找到。
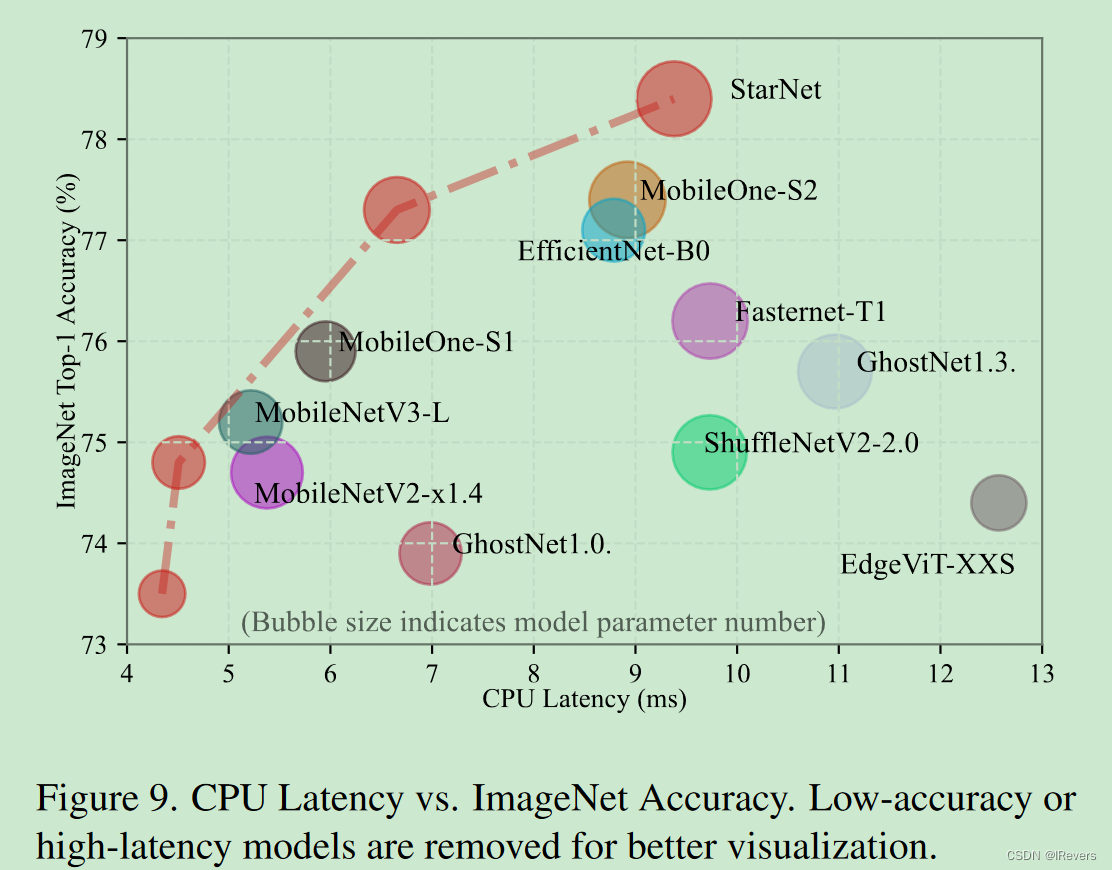
在这里插入图片描述

在这里插入图片描述

StarNet在iPhone 13设备上仅用0.7秒就实现了73.5%的top-1准确率，在相同的延迟下超过MobileOne-S0 2.1%（73.5% vs. 71.4%）。当将模型扩展到1G FLOPs预算时，StarNet继续展现出卓越的性能，超过MobileOne-S2 1.0%，并超过EdgeViT-XS0.9%，同时速度快三倍（1.0毫秒 vs. 3.5毫秒）。

在这里插入图片描述

图4 进一步说明了各种模型之间的延迟-准确性权衡。如果能进一步提升StarNet的性能？相信通过仔细的超参数优化，利用表1中的见解，并应用更多的epochs或蒸馏等训练增强措施，可以大幅提升StarNet的性能。

More Ablation studies

替换星操作
在这里插入图片描述

移除所有星操作导致显著的性能下降，观察到3.1%的准确率下降。星操作对性能的影响在模型的第一和第二阶段中似乎很小。这一观察是合乎逻辑的。由于ReLU6激活具有非常窄的宽度，一些特征会变为零。在星操作的背景下，这导致其隐式高维空间中的许多维度也变为零，从而限制了其全部潜力。然而，在最后两个阶段（更多通道）中，其贡献变得更加显著，分别导致1.6%和1.6%的改进。表7中的最后三行也验证了该结论。
在这里插入图片描述

在这里插入图片描述

星操作的延迟影响
在这里插入图片描述

进行了基准测试，比较了用求和替换所有星操作的延迟，结果详见表8。从观察到延迟影响取决于硬件。在实践中，星操作相对于求和操作在GPU和iPhone设备上并未导致额外的延迟。然而，在CPU上，求和操作比星操作稍微更有效率（例如，对于StarNet-S4，8.4ms vs.9.4ms）。鉴于显著的性能差距，CPU上的这种轻微延迟开销可以被视为可以忽略的。

激活位置的研究
在这里插入图片描述

$x_{1}$ 和 $x_{2}$ 被用来表示两个分支的输出，其中StarNet-S4 作为实验模型。研究了四种在StarNet中实现激活函数的方法：1）不使用激活，2）激活两个分支，3）在星操作后激活，4）激活单个分支(默认做法)。如表9所示的结果表明，仅激活一个分支可以获得最高准确率，达到了78.4%。从StarNet 中完全移除激活（除了干细胞层中的一个）仅导致准确率下降了2.8%，降至75.6%，这一性能仍然与表6中一些强基线相竞争。这些发现与表4一致，强调了无激活网络的潜力。

关于星操作块设计的研究
在StarNet中，星操作通常被实现为 $act(W^{T}_{1} X) ∗ (W^{T}_{2} X)$ 。这种标准方法使得StarNet-S4的准确率达到了84.4%。然而，也存在替代实现方式。作者尝试了一种变体： $(W^{T}_{2} act(W^{T}_{1} X)) ∗ X$ ，其中 $W_{1} \in R^{d \times d′}$ 被设计用于扩展宽度，而 $W_{2} \in R^{d′ \times d}$ 将其恢复回 $d$ 。这种调整导致了仅一个分支的转换，而另一个保持不变。变化 $d'$ 以确保与StarNet-S4相同的计算复杂度。通过这样做，性能从78.4%下降到了74.4%。虽然更好和谨慎的设计可能会缓解这种性能差距（见附录），但准确率上的显著差异强调了最初实现中利用星操作能力的有效性，并强调了在星操作中转换两个分支的关键重要性。

五、总结

作者重新定义了星操作，揭示出它们强大的表征能力源自隐含的高维空间。在许多方面，星操作反映了多项式核函数的行为。通过经验、理论和可视化方法得到了严格验证，结果在数学和理论上是一致的。并引入了一个简单的原型网络StarNet。StarNet的出色性能，不依赖于复杂的设计或精心选择的超参数，为对星操作的探索开辟了许多潜在的研究方向。