北航第四次数据结构与程序设计编程题复习

到期末了，所以再来复习一下以前的作业。

北航第四次数据结构与程序设计编程题

一、栈操作（栈-基本题）
二、C程序括号匹配检查
三、计算器（表达式计算-后缀表达式实现，结果为浮点）
四、文本编辑操作模拟（简）a
五、银行排队模拟（生产者-消费者模拟） - 分类别

一、栈操作（栈-基本题）

【问题描述】

假设给定的整数栈初始状态为空，栈的最大容量为100。从标准输入中输入一组栈操作，按操作顺序输出出栈元素序列。栈操作：1表示入栈操作，后跟一个整数（不为1、0和-1）为入栈元素；0表示出栈操作；-1表示操作结束。

【输入形式】

从标准输入读取一组栈操作，入栈的整数和表示栈操作的整数之间都以一个空格分隔。

【输出形式】

在一行上按照操作的顺序输出出栈元素序列，以一个空格分隔各元素，最后一个元素后也要有一个空格。如果栈状态为空时进行出栈操作，或栈满时进行入栈操作，则输出字符串“error”，并且字符串后也要有一空格。所有操作都执行完后，栈也有可能不为空。

【样例输入】

1 3 1 5 1 7 0 0 1 8 0 1 12 1 13 0 0 0 0 1 90 1 89 0 -1

【样例输出】

7 5 8 13 12 3 error 89

【样例说明】

入栈元素依次为3、5、7，然后有两次出栈动作，所以先输出7和5，这时栈中只有元素3；之后元素8入栈，又出栈，输出8；随后元素12和13入栈，再进行4次出栈操作，输出13、12和3，这时栈为空，再进行出栈操作会输出error；最后90和89入栈，进行一次出栈操作，输出89，栈中剩余1个元素。

【评分标准】

该题要求按照操作的顺序输出出栈元素序列，提交程序名为stack.c。

本题的思路就是：输入1，后面接一个入栈元素；输入0，则进行弹栈操作；栈满输入和栈空弹栈，都输出error。
因此可以用一个flag变量来记录第一个输入的数字，以此判断入栈还是弹栈，然后再判断接下来要不要继续输入元素。
如果flag显示为结束标志符即-1，则结束输入。

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define MAX 100
int arr[100],Top=-1;
enum ope {PUSH=1,POP=0,END=-1};
int isFull()
{
    return Top==MAX;
}
int isEmpty()
{
    return Top==-1;
}
void Push(int x)
{
    if(isFull())
    {
        printf("error ");  
        return;
    }
    arr[++Top]=x;
}
int Pop()
{
    if(isEmpty())
    {
        printf("error ");
        return 0;
    }
    return arr[Top--];
}
int main()
{
    enum ope flag;
    scanf("%d",&flag);
    int item;
    while(flag!=END)
    {
        if(flag==PUSH)
        {
            scanf("%d",&item);
            Push(item);
        }
        else if(flag==POP)
        {
            int pop=Pop();
            if(pop!=0)
                printf("%d ",pop);
        }
        scanf("%d",&flag);
    }
}

这里有两个小tip：

enum ope {PUSH=1,POP=0,END=-1};建议大家多用枚举类型，这道题里面因为只有1,0，-1三个标志符，而且代码量不大，所以你觉得没什么问题，那万一有10个20个标志符呢？单纯的1,2,3,4…会让代码的可读性大大下降，用这种方式，在调试的时候会非常容易知道操作类型。
scanf("%d",&flag);代码循环里的这一个也需要注意一下，不要在%d后面加一个空格，因为读到最后一个数，也就是-1的时候，-1的后面不一定有空格，那么我们的程序在读到-1的时候，如果读不到后面的空格，程序就进行不完，因此不需要在scanf里带空格。因为我们现在读的是整型，scanf识别的空格会自动跳过的。

二、C程序括号匹配检查

【问题描述】

编写一程序检查C源程序文件中{}、()等括号是否匹配,并输出第一个检测到的不匹配的括号及所对应括号所在的行号（程序中同一类括号只有一个不匹配）。

注意：

1.除了括号可能不匹配外，输入的C源程序无其它语法错误。

2.字符常量、字符串常量及注释中括号不应被处理，注释包括单行注释//和多行/* */注释

3.字符常量和字符串常量中不包含转义字符’和"；

4.程序中出现有意义括号的个数不超过200个；

不匹配判断规则：

1.当检测的程序括号为’{‘时，若其前序尚未匹配的括号为’(‘时，输出该’('左括号及所在行号；

2.当遇到一个不匹配的右括号’)‘或’}'时，输出该右括号及所在行号；

3.当程序处理完毕时，还存在不匹配的左括号时，输出该左括号及所在行号。

【输入形式】

打开当前目录下文件example.c，查询其括号是否匹配。该文件中每行字符数不超过200。

【输出形式】

若存在括号不匹配时，应输出首先能判断出现不匹配的括号及其所在的行号。当出现括号不匹配时，按下面要求输出相关信息：

without maching < x > at line < n >

其中< x >为‘{’, ‘}’， ‘(’, ‘)’等符号，< n >为该符号所在的行号。

若整个程序括号匹配，则按下面所示顺序输出括号匹配情况，中间没有空格。

(){(()){}}

【样例输入1】

若当前目录下输入文件example.c中内容如下：

#include<stdio.h>

int main(){

printf(“{ hello world }\n”); // }

)

【样例输出1】

without maching ‘)’ at line 4

【样例输入2】

若当前目录下输入文件example.c中内容如下：

#include<stdio.h>

int main(){

printf(“{ hello world }d\n”); /* }*/

【样例输出2】

without maching ‘{’ at line 2

【样例输入3】

若当前目录下输入文件example.c中内容如下：

#include<stdio.h>

int main(){

printf(“{ hello world }d\n”); /* }*/

}

【样例输出3】

(){()}

【样例说明】

样例1：在注释部分和字符串中的括号不考虑，在将程序处理之后得到的括号序列是（）{（）），遇到右括号时与最近的左括号匹配，发现最后一个小括号和大括号不匹配。

样例2：处理之后的括号序列是（）{（），在最后缺少了右大括号，那么应该输出与之相对应的左括号不匹配。

【评分标准】

通过所有测试点得满分。
做这个题之前可以看看link我的这篇问斩里的一个题：括号匹配问题，是这个问题的简化版，因为输出的字符串只包含（）{ } [ ]，但这道题就相对比较复杂了。

先来说几个注意点：

如果括号简化一后为 { ），那其实这两个括号都不匹配，但是，输出还得是），因为遍历到 { 的时候，我们并不知道程序后面还有没有跟他匹配的 } ,但是一个右括号，前面没有一个匹配左括号，那显然直接就可以判断不匹配。不匹配规则2说的意思也是这个。
多行注释需要注意：
/* ……
* ……
* ……
* /
*的前后都不一定是/。
四种情况下，不需要让括号入栈：
单行注释//
多行注释/**/
单引号
双引号，如果碰到了这些情况，则直接让循环一直++到注释或引号结束。
遇到 { ，如果栈空直接入栈，否则判断栈顶是否是（，是的话，输出（还有他的行数，不是的话，{ 入栈。

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
typedef struct 
{
    char item;
    int line;
}bracket;

char all_brackets[100];
bracket judge_match[100];
int Top=-1;
int Topall=-1;
int main()
{
    FILE* fp=fopen("example.c","r");
    int ch;
    int line=1;
    while((ch=fgetc(fp))!=EOF)
    {
        //{
        if(ch=='{')
        {
            if(Top>-1&&judge_match[Top].item=='(')
            {
                printf("without matching '(' at line %d",judge_match[Top].line);
                return 0;
            }
            else
            {
                Top++;
                judge_match[Top].item='{';
                judge_match[Top].line=line;
                all_brackets[++Topall]='{';
            }
        }
        //}
        else if(ch=='}')
        {
            if(Top==-1)//空栈
            {
                printf("without matching '}' at line %d",line);
                return 0;
            }
            else if(judge_match[Top].item!='{')
            {
                printf("without matching '}' at line %d",line);
                return 0;
            }
            else
            {
                all_brackets[++Topall]='}';
                Top--;
            }
        }
        //(
        else if(ch=='(')
        {           
            Top++;
            judge_match[Top].item='(';
            judge_match[Top].line=line;
            all_brackets[++Topall]='(';
        }
        //)
        else if(ch==')')
        {
            if(Top==-1)//空栈
            {
                printf("without matching ')' at line %d",line);
                return 0;
            }
            else if(judge_match[Top].item!='(')
            {
                printf("without matching ')' at line %d",line);
                return 0;
            }
            else
            {
                all_brackets[++Topall]=')';
                Top--;
            }
        }
        //\n
        else if(ch=='\n')
        {
            line++;
        }
        //单引号情况
        else if(ch=='\'')
        {
            while((ch=fgetc(fp))!='\'')
                continue;
            fseek(fp,-1,SEEK_CUR);
        }
        //双引号
        else if(ch=='\"')
        {
            while((ch=fgetc(fp))!='\"')
                continue;
        }
        //单行注释与多行注释
        else if (ch=='/')
        {
            int back=fgetc(fp);
            if(back=='/')//单行注释
            {
                back=fgetc(fp);
                while(!(back=='\n'||back==EOF))
                {
                    back=fgetc(fp);
                }
                line++;
            }
            else if(back=='*')//多行注释，内部如果检测到\n需要对行数加一
            {              
                back=fgetc(fp);
                int back1=fgetc(fp);
                while(1)
                {
                    if(back=='\n')
                    {
                        line++;
                        back=back1;
                        back1=fgetc(fp);
                    }
                        
                    else
                    {
                        if(back=='*'&&back1=='/')
                            break;
                        else
                        {
                            back=back1;
                            back1=fgetc(fp);
                        }
                    }
                }
            }
        }
        //字符或数字不用考虑，直接进行下一次循环
    }
    if(Top!=-1)
    {
        printf("without matching '%c' at line %d",judge_match[0].item,judge_match[0].line);
        return 0;
    }
    for(int i=0;i<Topall+1;i++)
    {
        printf("%c",all_brackets[i]);
    }
    return 0;
}

ch是我们访问到的字符，把遇到每一种字符需要进行的操作都标注起来了，在每一个if语句的上面注释。每一种都略有不同，但都必须依据题目给的三条判断规则来。
另外，对于注释和引号的判断可能略有难度，大家画图理解指针的变换会更好一点，理解清楚为什么我在有些地方加了fseek（fp，-1，SEEK_CUR），而有些地方没加，你就懂得差不多了。

三、计算器（表达式计算-后缀表达式实现，结果为浮点）

【问题描述】

从标准输入中读入一个算术运算表达式，如：24 / ( 1 + 5/3 + 36 / 6 / 2 - 2) * ( 12 / 2 / 2 )= ，计算表达式结果，并输出。

要求：

1、表达式运算符只有+、-、*、/，表达式末尾的=字符表示表达式输入结束，表达式中可能会出现空格；
2、表达式中会出现圆括号，括号可能嵌套，不会出现错误的表达式；

3、表达式中出现的操作数都是十进制整数常量；但要求运算结果为浮点型，例如：5/2结果应为2.5。

4、要求采用逆波兰表达式来实现表达式计算。

【输入形式】

从键盘输入一个以=结尾的算术运算表达式。操作符和操作数之间可以有空格分隔。

【输出形式】

在屏幕上输出计算结果，小数点后保留两位有效数字。

【样例输入】

24 / ( 1 + 5/3 + 36 / 6 / 2 - 2) * ( 12 / 2 / 2 ) =

【样例输出】

19.64
【样例说明】

按照运算符及括号优先级依次计算表达式的值。

【评分标准】

该题要求采用逆波兰表达式实现表达式运算，提交程序名为cal.c。

这道题有两个大的步骤，一个是中缀表达式转为后缀表达式，即逆波兰表达式。第二步就是计算逆波兰表达式的值。

先来回顾一下中缀表达式转后缀表达式的步骤：
1.遇到计算数，直接输入后缀表达式
2.遇到计算符，以下情况直接入运算符栈：a.运算符栈为空 b.运算符栈不为空，且栈顶元素为（或栈顶元素优先级小于该计算符。以下情况不可直接入栈：栈顶元素优先级大于等于该运算符时，栈顶运算符出栈，输入到后缀表达式中（注意不要和直接计算中缀表达式搞混），然后再判断该计算符和当前栈顶元素优先级，重复以上操作直到遇见（或者优先级小于它的运算符。
3.遇到左括号直接入栈。
4.遇到右括号，则从栈顶开始依次将运算符输入到后缀表达式中，直到遇到左括号，左括号出栈但不输入到后缀表达式中。
注意：不要和直接计算中缀表达式搞混。

接下来是计算后缀表达式：
1.遇到运算数，放入运算数栈中。
2.遇到运算符，弹出栈顶两个元素进行运算。
3.后缀表达式无括号

那么我们怎样才能把浮点类型的运算数和字符类型的运算符放到同一个数组中呢？
这就要用到我们的联合了。
我们定义一个结构体，然后再创立一个这个结构体类型的数组，用于存放后缀表达式。

enum set {OP,NUM};
typedef struct item
{
    enum set type;
    union
    {
        char ope;
        float num;
    }uni;
}ITEM;

结构体成员type用于区分运算数和运算符，uni用于记录运算符和运算数的具体值。

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
enum set {OP,NUM};
typedef struct item
{
    enum set type;
    union
    {
        char ope;
        float num;
    }uni;
}ITEM;
void remove_zero(char*);去掉原始表达式中出现的空格
void toReversePoland(char*);这个函数用于把中缀表达式转换成后缀
void CalExpess(ITEM*,int);这个用于计算后缀表达式的值
int Priority(char);判断优先级
int main()
{
    char ch='a';
    char arr[100];
    gets(arr);
    
    remove_zero(arr);
    toReversePoland(arr);
    return 0;
}
void remove_zero(char* a)
{
    int i=0,j=0;
    while(a[j]!='\0')
    {
        if(a[j]!=' ')
        {
            a[i]=a[j];
            j++;
            i++;
        }
        else
            j++;
    }
    a[i]='\0';
}
void toReversePoland(char* a)
{
    ITEM arr[100];
    int index=0;
    char operation[100];
    int Top=-1;

    for(int i=0;i<strlen(a);i++)
    {
        if(a[i]>='0'&&a[i]<='9')
        {
            float num=a[i]-'0';
            for(int j=i+1;j<strlen(a);j++)
            {
                if(a[j]>='0'&&a[j]<='9')
                {
                    num=num*10+(a[j]-'0');
                }
                else
                {
                    arr[index].type=NUM;
                    arr[index].uni.num=num;
                    i=j-1;
                    index++;
                    break;
                }
            }
        }
        else if(a[i]=='=')
            break;
        else if(a[i]=='+'||a[i]=='-'||a[i]=='*'||a[i]=='/')
        {
            if(Top==-1)
                operation[++Top]=a[i];
            else
            {
                while(Top>-1&&operation[Top]!='('&&(Priority(operation[Top])>=Priority(a[i])))
                {
                    arr[index].type=OP;
                    arr[index].uni.ope=operation[Top];
                    index++;
                    Top--;
                }
                operation[++Top]=a[i];
            }
        }
        else if(a[i]=='(')
        {
            operation[++Top]='(';
        }
        else if(a[i]==')')
        {
            char top=operation[Top];
            while(top!='(')
            {
                arr[index].type=OP;
                arr[index].uni.ope=top;
                index++;
                Top--;
                top=operation[Top];
            }
            Top--;
        }
    }
    while(Top!=-1)
    {
        arr[index].type=OP;
        arr[index].uni.ope=operation[Top];
        index++;
        Top--;
    }
    // for(int i=0;i<index;i++)
    // {
    //     if(arr[i].type==OP)
    //         printf("%c ",arr[i].uni.ope);
    //     else
    //         printf("%.2f ",arr[i].uni.num);
    // }
    CalExpess(arr,index);
}
int Priority(char a)
{
    if(a=='+'||a=='-')
        return 1;
    if(a=='*'||a=='/')
        return 2;
}
void CalExpess(ITEM* a,int n)
{
    float num[100];
    int Top=-1;
    for(int i=0;i<n;i++)
    {
        if(a[i].type==NUM)
        {
            num[++Top]=a[i].uni.num;
        }
        else
        {
            if(a[i].uni.ope=='+')
            {
                float x=num[Top];
                Top--;
                float y=num[Top];
                num[Top]=x+y;
            }
            else if(a[i].uni.ope=='-')
            {
                float x=num[Top];
                Top--;
                float y=num[Top];
                num[Top]=y-x;
            }
            else if(a[i].uni.ope=='*')
            {
                float x=num[Top];
                Top--;
                float y=num[Top];
                num[Top]=x*y;
            }
            else if(a[i].uni.ope=='/')
            {
                float x=num[Top];
                Top--;
                float y=num[Top];
                num[Top]=y/x;
            }
        }
    }
    printf("%.2f",num[0]);
}

我在toReversePoland函数里插入了这样一段代码：

 // for(int i=0;i<index;i++)
    // {
    //     if(arr[i].type==OP)
    //         printf("%c ",arr[i].uni.ope);
    //     else
    //         printf("%.2f ",arr[i].uni.num);
    // }

这个用于打印出转换后的逆波兰表达式，便于查找我们的问题所在。

同样，在第一次做这个作业的时候我把栈的整个数据结构都敲进去了，但是这一次做我没有明确的规定栈，只建立一个数组，用到先进先出的思想就ok。但作为初学者的话，每次都敲一遍有助理解。

四、文本编辑操作模拟（简）a

【问题描述】

编写一程序模拟文本编辑操作。首先从标准输入读取一行字符串（字符个数不超过512），该行字符串是已经过n（大于0，小于等于10）步编辑操作后的结果。然后从下一行读取n，以及已发生过的n步编辑操作，编辑操作分行输入，输入格式为：

op pos str

其中op为编辑操作命令编码（在此只有插入和删除操作，1表示插入或2表示删除操作）；pos表示插入或删除的位置；str表示已经插入或删除的字符串（中间没有空格）。各数据间以一个空格分隔。

然后在空一行后，再分行输入当前将要进行的编辑操作，包括如下四种操作（操作编码分别为：1表示插入，2表示删除操作，3表示撤销（即undo操作），-1表示结束）：

1 pos str

表示将在pos位置插入字符串str（中间没有空格），各数据间以一个空格分隔；

2 pos n

表示将从pos位置开始删除n个字符（各数据间以一个空格分隔），若要删除的字符个数多于已有字符个数（即在文本中从pos开始的字符个数小于n），则按实际字符数删除即可。（提示：为了能够撤销删除操作，应按“2 pos str”形式保存命令。）

表示撤销最近执行的插入或删除操作，可以进行多次撤销操作，注意：也可以撤销之前已经发生过的n步编辑操作中的操作。

-1

表示退出编辑操作，在屏幕上输出最终编辑后的文本。

要求：

1、上述所有输入的编辑操作中的字符串str都不包含空白字符（空格符、制表符或换行符）；

2、插入操作中的位置pos大于等于0，并且小于等于当前文本的字符个数；0位置表示文本第一个字符的位置；若pos为当前文本的字符个数，则表示在文本最后插入字符串；

3、删除操作中的位置pos大于等于0，并且小于当前文字的字符个数；

4、若已无操作可撤销，则再进行撤销操作无效；

5、文本在编辑过程中，总字符个数不会超过512。

【输入形式】

先从键盘输入一行字符串，表示已经经过n步编辑操作后的文本串，然后在下一行输入一个正整数n，并分行输入n步插入或删除操作（表示按时间先后顺序已进行的操作），格式如上所述。随后空一行，再分行输入将要进行的编辑操作，格式如上所述。直到输入-1操作为止。

【输出形式】

在屏幕上输出最终编辑后的文本内容。

【样例输入】

A Stack is a container of objects that are inserted and removed according to the last-in first-out (LIFO) principle.???

1 20 ainer

2 0 ???

1 85 -

1 99 (LIFO)

2 110 10

1 110 Objects

2 98 1

2 0 1

2 108 10

-1

【样例输出】

A Stack is a container of objects that are inserted and removed according to the last-in first-out principle.Objects

【样例说明】

第一行输入的文本串是先后经过下面4次编辑操作后得到的：先在20位置插入了字符串ainer，然后删除了开始位置的字符串???，随后在85位置插入了一个字符-，最后在99位置插入了字符串(LIFO)。

随后输入了撤销操作，即撤销先前最后进行的“1 99 (LIFO)”操作，也就是将99位置的6个字符删除；

2 110 10：将文本串最后的字符串???删除；

1 110 Objects：在文本串末尾插入字符串Objects；

随后执行了三次删除操作，又执行了三次撤销操作，最后输入的-1表示编辑操作结束，在屏幕上输出最终编辑后的文本串。

【评分标准】

该程序要求编程模拟编辑操作，提交程序文件名为edit.c。

这个题是一个经典的要用到栈的题，其中操作1、2代表入栈，3代表出栈。栈内元素类型我们依然用一个结构体来表示：

typedef struct item
{
    int type;
    int pos;
    char arr[100];
}OPE;

这个题需要绕一下的地方在于，入栈的时候，操作字符串是顺着来，比如你写了一个函数insert用于对字符串进行插入操作，那么输入3进行撤回的时候，就要调用delete函数了。

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
typedef struct item
{
    int type;
    int pos;
    char arr[100];
}OPE;
OPE stack[100]; 
char arr[600];
int top=0;
int flag=0;
void Insert(int,char*);
void Delete(int,int);
void Undo();
int main()
{
    gets(arr);

    int prev;
    scanf("%d",&prev);
    
    for(;top<prev;top++)
    {
        scanf("%d %d %s",&stack[top].type,&stack[top].pos,stack[top].arr);
    }

    int type;
    int pos;
    char inarr[100];
    int delnum;
    scanf("%d",&type);
    while(type!=-1)
    {
        if(type==1)
        {
            scanf("%d %s",&pos,inarr);
            Insert(pos,inarr);
        }
        else if(type==2)
        {
            scanf("%d %d",&pos,&delnum);
            Delete(pos,delnum);
        }
        else if(type==3)
        {
            flag=1;
            Undo();
            top--;
            flag=0;
        }
        scanf("%d",&type);
    }
    printf(arr);
}
void Insert(int pos,char* str)
{   
    if(flag==0)
    {
        stack[top].type=1;
        stack[top].pos=pos;
        strcpy(stack[top].arr,str);
        top++;
    }
    int len_all=strlen(arr);
    memmove(arr+pos+strlen(str),arr+pos,len_all-pos+1);
    strncpy(arr+pos,str,strlen(str));
}
void Delete(int pos,int delnum)
{
    if(flag==0)
    {
        int len_longest=strlen(arr)-pos;
        if(delnum>len_longest)
        delnum=len_longest;

        char delarr[100];
        strncpy(delarr,arr+pos,delnum);
        delarr[delnum]='\0';

        stack[top].type=2;
        stack[top].pos=pos;
        strcpy(stack[top].arr,delarr);
        top++;
    }
    memmove(arr+pos,arr+pos+delnum,strlen(arr)+1-pos-delnum);
}
void Undo()
{
    if(top==0)
        return;
    if(stack[top-1].type==1)
    {
        int delnum=strlen(stack[top-1].arr);
        Delete(stack[top-1].pos,delnum);
    }
    else
    {
        Insert(stack[top-1].pos,stack[top-1].arr);
    }
}

五、银行排队模拟（生产者-消费者模拟） - 分类别

【问题描述】

一个系统模仿另一个系统行为的技术称为模拟，如飞行模拟器。模拟可以用来进行方案论证、人员培训和改进服务。计算机技术常用于模拟系统中。

生产者-消费者（Server-Custom）是常见的应用模式，见于银行、食堂、打印机、医院、超市等提供服务和使用服务的应用中。这类应用的主要问题是消费者如果等待（排队）时间过长，会引发用户抱怨，影响服务质量；如果提供服务者（服务窗口）过多，将提高运管商成本。（经济学中排队论）

假设某银行网点有五个服务窗口，分别为三个对私、一个对公和一个外币窗口。银行服务的原则是先来先服务。通常对私业务人很多，其它窗口人则较少，可临时改为对私服务。假设当对私窗口等待服务的客户（按实际服务窗口）平均排队人数超过（大于或等于）7人时，等待客户将可能有抱怨，影响服务质量，此时银行可临时将其它窗口中一个或两个改为对私服务，当平均排队客户少于7人时，将立即恢复原有业务。设计一个程序用来模拟银行服务。

说明：

增加服务窗口将会增加成本或影响其它业务，因此，以成本增加或影响最小为原则来增加服务窗口，即如果增加一个窗口就能使得按窗口平均等待服务人数小于7人，则只增加一个窗口。一旦按窗口平均等待服务人数小于7人，就减少一个所增加的窗口。
为了简化问题，假设新到客户是在每个服务周期开始时到达。
根据客户业务服务时间将客户分为3类：1（简单业务）、2（普通业务）、3（复杂业务），分别对应花费1-3个时间周期。
当等待服务人数发生变化时（新客户到达或有客户已接受服务），则及时计算按实际服务窗口平均等待服务人数，并按相应策略调整服务窗口数（增加或减少额外的服务窗口，但对私窗口不能减少）。注意：**只在获取新客户（不管到达新客户数是否为0）时，才按策略调整服务窗口数。**进一步讲，增加服务窗口只在有客户到达的周期内进行（也就是说增加窗口是基于客户的感受，银行对增加窗口是不情愿的，因为要增加成本，一旦不再有新客户来，银行是不会再增加服务窗口的）；一旦有客户去接受服务（即等待客户减少），银行将根据策略及时减少服务窗口，因此，在每个周期内，有客户去接受服务后要马上判断是否减少服务窗口（因为能减少成本，银行是积极的）。

5.服务窗口的类别不固定，即：对私服务窗口也可根据需要转为对公或外币窗口。

本问题中假设对公和对外币服务窗口在改为对私服务时及服务期间没有相应因公或外币服务新客户到达（即正好空闲），同时要求以增加成本或影响最小为前提，来尽最大可能减少对私服务客户等待时间。

【输入形式】

首先输入一个整数表示时间周期数，然后下一行输入每个时间周期到达的客户人数；再依次分行输入每个时间周期到达的因私业务的客户类别。注：一个时间周期指的是银行处理一笔业务的平均处理时间，可以是一分钟、三分钟或其它。每行中的整数之间以一个空格分隔。

例如：

2 5 8 11 15 6

1 3

2 2 1 3 2

…

说明：共有6个时间周期，第1个周期来了2个客户（序号分别为1、2，业务分别为简单业务和复杂业务），第2个时钟周期来了5人（序号分别为3、4、5、6、7，业务分别为普通业务、普通业务、简单业务、复杂业务和普通业务），以此类推。

【输出形式】

每个客户等待服务的时间周期数。输出形式如下：

用户序号 : 等待周期数

说明：客户序号与等待周期数之间用英文冒号:分隔，冒号（:）两边各有一个空格，等待周期数后直接为回车。

【样例输入】

2 5 13 11

1 3

2 2 1 3 2

1 1 1 1 3 3 2 2 1 2 3 1 1

3 3 2 1 3 1 1 3 1 3 3

【样例输出】

1 : 0

2 : 0

3 : 0

4 : 0

5 : 2

6 : 2

7 : 2

8 : 1

9 : 2

10 : 3

11 : 3

12 : 4

13 : 4

14 : 4

15 : 6

16 : 7

17 : 7

18 : 8

19 : 8

20 : 9

21 : 8

22 : 9

23 : 10

24 : 11

25 : 12

26 : 12

27 : 12

28 : 13

29 : 13

30 : 14

31 : 15

【样例说明】

样例输入表明有四个时间周期，第一个周期来了2人（序号1-2）；第二个周期来了5人（序号3-7）；第三个周期来了13人（序号8-20）；第四个周期来了11人（序号21-31）。由于第一个时间周期内只来了2人，银行（有三个服务窗口）能及时提供服务，因此客户等待时间为0；第二个时间周期内来了5人，银行一个周期内一次只能服务3人，而且第一个周期内有一位办理复杂业务的客户，所以这时只有两个空闲窗口可以提供服务，前2人等待时间为0，另外3人需要等待；其它类推。

【评分标准】

通过所有测试点得满分。

我们先来解释下样例：
4（上面那一堆什么服务时间的解释都不要看，这个意思就是有客户来的周期。比如，可能要进行20次周期，所有的客户才能被服务完，那么有新顾客到的只有前4个周期，后面的20-4个周期只有排队中的客户，而没有新到银行的客户）

2 5 13 11（第一个周期来2个客户，第二个周期5个，第三个周期13个，第四个周期11个）

1 3（①号用户办理1号业务，②号客户办理3号业务）

2 2 1 3 2（③号办理2号业务，④号办理2号业务，⑤号办理1号业务，⑥号办理3号业务……）

1 1 1 1 3 3 2 2 1 2 3 1 1（以此类推）

3 3 2 1 3 1 1 3 1 3 3
再来画一个图来解释一下这道题，属实有点费脑子：
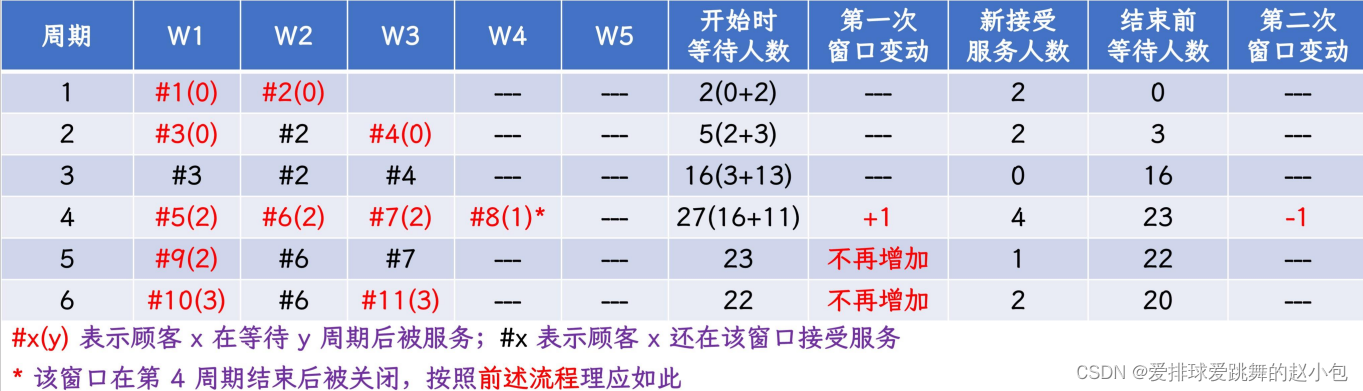在这里插入图片描述（此图为助教提供，非作者原创）
看第一行：开始时等待人数指的是第n周期开始的时候有几个人在排队，那么第一周期开始时又两人在排队，此时3个私人窗口均空闲，则直接办理业务，等待周期为0。那么这个周期里，新接受服务的人也是2。结束前等待人数指的是第一周期结束时，还在排队的人数，那么显然为0；

第二行：新来了5个人在排队，开始时等待人数为5，空闲窗口为两个，其中2号窗口还在为2号客户办理3号业务。那么客户3和客户4可以不用排队，直接到1号和3号窗口，即第二周期新接受服务人数为2，那么结束前等待人数就为3，分别是5、6、7号客户。

第三行：第三周期新来了13个人，开始时等待人数为3+13，因为第二周期结束的时候还有5、6、7三个客户在排队。此时，1号窗口在给3号客户办理2号业务，2号窗口在给2号客户办理3号业务，3号窗口在给4号客户办理2号业务，没有空闲窗口，且平均排队人数没有超过7。第三周期新接受服务人数为0，结束时排队人数为13+3=16。

第四行：第四周期新来了11个人，开始时等待人数为11+16=27个人。此时实际服务窗口为3个，则平均排队人数为：27/3=9>7，那么增开一个窗口时：27/4 < 7，所以开4个窗口就OK。这一周期，前面办理业务的都办完了，4个窗口都空闲，所以队伍中的5、6、7、8号客户办理业务。新接受服务人数为4，结束时等待人数为27-4=23。根据题目中的这一句话：**“一旦有客户去接受服务（即等待客户减少），银行将根据策略及时减少服务窗口，因此，在每个周期内，有客户去接受服务后要马上判断是否减少服务窗口。”**在这一周期结束的时候，我们就需要判断窗口是否要减少了。此时排队人数为23，窗口数为4,23/4 < 7，因此关闭一个窗口。

第五行：根据题目中的这一句话：增加服务窗口只在有客户到达的周期内进行。此时已经到了第五周期，而有新客户到来的周期是1-4，所以此时不需要再增加窗口。在接下来的周期中，只需要判断3个私人窗口是否空闲，然后客户补足位置即可。

每个客户有三个基本属性：排队号、等待时间、业务类型。其中，前两个放在客户结构体中，业务类型还要体现在窗口的剩余时间上。

#define MAXSIZE 100
#define THRESHOLD 7//窗口增加阈值
#define MAXSVR 5//最大服务窗口数
#define MINSVR 3//最小服务窗口数
typedef struct
{
    int id;//客户排队号
    int wtime;//客户等待周期数
    int contact;//业务类型
}CustType;
CustType Cqueue[100];//等待服务的客户队列，一个循环队列
int Winnum=MINSVR;//银行当前提供服务的窗口数。3<=snum<=5。
int WINDOW[5];//记录每个窗口剩余服务时间，可取值0,1,2,3。

主要的算法思路：

for(clock=1;;clock++)在每个周期内
{
1.If客户等待队列非空
    将每个客户的等待时间增加一个时间单元

2.If(clock<=simulationtime)周期数小于等于有客户到来的周期数时
    从输入中读取本周期内新来的客户数，将其入队。
    根据等待客户数重新计算服务窗口数（对应刚才样例解释中的开始时等待人数）

3.If客户等待队列非空
    根据可用窗口数量，从等待队列中取出相应数目的客户（出队），并输出其等待时间。
    再根据等待客户数目重新计算服务窗口数（对应刚才样例解释中的结束时等待人数）。

4.如果客户等待队列空，且clock>simulationtime（不会再有新客户），结束模拟。
}

好我们现在开始看完整代码：

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define MAXSIZE 100
#define THRESHOLD 7//窗口增加阈值
#define MAXSVR 5//最大服务窗口数
#define MINSVR 3//最小服务窗口数
typedef struct
{
    int id;//客户排队号
    int wtime;//客户等待周期数
    int contact;//业务类型
}CustType;
CustType Cqueue[100];//等待服务的客户队列，一个循环队列
int Cfront=0;//队头
int Crear=MAXSIZE-1;//队尾
int Cnum=0;//队中元素个数
int isEmpty(){return Cnum==0;};
int isFull(){return Cnum==MAXSIZE;};

int Winnum=MINSVR;//银行当前提供服务的窗口数。3<=snum<=5。
int WINDOW[5]={0};//记录每个窗口剩余服务时间，可取值0,1,2,3。

void updateCustqueue();//更新等待队列中客户等待时间
void enCustqueue(CustType c);//客户入等待队列
CustType deCustqueue();//客户出队，同时输出其等待时间
void arriveCust(int);//获取新客户，并加入等待队列
int service();//从队列中获取客户进行服务

int main()
{
    int clock,simulationtime;
    scanf("%d",&simulationtime);
    
    int* each_period_num=(int*)malloc(sizeof(int)*simulationtime);
    for(int i=0;i<simulationtime;i++)
    {
        scanf("%d",&each_period_num[i]);
    }

    for(int clock=1;;clock++)
    {
        updateCustqueue();
        if(clock<=simulationtime)
            arriveCust(each_period_num[clock-1]);
        if(service()==0&&clock>simulationtime)
            break;
    }
    return 0;
}
void arriveCust(int n)
{
    int i,type;
    static int count=1;
    CustType c;
    for(int i=0;i<n;i++)
    {
        c.id=count;
        count++;
        c.wtime=0;
        scanf("%d",&c.contact);
        enCustqueue(c);
    }

    while((Cnum/Winnum)>=THRESHOLD&&Winnum<MAXSVR)
        Winnum++;
}
void enCustqueue(CustType c)
{
    if(isFull())
    {
        printf("full");
        exit(1);
    }
    Crear=(Crear+1)%MAXSIZE;
    Cqueue[Crear]=c;
    Cnum++;
}
CustType deCustqueue()
{
    CustType c;
    if(isEmpty())
    {
        printf("empty");
        exit(1);
    }
    c=Cqueue[Cfront];
    Cfront=(Cfront+1)%MAXSIZE;
    Cnum--;
    return c;
}
void updateCustqueue()
{
    int i;
    for(i=0;i<Cnum;i++)
        Cqueue[(Cfront+i)%MAXSIZE].wtime++;
    int j;
    for(j=0;j<Winnum;j++)
    {
        if(WINDOW[j]>0)
            WINDOW[j]--;
    }
}
int service()
{
    int i;
    CustType c;
    for(int i=0;i<Winnum;i++)
    {
        if(isEmpty())
            return 0;
        else 
        {
            int j=0;
            for(;j<Winnum;j++)
            {
                if(WINDOW[j]==0)
                    break;
            }
            if(j<Winnum)
            {c=deCustqueue();
            WINDOW[j]=c.contact;
            printf("%d : %d\n",c.id,c.wtime);}
        }
    }
    while((Cnum/Winnum)<THRESHOLD&&Winnum>MINSVR)
        Winnum--;
    return 1;
}