数据结构下的线性回归模型

news2024/11/18 11:41:55

文章目录

1. 线性回归模型的基本概念与原理
2. 数据结构在构建线性回归模型中的应用
- 2.1 数组和矩阵
- 2.2 列表
- 2.3 字典
- 2.4 数据框架
3. 线性回归模型的实现方法
4. 示例代码演示
总结

线性回归是统计学中最基础也是应用最广泛的预测模型之一，主要用于分析两个或两个以上变量间相互依赖的定量关系。在数据结构中，线性回归模型通常通过特征向量和相应的目标值向量来表示。

1. 线性回归模型的基本概念与原理

线性回归模型假设特征向量与目标值之间存在一个线性关系，可以用以下公式表示：
在这里插入图片描述

y 是目标值（或称为因变量）
X1 ,X2 ,…,Xn是特征向量中的特征值
β0，β1，…，βn，是线性模型的参数，也称为回归系数
ϵ 是误差项，表示模型未能解释的随机变异

2. 数据结构在构建线性回归模型中的应用

在构建线性回归模型时，适当的数据结构可以提高计算效率和代码的可维护性。以下是一些常用的数据结构及其在线性回归模型中的应用：

2.1 数组和矩阵

数组和矩阵是线性代数中的基础数据结构，可用于存储自变量和因变量的数据。例如，在多元线性回归中，自变量可以表示为矩阵，因变量可以表示为向量。

2.2 列表

列表（List）可以动态存储数据点，适用于数据集大小不固定的情况。列表还提供了便捷的访问和修改功能。

2.3 字典

字典（Dictionary）可以用于存储特征名称及其对应的数值，适用于需要快速查找和更新特征值的场景。

2.4 数据框架

数据框架（DataFrame）是用于数据处理和分析的高级数据结构，提供了灵活的数据操作和统计计算功能。在C#中，可以使用诸如DataTable或第三方库（如LINQ to DataSet）来实现类似的数据框架功能。

3. 线性回归模型的实现方法

首先，我们需要准备一个数据集，包括自变量和因变量。我们将使用数组来存储数据。
线性回归模型的训练主要是通过最小化误差平方和来估计回归系数。具体来说，我们需要找到一组 β 值，使得模型预测值与实际值之间的差异（即误差）的平方和最小。这可以通过以下公式表示：
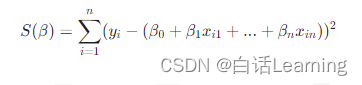
在这里插入图片描述
为了找到使 S(β) 最小的 β 值，我们可以使用梯度下降算法、牛顿法等优化算法。在这里，我们将使用梯度下降算法来进行模型训练。

4. 示例代码演示

下面是一个详细的C#示例，展示了如何实现一个线性回归模型：

using System;
using System.Collections.Generic;

public class LinearRegression
{
    private List<double[]> dataPoints;
    private double beta0, beta1;

    public LinearRegression(List<double[]> dataPoints)
    {
        this.dataPoints = dataPoints;
        beta0 = beta1 = 0;
        Train();
    }

    private void Train()
    {
        int n = dataPoints.Count;
        double sumX = 0, sumY = 0, sumXY = 0, sumXX = 0;

        foreach (var point in dataPoints)
        {
            sumX += point[0];
            sumY += point[1];
            sumXY += point[0] * point[1];
            sumXX += point[0] * point[0];
        }

        beta1 = (n * sumXY - sumX * sumY) / (n * sumXX - sumX * sumX);
        beta0 = (sumY - beta1 * sumX) / n;
    }

    public double Predict(double x)
    {
        return beta0 + beta1 * x;
    }
}

public class Program
{
    public static void Main()
    {
        List<double[]> dataPoints = new List<double[]>
        {
            new double[] {1, 1},
            new double[] {2, 2},
            new double[] {3, 3},
            new double[] {4, 4}
        };

        var model = new LinearRegression(dataPoints);

        Console.WriteLine("Prediction for x = 5: " + model.Predict(5));
    }
}