leetcode 链接:
所有可能的路径
1 图的基本概念
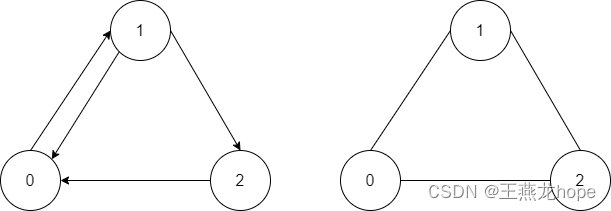
1.1 有向图和无向图
左边是有向图,右边是无向图。对于无向图来说,图中的边没有方向,两个节点之间只可能存在一条边,比如 0 和 1 之间的边,因为是无向图,这条边可以表示从 0 到 1 的边,也可以表示从 1 到 0 的边。对于有向图来说,图中的边有方向, 0 和 1 之间可以存在两条边,一条表示从 0 到 1 的边,一条表示从 1 到 0 的边。
用邻接矩阵来表示上边两个图,如下所示。
// 有向图
[
[1], // 有从 0 到 1 的边
[0, 2], // 从 1 到 0 的边和从 1 到 2 的边
[0] // 从 2 到 0 的边
]
// 无向图
[
[1, 2], // 从 0 到 1 和从 0 到 2 的边
[0, 2], // 从 1 到 0 和从 1 到 2 的边
[0, 1] // 从 2 到 0 和从 2 到 1 的边
]1.2 有环图和无环图
讨论有环图还是无环图,一般说的是有向图。因为对于无向图来说,从 0 到 1 有边,那么从 1 到 0 就有边,本身就是一个环。
有环图说的是从一个节点开始遍历,在遍历过程中还能遍历到这个节点的图,除了开始节点和结束节点是相同的,其它节点不能重复出现,并且路径长度大于 2。
在图的遍历算法中,为了防止一个节点被重复遍历,往往需要一个 visited[n] 数组来标记一个节点是不是被遍历过。visited 数组下标是节点的值,元素值均被初始化为 0,当一个节点被遍历时,则将值改为 1。对于有向有环图来说,需要 visited 数组来标记,因为有环,一个节点可能被多次访问;对于有向无环图来说,一个节点不会被重复遍历,所以不需要 visited 数组来标记。
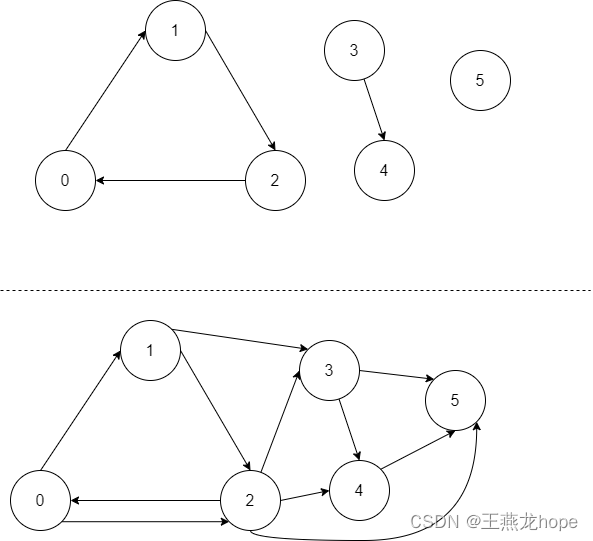
1.3 连通图和非连通图
下边两个图,上边的是非连通图,下边的是连通图。连通图,指的是从一个节点出发沿着边进行遍历,能把图中的节点都遍历到的图。 这个很像那种益智小游戏,看怎么样能一笔把图中的所有点连起来。
当对图做遍历时,如果图是连通的,那么从一个节点开始,遍历一次,就能将图中所有的节点遍历一遍,所以遍历一次就可以了。如果图不是连通的,那么遍历一次,无法将所有的点都遍历一遍,这个时候要从每个点都开始,每个节点都要开始一次,遍历一遍。
2 深度优先搜索和广度优先搜索
图是一种二维的数据结构,可以使用邻接表或者邻接矩阵来表示,更多的使用邻接表来表示,有行和列。
1.3 节中连通图的邻接矩阵表示如下:
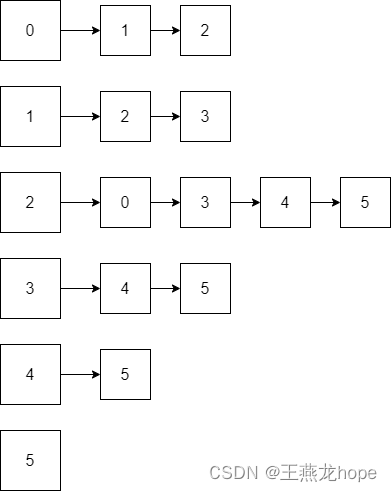
深度优先,从遍历过程来看,优先在纵向遍历,纵深,深度。
广度优先,从遍历过程来看,优先在横向遍历,横向是广度。
纵向是深度,横向是广度。
上边这个图,从节点 0 开始遍历,第一步遍历到节点 1,下一步遍历的选择就是深度优先和广度优先的区别。下一步遍历 1 节点开始的链表,也就是跳到第二行开始遍历,遍历到节点 1 的邻接点 2,这就是深度优先遍历;下一步还是在 0 这一行,遍历节点 2,这就是广度优先遍历。
深度优先遍历和广度优先遍历不仅仅适用于图这种数据结构。二叉树的遍历包括前序遍历,中序遍历,后序遍历以及层序遍历。前 3 种遍历方式属于深度优先遍历,层序遍历属于广度优先遍历。二叉树也属于二维的数据结构。
二叉树遍历算法和应用
2.1 时间复杂度
深度优先和广度优先遍历图,都是沿着边进行遍历的。如果节点个数是 n,那么对于无向图来说,边的个数最大是 n(n - 1)/2;对有向图来说,边的个数最大是 n(n - 1)。
所以最差的情况下,两种算法的时间复杂度均是 O(n * n)。
3 所有可能的路径
如下是 leetcode 中的题目说明。
题意中的图是有向无环图,有向并且没有环,所以在遍历的时候不需要使用 visited 数据来标记一个节点是不是被访问过,因为没有环,一个节点不会被重复访问。

3.1 深度优先
这个题目适合使用深度优先遍历算法。深度优先遍历,是递归算法,递归算法需要注意两点:递归退出条件,一定要有退出条件,否则会一直递归下去;递归体,也就是递归算法的主要逻辑。递归算法的这两点与循环类似,循环算法也包括循环退出条件和循环主要逻辑。
找路径的题目,使用递归算法的题目,不管是图和是二叉树,最核心的就是如下代码注释中的三段式。
(1)将节点加入到路径
(2)递归
(3)将节点移出路径
为什么加入的节点要移出呢,因为这个节点加入之后,进行了递归运算。也就是说以这个节点为基础的路径都已经全部遍历。下一次要遍历的节点与这个节点是并列的节点,并不是路径的前后关系,它们属于这一行的邻接点。要进行下一步遍历,这个节点需要移出,因为后边遍历的节点跟这个节点不在一个路径,只不过都是当前这一行的得邻接点而已。
class Solution {
public:
vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
const int n = graph.size();
// 没有数据,直接返回
if (n == 0) {
return ret;
}
// 要找的路径是从 o 到 n - 1
// 所以从 0 开始遍历
// 在遍历之前要把这个点加入到路径中
one_path.push_back(0);
// 深度优先遍历
DfsScan(graph, 0, n);
return ret;
}
// 深度优先遍历时一种递归算法
void DfsScan(vector<vector<int>>& graph, int index, const int n) {
// 递归退出条件,当前这个点是 n - 1 的时候,说明找到了这样一个路径
// 将这条路径加入到结果中
if (index == n - 1) {
ret.push_back(one_path);
return;
}
// 递归体,深度优先搜索
// 对于遍历的这个节点,找到这个节点锁代表的这一行,遍历这一行
// 这种方式取出数据的一行,会发生拷贝,直接使用引用来获取数据可以避免数据拷贝
// vector<int> line = graph[index];
// int line_size = line.size();
// for (int i = 0; i < line_size; i++) {
for (int & data : graph[index]) {
// 三段式
// 1、push_back 将节点加入到路径中
// 2、递归运算
// 3、将节点从路径中移走
one_path.push_back(data);
DfsScan(graph, data, n);
one_path.pop_back();
}
}
private:
vector<vector<int>> ret;
vector<int> one_path;
};3.2 广度优先
广度优先需要使用一个队列和循环算法。在循环之前将一个元素加入到队列中,循环的条件是队列不为空,循环中的逻辑是把新遍历到的节点加入到队列中。
找路径这样的题目,广度优先没有深度优先好理解。深度优先在遍历的过程中,前后相邻的两个被遍历的点一定是一条路径上的前后的两个点,这样遍历到一个点,直接追加到路径上就可以。而广度优先遍历不是这样的,相邻两次遍历的点不是属于路径上的前后点,而是只属于当前这一行首节点的邻接点。这样就需要给每个节点维护一个路径,当这个节点是首节点的时候,那么这个节点的所有邻接点的路径都要更新,都要在这个首节点的路径的基础上加上当前这个节点。
class Solution {
public:
struct Node {
int data;
vector<int> path;
};
vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
int size = graph.size();
if (size == 0) {
return ret;
}
Node node;
node.data = 0;
// 将节点加入到队列中
// 节点保存着到当前这个节点的路径
node.path.push_back(0);
// 循环的出发条件,只要队列不是空,循环就继续进行
q.push(node);
while (!q.empty()) {
// 从队列中获取一个元素
// 开始遍历以这个元素为行首的节点,即广度优先遍历
Node tmp = q.front();
q.pop();
for (int &d : graph[tmp.data]) {
Node linenode;
linenode.data = d;
linenode.path = tmp.path;
linenode.path.push_back(d);
// 当前这个节点是 size - 1 了,找到了满足条件的一个路径
// 那么这个节点就不需要加入队列了
// 加入队列之后下次遍历的时候,路径后边还要加入其它节点
// 继续追加没有意义,因为当前已经是要找的路径了
if (d == size - 1) {
ret.push_back(linenode.path);
} else {
q.push(linenode);
}
}
}
return ret;
}
private:
std::queue<Node> q;
vector<vector<int>> ret;
};