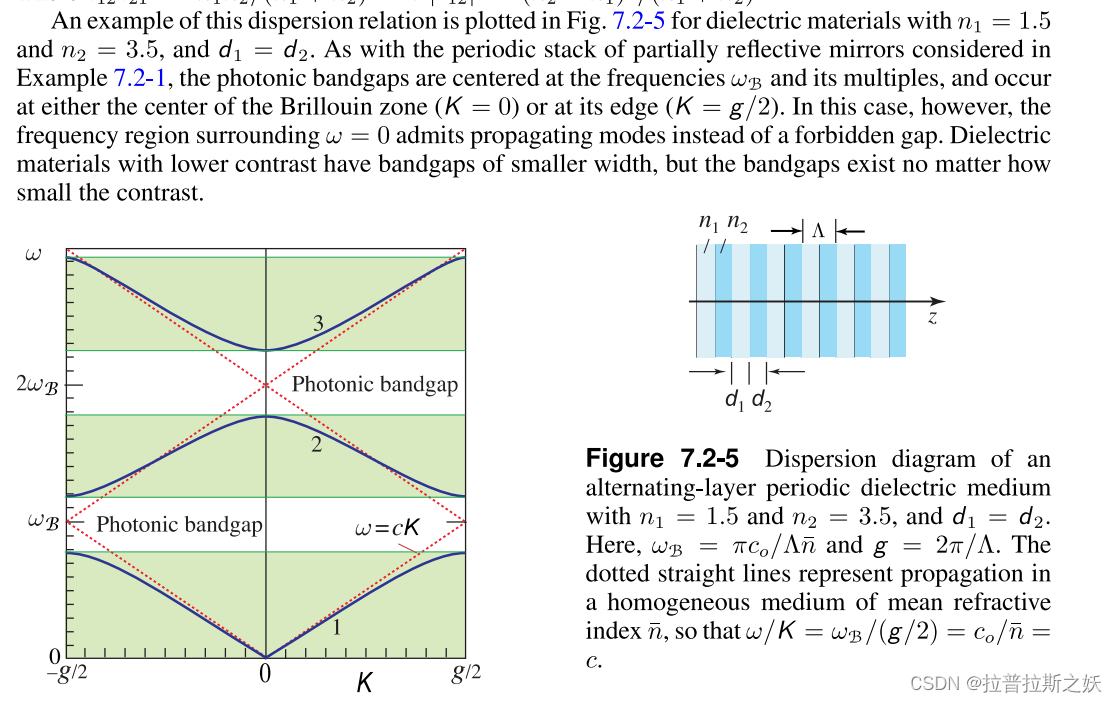
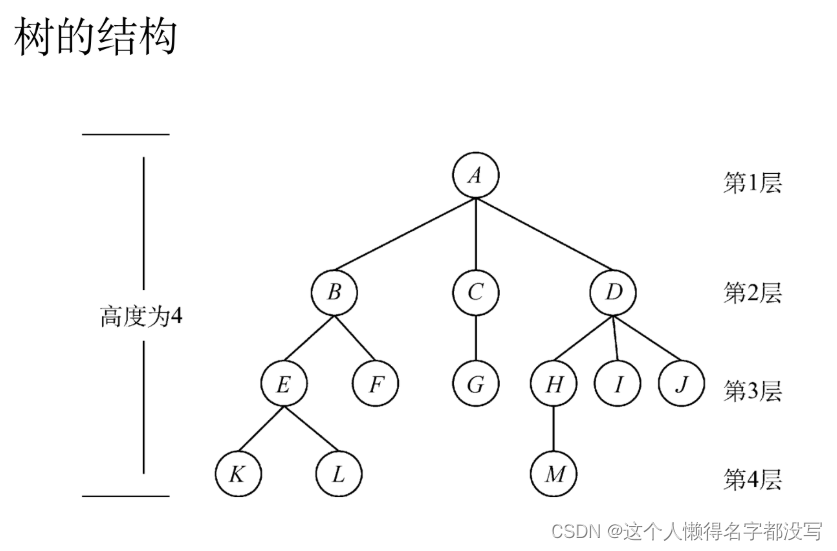
树二叉树

news2025/1/13 3:36:00

树

​ 树是 n（n≥0）个结点的有限集。当 n = 0时，称为空树。在任意一颗非空树中应满足：

（1）有且仅有一个特定的称为根的结点。

（2）当 n > 1时，其余结点可分为 m（m > 0）个互不相交的有限集T1, T2, …, Tm，其中每个集合本身又是一棵树，并且称为根的子树。

​ 树作为一种逻辑结构，同时也是一种分层结构，具有以下两个特点：

（1）树的根结点没有前驱，除根结点外的所有结点有且只有一个前驱。

（2）树中所有结点可以有零个或多个后继。
请添加图片描述

二叉树

​ 二叉树是另一种树形结构，其特点是每个结点至多只有两颗字数（即二叉树中不存在度大于2的结点），并且二叉树的子树有左右之分，其次序不能任意颠倒。

​ 与树相似，二叉树也以递归的形式定义，二叉树是 n（n ≥ 0）个结点的有限集合：

（1）或者为空二叉树，即 n = 0。

（2）或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树分别是一颗二叉树。

满二叉树：

如果一棵二叉树只有度为0的节点和度为2的节点，并且度为0的节点在同一层上，则这棵二叉树为满二叉树 。
1
2
3
4
5
6
7

完全二叉树：

深度为k，有n个节点的二叉树当且仅当其每一个节点都与深度为k的满二叉树中编号从1到n的节点一一对应时，称为完全二叉树。
1
2
3
4
5
6

普通二叉树：
1
2
3
4
5
6
7
8
9
10
A
B
D
C

二叉查找树：

二叉查找树又称二叉排序树或者二叉搜索树。
1
2
3
4
5
6
7
8
9
10
A
B
D
C

特点：

  • 每个节点上最多有两个子节点。
  • 左子树上所有节点的值都小于根节点的值。
  • 右子树上所有节点的值都大于根节点的值。

目的：

  • 提高检索数据的性能。

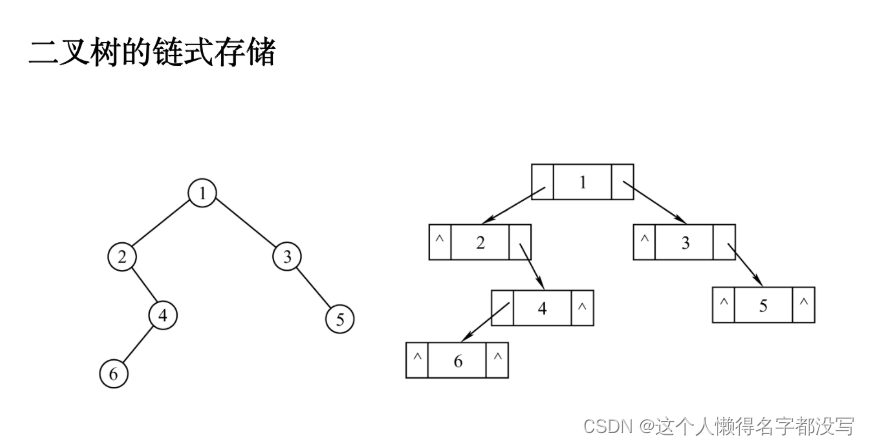
二茶树的链式存储

typedef char BiElemType;
typedef struct BiTNode {
    BiElemType data;
    struct BiTNode *lchild;
    struct BiTNode *rchild;
}

请添加图片描述

二叉树建树

#include <stdio.h>
#include <stdlib.h>


typedef char BiElemType;
// 树结点
typedef struct BiTNode {
    // 数据
    BiElemType data;
    // 左子树
    struct BiTNode *lchild;
    // 右子树
    struct BiTNode *rchild;

} BiTNode, *BiTree;

// 用于构建辅助链队结点
typedef struct LinkNode {
    // 用于存储树的某一个结点的地址
    BiTree p_tree;
    struct LinkNode *next;
} LinkNode;


int main() {

    // 创建树根
    BiTree Tree = NULL;

    // 用来指向新申请的树结点
    BiTree tree_new_node;

    // 队列头 队列尾 队列新结点 当前树的父结点（要插入结点的位置）
    LinkNode *q_head = NULL, *q_tail = NULL, *q_new_node = NULL, *q_cur = NULL;

    char c;
    while (scanf("%c", &c)) {
        if ('\n' == c) {
            break;
        }

        // 申请树结点
        // calloc 申请空间并对空间进行初始化为0
        tree_new_node = (BiTree) calloc(1, sizeof(BiTNode));
        tree_new_node->data = c;

        // 队列新结点
        q_new_node = (LinkNode *) calloc(1, sizeof(LinkNode));
        // 新结点p_tree存储新的树结点地址
        q_new_node->p_tree = tree_new_node;
        q_new_node->next = NULL;

        // 如果树为空
        if (NULL == Tree) {
            // 树根
            Tree = tree_new_node;

            // 队首
            q_head = q_new_node;
            // 队尾
            q_tail = q_new_node;
            // 当前树的父结点（要插入结点的位置）
            q_cur = q_new_node;

            // 结束本次循环
            continue;
        } else {
            // 新结点放入队列中
            q_tail->next = q_new_node;
            // 新结点成为新尾部
            q_tail = q_new_node;
        }

        // 当前父结点插入左子树
        if (NULL == q_cur->p_tree->lchild) {
            q_cur->p_tree->lchild = tree_new_node;
        } else if (NULL == q_cur->p_tree->rchild) {
            q_cur->p_tree->rchild = tree_new_node;

            //当前父结点左右子树都有了 队列下一个结点作为树的父结点
            q_cur = q_cur->next;
        }
    }

    return 0;
}

二叉树遍历

深度优先遍历

二叉树的深度优先遍历有三种方式，前序遍历、中序遍历、后序遍历。

  • 前序遍历是先打印自身，再打印左子树，再打印右子树。
  • 中序遍历是先打印左子树，再打印自身，再打印右子树，中序遍历相当于把树压扁。
  • 后序遍历是先打印左子树，再打印右子树，最后打印当前结点。
#include <stdio.h>
#include <stdlib.h>


typedef char BiElemType;
// 树结点
typedef struct BiTNode {
    // 数据
    BiElemType data;
    // 左子树
    struct BiTNode *lchild;
    // 右子树
    struct BiTNode *rchild;

} BiTNode, *BiTree;

// 用于构建辅助链队结点
typedef struct LinkNode {
    // 用于存储树的某一个结点的地址
    BiTree p_tree;
    struct LinkNode *next;
} LinkNode;


/*
 * 先序遍历
 * 用递归思想解决 把每个结点看作一棵树
 */
void pre_order(BiTree p) {
    if (NULL != p) {
        // 本身
        printf("%c", p->data);
        // 左子树
        pre_order(p->lchild);
        // 右子树
        pre_order(p->rchild);
    }
}

/*
 * 中序遍历
 * 用递归思想解决 把每个结点看作一棵树
 */
void in_order(BiTree p) {
    if (NULL != p) {
        // 左子树
        in_order(p->lchild);
        // 本身
        printf("%c", p->data);
        // 右子树
        in_order(p->rchild);
    }
}


/*
 * 后续遍历
 * 用递归思想解决 把每个结点看作一棵树
 */
void post_order(BiTree p) {
    if (NULL != p) {
        // 左子树
        post_order(p->lchild);
        // 右子树
        post_order(p->rchild);
        // 本身
        printf("%c", p->data);
    }
}


int main() {

    // 创建树根
    BiTree Tree = NULL;

    // 用来指向新申请的树结点
    BiTree tree_new_node;

    // 队列头 队列尾 队列新结点 当前树的父结点（要插入结点的位置）
    LinkNode *q_head = NULL, *q_tail = NULL, *q_new_node = NULL, *q_cur = NULL;

    char c;
    while (scanf("%c", &c)) {
        if ('\n' == c) {
            break;
        }

        // 申请树结点
        // calloc 申请空间并对空间进行初始化为0
        tree_new_node = (BiTree) calloc(1, sizeof(BiTNode));
        tree_new_node->data = c;

        // 队列新结点
        q_new_node = (LinkNode *) calloc(1, sizeof(LinkNode));
        // 新结点p_tree存储新的树结点地址
        q_new_node->p_tree = tree_new_node;
        q_new_node->next = NULL;

        // 如果树为空
        if (NULL == Tree) {
            // 树根
            Tree = tree_new_node;

            // 队首
            q_head = q_new_node;
            // 队尾
            q_tail = q_new_node;
            // 当前树的父结点（要插入结点的位置）
            q_cur = q_new_node;

            // 结束本次循环
            continue;
        } else {
            // 新结点放入队列中
            q_tail->next = q_new_node;
            // 新结点成为新尾部
            q_tail = q_new_node;
        }

        // 当前父结点插入左子树
        if (NULL == q_cur->p_tree->lchild) {
            q_cur->p_tree->lchild = tree_new_node;
        } else if (NULL == q_cur->p_tree->rchild) {
            q_cur->p_tree->rchild = tree_new_node;

            //当前父结点左右子树都有了 队列下一个结点作为树的父结点
            q_cur = q_cur->next;
        }
    }

    // 先序遍历
    printf("Pre Order: ");
    pre_order(Tree);
    printf("\n");

    // 中序遍历
    printf("In Order: ");
    in_order(Tree);
    printf("\n");

    // 后序遍历
    printf("Post Order: ");
    post_order(Tree);
    printf("\n");

    return 0;
}

输入结果：

abcdefghi
Pre Order: abdhiecfg
In Order: hdibeafcg
Post Order: hidebfgca

Process finished with exit code 0

广度优先遍历

​ 层次遍历是一种广度优先遍历，层次遍历与层次建树的原理非常相似。层次遍历必须试用辅助队列。

#include <stdio.h>
#include <stdlib.h>


typedef char BiElemType;
// 树结点
typedef struct BiTNode {
    // 数据
    BiElemType data;
    // 左子树
    struct BiTNode *lchild;
    // 右子树
    struct BiTNode *rchild;

} BiTNode, *BiTree;

// 用于构建辅助链队结点
typedef BiTNode ElemType;
typedef struct LinkNode {
    ElemType *data;
    struct LinkNode *next;
} LinkNode;
typedef struct LinkQueue {
    LinkNode *front, *rear;
} LinkQueue;


/*
 * 队列初始化
 */
void init_queue(LinkQueue &Q) {
    Q.front = Q.rear = (LinkNode *) malloc(sizeof(LinkNode));
    Q.front->next = NULL;
}


/*
 * 队列是否为空
 */
bool queue_empty(LinkQueue Q) {
    return Q.front == Q.rear;
}


/*
 * 入队
 */
void enqueue(LinkQueue &Q, BiTree T) {
    LinkNode *s = (LinkNode *) malloc(sizeof(LinkNode));
    s->data = T;
    s->next = NULL;
    Q.rear->next = s;
    Q.rear = s;
}

/*
 * 出队
 */
bool dequeue(LinkQueue &Q, BiTree &T) {
    // 队列为空
    if (queue_empty(Q)) {
        return false;
    }

    LinkNode *p = Q.front->next;
    T = p->data;

    Q.front->next = p->next;
    if (Q.rear == p) {
        Q.rear = Q.front;
    }
    free(p);
    return true;
}


/*
 * 层序遍历
 *
 * 跟层次建树几乎一样 用辅助队列实现
 */
void level_order(BiTree T) {
    LinkQueue Q;
    init_queue(Q);

    // 树根入队
    enqueue(Q, T);
    // 从队列出队的树结点
    BiTree p;

    // 队列不为空
    while (!queue_empty(Q)) {
        // 出队
        dequeue(Q, p);
        putchar(p->data);

        // 判断当前结点是否有左孩子
        if (NULL != p->lchild) {
            // 左孩子入队
            enqueue(Q, p->lchild);
        }

        // 判断当前结点是否有右孩子
        if (NULL != p->rchild) {
            // 右孩子入队
            enqueue(Q, p->rchild);
        }
    }

}


int main() {

    // 创建树根
    BiTree Tree = NULL;

    // 用来指向新申请的树结点
    BiTree tree_new_node;

    // 队列头 队列尾 队列新结点 当前树的父结点（要插入结点的位置）
    LinkNode *q_head = NULL, *q_tail = NULL, *q_new_node = NULL, *q_cur = NULL;

    char c;
    while (scanf("%c", &c)) {
        if ('\n' == c) {
            break;
        }

        // 申请树结点
        // calloc 申请空间并对空间进行初始化为0
        tree_new_node = (BiTree) calloc(1, sizeof(BiTNode));
        tree_new_node->data = c;

        // 队列新结点
        q_new_node = (LinkNode *) calloc(1, sizeof(LinkNode));
        // 新结点p_tree存储新的树结点地址
        q_new_node->data = tree_new_node;
        q_new_node->next = NULL;

        // 如果树为空
        if (NULL == Tree) {
            // 树根
            Tree = tree_new_node;

            // 队首
            q_head = q_new_node;
            // 队尾
            q_tail = q_new_node;
            // 当前树的父结点（要插入结点的位置）
            q_cur = q_new_node;

            // 结束本次循环
            continue;
        } else {
            // 新结点放入队列中
            q_tail->next = q_new_node;
            // 新结点成为新尾部
            q_tail = q_new_node;
        }

        // 当前父结点插入左子树
        if (NULL == q_cur->data->lchild) {
            q_cur->data->lchild = tree_new_node;
        } else if (NULL == q_cur->data->rchild) {
            q_cur->data->rchild = tree_new_node;

            //当前父结点左右子树都有了 队列下一个结点作为树的父结点
            q_cur = q_cur->next;
        }
    }

    // 层次遍历
    printf("Level Order: ");
    level_order(Tree);

    return 0;
}

输出结果：

abcdefghi
Level Order: abcdefghi

Process finished with exit code 0

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1810946.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

管理的三大关键：定目标、抓过程、拿结果

管理的三大关键：定目标、抓过程、拿结果

第一板斧&#xff1a;定目标 想清楚&#xff0c;写清楚&#xff0c;讲清楚&#xff0c;才能干明白 没有见过伟大&#xff0c;谈何伟大&#xff1f;很多管理者之所以定不好目标&#xff0c;是因为他们根本不知道也没见过好目标是什么样的&#xff0c;谈何定出好目标&#xff…
阅读更多...
无源晶振振荡电路失效问题分析与解决策略

无源晶振振荡电路失效问题分析与解决策略

无源晶振&#xff08;晶体谐振器&#xff09;在电子设备中扮演着至关重要的角色&#xff0c;为数字电路提供稳定的时钟信号。然而&#xff0c;振荡电路一旦失效&#xff0c;可能会导致整个系统运行不正常。晶发电子将从三个主要方面分析无源晶振振荡电路失效的问题&#xff0c;…
阅读更多...
测试开发面经分享，面试七天速成

测试开发面经分享，面试七天速成

1. get、post、put、delete的区别 a. get请求&#xff1a; i. 用于从服务器获取资源。请求参数附加在URL的查询字符串中。 ii. 对服务器的请求是幂等的&#xff0c;即多次相同的GET请求应该返回相同的结果。 iii. 可以被缓存&#xff0c;可以被收藏为书签。 iv. 对于敏感数据不…
阅读更多...
【回调函数】

【回调函数】

1.回调函数是什么&#xff1f; 回调函数就是⼀个通过函数指针调用的函数。 如果你把函数的指针&#xff08;地址&#xff09;作为参数传递给另⼀个函数&#xff0c;当这个指针被用来调用其所指向的函数 时&#xff0c;被调用的函数就是回调函数。回调函数不是由该函数的实现方…
阅读更多...
MySQL—多表查询—小结

MySQL—多表查询—小结

一、引言 前面的博客已经全部学习完了关于多表查询。接下来对多表查询进行一个小结。 &#xff08;1&#xff09;多表查询主要是讲了两个方面 多表关系 &#xff08;不管业务关系如何的复杂&#xff0c;最终多表的关系基本上可以分为三类&#xff09; "一对多"、&qu…
阅读更多...
每天一个数据分析题（三百五十九）- 多维分析模型

每天一个数据分析题（三百五十九）- 多维分析模型

图中是某公司记录销售情况相关的表建立好的多维分析模型&#xff0c;请根据模型回答以下问题&#xff1a; 2&#xff09;产品表左连接品牌表的对应关系属于&#xff1f; A. 一对多 B. 一对一 C. 多对一 D. 多对多 数据分析认证考试介绍&#xff1a;点击进入 题目来源于CD…
阅读更多...
拯救学弟学妹计划之【论文帮手】是如何实现的？

拯救学弟学妹计划之【论文帮手】是如何实现的？

功能介绍 概述 论文帮手是一款专为学术研究者设计的智能应用&#xff0c;旨在提供论文撰写和研究支持。应用通过深入了解用户的研究领域和需求&#xff0c;利用先进的搜索技术和人工智能&#xff0c;为用户提供定制化的学术资源和写作支持。 功能详述 1. 相关论文查找 此功…
阅读更多...
Androidstudio项目加载不出来,显示Connect timed out

Androidstudio项目加载不出来,显示Connect timed out

Android studio加载不出来所需要的环境依赖,99%的问题都是网络原因 解决办法有两个: 1.科学上网 2.使用国内的镜像 方法一自行解决,下面重点介绍方法二 在项目目录下找到gradle->wrapper->gradle-wrapper.properties 将项目的distributionUrl改为https://mirrors.cl…
阅读更多...
SwiftUI七使用UI控件

SwiftUI七使用UI控件

代码下载 在应用中&#xff0c;用户可以创建一个简介来描述他们自已的个人情况。为了让用户可以编辑自己的简介&#xff0c;需要添加一个编辑模式并设计一个偏好设置界面。这里使用多种通用控件来展示用户的各种数据&#xff0c;并在用户保存他们所做的数据修改时更新地标数据…
阅读更多...
【物料选型】东芝（Toshiba）车载器件选型和应用

【物料选型】东芝（Toshiba）车载器件选型和应用

东芝&#xff08;Toshiba&#xff09;拥有汽车电气化所需的丰富的半导体产品&#xff0c;专注于用于电动助力转向、电动水泵和电动空调风扇等应用的车载逆变器、电池管理系统和电机驱动。特别是高压和低损耗功率器件的表现优异。未来&#xff0c;东芝将继续提供面向未来的尖端半…
阅读更多...
自动驾驶TPM技术杂谈 ———— 车用温度传感器

自动驾驶TPM技术杂谈 ———— 车用温度传感器

文章目录 介绍描述冷却液温度传感器进气温度传感器变速器油温传感器排气温度传感器EGR废气循环监测温度传感器车外温度传感器车内温度传感器日照温度传感器空调蒸发器出口温度传感器热敏铁氧体温度传感器 介绍 温度传感器是一种常见的传感器类型&#xff0c;广泛应用于温度检测…
阅读更多...
Objective-C 学习笔记 | 回调

Objective-C 学习笔记 | 回调

Objective-C 学习笔记 | 回调 Objective-C 学习笔记 | 回调运行循环目标-动作对&#xff08;target-action&#xff09;辅助对象通知回调与对象所有权深入学习&#xff1a;选择器的工作机制 参考书&#xff1a;《Objective-C 编程&#xff08;第2版&#xff09;》 Objective-C…
阅读更多...
git服务器gitblit安装

git服务器gitblit安装

1、下载 Gitblit 2、下载完后解压&#xff1a; 3、配制&#xff1a; 保存&#xff0c;退出编辑。 4、运行cmd&#xff0c;启用gitblit。 5、根据运行后的提示&#xff0c;也就是我们之间设置的port9990打开&#xff1a; 输入admin,admin就可以登录&#xff0c;这个账号密码&a…
阅读更多...
LaTex中`\texorpdfstring`命令的使用方法

LaTex中`\texorpdfstring`命令的使用方法

LaTex中\texorpdfstring命令的使用方法 \texorpdfstring命令 \texorpdfstring命令是hyperref包提供的一种替换宏&#xff0c;常用于标题中的公式显示。 命令后跟随两个参数&#xff1a; \texorpdfstring{TeXstring}{PDFstring}第一个参数TeXstring在正文标题中显示&#xf…
阅读更多...
MySQL存储引擎详述：InnoDB为何胜出？

MySQL存储引擎详述：InnoDB为何胜出？

MySQL作为当前最流行的开源关系型数据库之一,其强大的功能和良好的性能使其广泛应用于各种规模的应用系统中。其中,存储引擎的设计理念是MySQL数据库灵活高效的关键所在。 一、什么是存储引擎 存储引擎是MySQL架构的重要组成部分,负责MySQL中数据的存储和提供了视图,存储过程等…
阅读更多...
半导体光电子学最后总结（3）光子晶体

半导体光电子学最后总结（3）光子晶体

Matrix theory 波传输矩阵 (Wave-Transfer Matrix) 散射矩阵 (Scattering Matrix) 光在均匀介质中的传播公式矩阵化 Relation between Scattering Matrix and Wave-Transfer Matrix 级联系统的投射/反射系数&#xff1a;艾里公式 (Airy Formulas) 无损对称系统 斜入射波的传输…
阅读更多...
Golang的context

Golang的context

目录 context的基本使用 为什么需要context Context interface 标准 error emptyCtx cancelCtx Deadline 方法 Done 方法 Err 方法 Value 方法 context.WithCancel() newCancelCtx WithCancel中propagateCancel cancel timerCtx valueCtx context的基本使用…
阅读更多...
宽睿数字平台兼容TDengine 等多种数据库，提供行情解决方案

宽睿数字平台兼容TDengine 等多种数据库，提供行情解决方案

小T导读&#xff1a;最近&#xff0c;涛思数据与宽睿金融宣布了一项重要合作。在此之前&#xff0c;宽睿金融对 TDengine 进行了性能测试&#xff0c;并根据测试报告的结果&#xff0c;决定将 TDengine 接入宽睿数字平台&#xff0c;以提升高密度行情处理效率。本文将详细介绍此…
阅读更多...
智慧监狱大数据整体解决方案（51页PPT）

智慧监狱大数据整体解决方案（51页PPT）

方案介绍&#xff1a; 智慧监狱大数据整体解决方案通过集成先进的信息技术和大数据技术&#xff0c;实现对监狱管理的全面升级和智能化改造。该方案不仅提高了监狱管理的安全性和效率&#xff0c;还提升了监狱的智能化水平&#xff0c;为监狱的可持续发展提供了有力支持。 部…
阅读更多...
【Vue】获取模块内的actions方法

【Vue】获取模块内的actions方法

目标&#xff1a; 掌握模块中 action 的调用语法 (同理 - 直接类比 mutation 即可) 注意&#xff1a; 默认模块中的 mutation 和 actions 会被挂载到全局&#xff0c;需要开启命名空间&#xff0c;才会挂载到子模块。 调用语法&#xff1a; 直接通过 store 调用 $store.di…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023