[机器学习]损失函数DLC

news2025/1/9 1:59:13

一、损失函数的概念

损失函数(Loss Function)是用于评估预测结果 $\hat{y}$ 和真实结果 $y$ 之间差距的一个公式，为模型优化指明方向。在模型优化过程中一般表述为： $L(y_i,f(x_i;\theta))$ 或 $L(y_i,\hat{y_i})$

与针对整个训练集的代价函数(Cost Function)不同，损失函数通常仅针对单个训练样本。可以归纳为A loss function is a part of a cost function。(损失函数是代价函数的一部分)

二、常见的损失函数及其详解

1.均方差损失

均方差(Mean Squared Error,MSE)损失函数一般用于回归任务，也称L2 Loss

$J_{MSE}=\frac{1}{N}\sum(y_i-\hat{y_i})^2$

在使用均方差损失函数时，可以视为模型输出和真实值之间的误差服从高斯分布

2.平均绝对误差损失

平均绝对误差（Mean Absolute Error Loss，MAE），又称L1 Loss

$J_{MAE}=\frac{1}{N}\sum|y_i-\hat{y_i}|$

在使用平均绝对误差损失函数时，可以视为模型输出和真实值之间的误差服从拉普拉斯分布

3.HUber Loss

又称Smooth L1 Loss，L1 Loss在0点导数不唯一，可能会影响收敛；而Smooth L1 Loss在0点附近使用平方函数使其变得更为平滑

$Smooth L_1 = 0.5x^2,|x|<1$

$=|x|-0.5, x<-1||x>1$

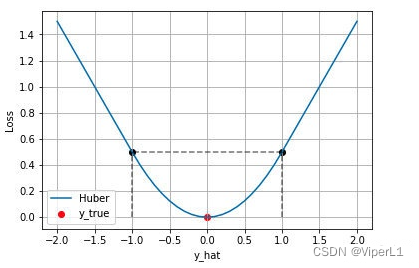
MAE和MSE的区别

①L2 Loss的收敛速度快于L1 Loss，一般使用L2 Loss的情况居多

②L1 Loss的增长比较缓慢(随误差线性增长，而不是平方增长)，即对异常值(outlier)不敏感；对于边框预测回归问题(如Faster RCNN)而言，其梯度变化更小，更不易跑飞

4.交叉熵损失函数

Cross Entropy Loss，一般应用于分类问题，可分为二分类和多分类

4.1二分类

对于二分类而言，我们通常用sigmoid函数将模型压缩至(0,1)，模型输出结果为概率，对于给定的输入 $x_i$ ，其为正例和为负例的概率分别为：

$p(y_i=1|x_i)=\hat{y_i}$

$p(y_i=0|x_i)=1-\hat{y_i}$

将这两个式子合并可得： $p(y_i|x_i)=(\hat{y_i})^{y_i}(1-\hat{y_i})^{1-y_i}$

假定数据点之间互相独立，其似然分布可表述为： $L(x,y)=\prod (\hat{y_i}^{y_i})(1-\hat{y_i})^{1-\hat{y_i}}$

取似然对数并加负号变为最小化负对数似然，即可得到交叉损失函数的形式

$J_{CE}=-\sum y_i log(\hat{y_i})+(1-y_i)log(1-\hat{y_i})$

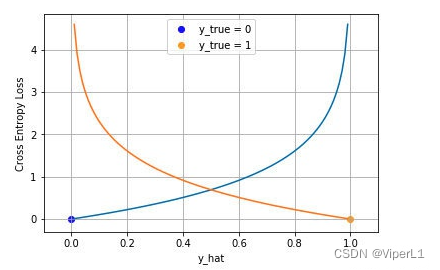
4.2多分类

多分类思想类似于二分类，真实值 $y_i$ 为一个One-hot向量；用来压缩的函数改为softmax，所有维度的输出范围被压缩为(0,1)，且其和为1，可以表述为： $p(y_i|x_i)=\prod (\hat{y}^k_i)^{y_i^k}$

取似然对数并加负号变为最小化负对数似然，即可得到交叉损失函数的形式

$J_{CE}=-\sum y_i^{c_i}log(y_i^{\hat{(c_i)}})$

4.3Focal Loss

Focal Loss基于交叉熵损失函数，用于解决传统交叉熵损失函数中以下问题：

①负样本(Negative example)过多导致正样本(Postive example)的Loss被覆盖

②简单样本(Easy example)过多导致其支配某个批次的收敛方向

Focal Loss可以表述为：

$FL(p_t)=-\alpha_t(1-p_t)^\gamma log(p_t)$

其中 $\alpha_t$ 和γ分别用于解决正负样本不平衡问题和难易样本不平衡问题

以二分类为例，将其展开

$p_t=p,y=1$

$=1-p,otherwise$

4.3.1 α

用于解决正负样本不平衡问题；为正负样本分类不同的权重值α [0,1]

$\alpha_t=\alpha,y=1$

$=1-\alpha,otherwise$

α的值往往需要根据结论进行调整(Faster RCNN论文中为0.25)

4.3.2 γ

用于解决难易样本不平衡问题；让每个样本乘以 $(1-p_t)^\gamma$ ，因为简单样本的score $p_t$ 一般接近于1，那么其 $(1-p_t)^\gamma$ 值将会较小，便可以抑制简单样本的权重

三、Focal Loss的实现

以YOLO V4为例，YOLO V4的损失函数由3部分组成：loc(回归损失)、conf(目标置信度损失)、cls(种类损失)，其中需要进行正负样本区分的为目标置信度损失。可以按照以下思路进行处理。

①提取概率p

conf = torch.sigmoid(prediction[..., 4])

②平衡正负样本，设置参数α

torch.where(obj_mask, torch.ones_like(conf) * self.alpha, torch.ones_like(conf) * (1 - self.alpha))

③平衡难易样本，设置参数γ

torch.where(obj_mask, torch.ones_like(conf) - conf, conf) ** self.gamma

④乘回交叉熵损失

ratio       = torch.where(obj_mask, torch.ones_like(conf) * self.alpha, torch.ones_like(conf) * (1 - self.alpha)) * torch.where(obj_mask, torch.ones_like(conf) - conf, conf) ** self.gamma
loss_conf   = torch.mean((self.BCELoss(conf, obj_mask.type_as(conf)) * ratio)[noobj_mask.bool() | obj_mask])

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/181066.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！