一、概述
floyd算法主要作用有:1.找最短路 2.求传递闭包 3.找最小环 4.求出恰好经过k条边的最短路
本文章将介绍floyd求最短路的证明以及以上四个作用的实践。
二、floyd算法求最短路的证明
之前就多次提到过图论与dp问题的联系,floyd算法可以由dp思想来推导
状态表示:d[i,j,k],表示从i点到j点,中间(不包含两头)经过的节点编号不超过k的路径中最短的路径长度。
状态集合:从i点到j点,中间经过节点编号不超过k的所有路径
属性:最短长度
状态计算集合划分:所有不含k号点的路径,所有包含k号点的路径。划分依据是路径选不选k号点
状态转移方程:如果不选k号点,则结果仍为d(k-1,i,j)。如果选择k号点,即在路径中加入k号点。那么怎么样加是能求出最短的那一条呢,答案为从i到k的最短路加上从k到j的最短路。所以状态转移方程为:
根据我们在优化背包问题时积累的知识,我们知道实际上这个数组在计算第k层的时候只用到了k-1层的信息,即可省略k这个维度。dp顺序为:枚举k,枚举i,枚举j,再状态转移。和我们之前提过的floyd算法求最短路一模一样。
三、例题
1.acw1125牛的旅行

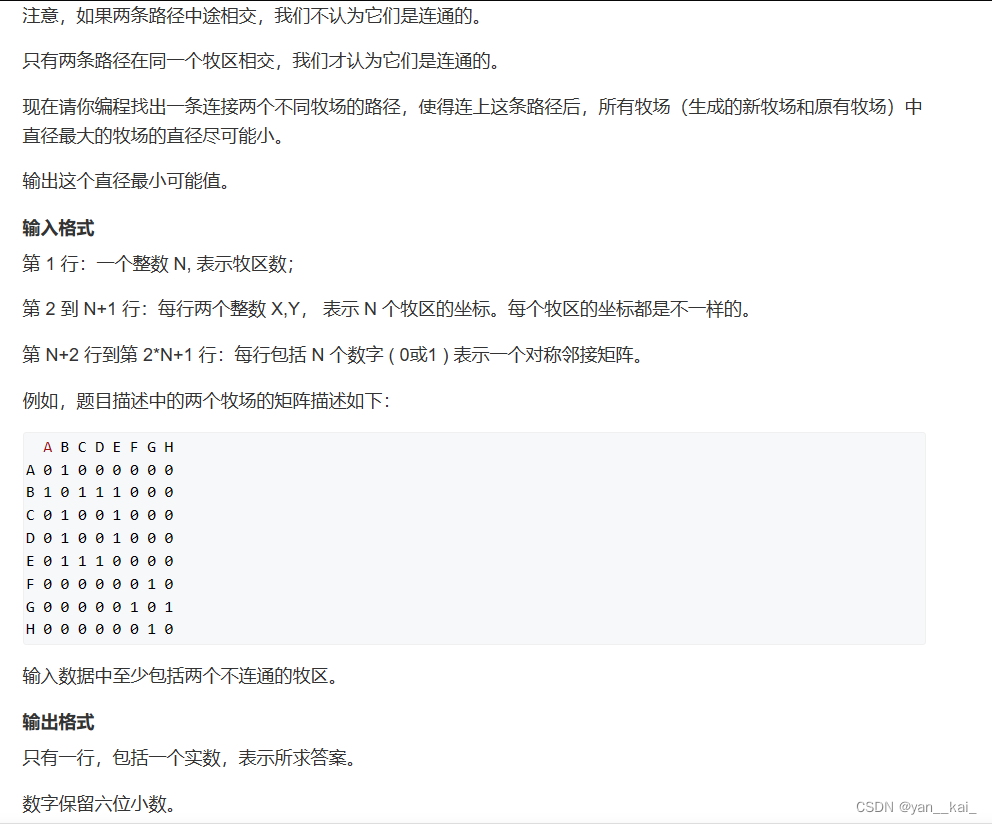
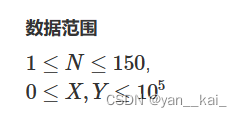
第一眼没我没啥思路,因为n比较小,所以考虑纯纯的暴力做法。
首先思考一下答案组成:如果不连线,最小直径可能是某个连通块里最大的最短路。
如果连线,就直接暴力枚举所有可能连接点i,j。会新生成一条“可能的答案”,即从i点出发到原连通块的最长最短路+i到j+j到原连通块的最长最短路。
floyd算法求最短路,暴力枚举所有点,求出从i点出发到其连通块内的最长的最短路maxd数组。再求maxd的最大值res1。
然后暴力枚举连接i,j。求出产生的最短的“可能答案”res2。
res1为不连边时的直径,如果res1大于res2,则连边后直径不变,答案为res1
如果res1大于res2,则直径变为res2,答案为res2。
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#define x first
#define y second
using namespace std;
const double INF =1e20;
const int N =150;
typedef pair<int,int> PII;
//n很小,可以直接暴力处理出距离第i个点最远的点的距离。
//直径有两种情况 1.不连边,直接就是某个连通块里的直径
//2.暴力遍历连i,j 连边后直径可能是i,j距离+原连通块内离i最远的距离+原连通块内里j最远的距离。
//最终答案是两种情况中的最大值。
PII q[N];
int n;
double d[N][N],maxd[N];
char g[N][N];
double getdist(PII a,PII b)
{
double dx=a.x-b.x,dy=a.y-b.y;
return sqrt(dx*dx+dy*dy);
}
int main()
{
cin>>n;
for(int i=0;i<n;i++) cin>>q[i].x>>q[i].y;
for(int i=0;i<n;i++) cin>>g[i];
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
if(i!=j)
{
if(g[i][j]=='1') d[i][j]=getdist(q[i],q[j]);
else d[i][j]=INF;
}
for(int k=0;k<n;k++)
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
{
d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
}
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
if(d[i][j]<INF)
maxd[i]=max(maxd[i],d[i][j]);
double res1=0;
for(int i=0;i<n;i++) res1=max(res1,maxd[i]);
double res2=INF;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
if(d[i][j]==INF)
{
res2=min(res2,getdist(q[i],q[j])+maxd[i]+maxd[j]);
}
printf("%lf",max(res1,res2));
}
作者:yankai
链接:https://www.acwing.com/activity/content/code/content/4385046/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。2.求传递闭包 acwing343排序

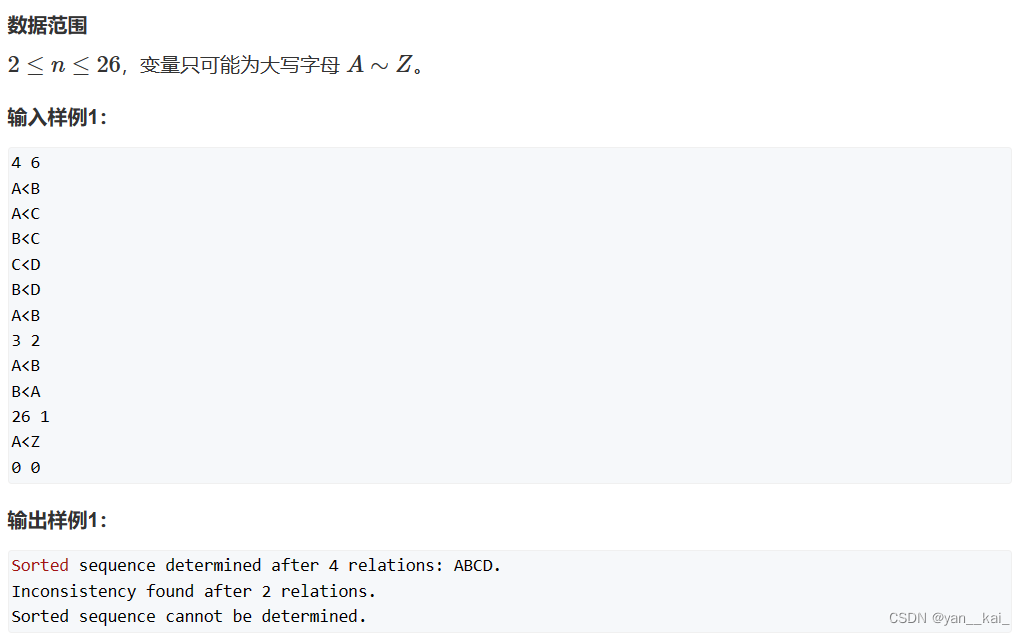
传递闭包 O(mn3)
题意简述:给出若干关系,求出当前信息可求出的所有关系。。其实就是求传递闭包。
根据离散数学知识,对i,j更新n次即为传递闭包,多的不说直接看代码。
如何判断出现矛盾:如果发现:从 x 能到达 y 并且从 y 也能到达 x(即,x 比 y 成绩好并且 y 比 x 成绩好),那就是出现矛盾了。即存在关系(x,x);
题目要求求出从小到大的排序,那我们设置一个求最小值函数,如果i和每个数都有关系,则i是最小值,把i弹出。继续求最小值,求n次即得排序。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N =26;
int n,m;
bool g[N][N],d[N][N];
bool st[N];
void floyd()
{
memcpy(d,g,sizeof g);
for(int k=0;k<n;k++)
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
d[i][j] |=d[i][k]&&d[k][j];
}
int check()
{
for(int i=0;i<n;i++) if(d[i][i]) return 2;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
if(i!=j&&!d[i][j]&&!d[j][i])//存在未确定关系
return 0;
return 1;
}
char getmin()
{
for(int i=0;i<n;i++)
if(!st[i])
{
bool flag=true;
for(int j=0;j<n;j++)
if(!st[j]&&d[j][i]) //j还未输出 且j<i
{
flag=false;
break;
}
if(flag)
{
st[i]=true;
return i+'A';
}
}
}
int main()
{
while(cin>>n>>m,n||m)
{
memset(g,false,sizeof g);
int type=0,t;
for(int i=1;i<=m;i++)
{
char str[5];
cin>>str;
int a=str[0]-'A',b=str[2]-'A';
if(!type)
{
g[a][b]=1;
floyd();//求一遍传递闭包
type=check();//判断是否矛盾或者确定
if(type) t=i;
}
}
if(!type) puts("Sorted sequence cannot be determined.");
else if(type==2) printf("Inconsistency found after %d relations.\n", t);
else
{
memset(st,0,sizeof st);
printf("Sorted sequence determined after %d relations: ", t);
for(int i=0;i<n;i++)
cout<<getmin();
cout<<"."<<endl;
}
}
return 0;
}
作者:yankai
链接:https://www.acwing.com/activity/content/code/content/4385357/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。增量算法 O(mn2)
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 26;
int n, m;
bool d[N][N];
bool st[N];
int check()
{
for (int i = 0; i < n; i ++ )
if (d[i][i])
return 2;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < i; j ++ )
if (!d[i][j] && !d[j][i])
return 0;
return 1;
}
char get_min()
{
for (int i = 0; i < n; i ++ )
if (!st[i])
{
bool flag = true;
for (int j = 0; j < n; j ++ )
if (!st[j] && d[j][i])
{
flag = false;
break;
}
if (flag)
{
st[i] = true;
return 'A' + i;
}
}
}
int main()
{
while (cin >> n >> m, n || m)
{
memset(d, 0, sizeof d);
int type = 0, t;
for (int i = 1; i <= m; i ++ )
{
char str[5];
cin >> str;
int a = str[0] - 'A', b = str[2] - 'A';
if (!type)
{
d[a][b] = 1;
for (int x = 0; x < n; x ++ )
{
if (d[x][a]) d[x][b] = 1;
if (d[b][x]) d[a][x] = 1;
for (int y = 0; y < n; y ++ )
if (d[x][a] && d[b][y])
d[x][y] = 1;
}
type = check();
if (type) t = i;
}
}
if (!type) puts("Sorted sequence cannot be determined.");
else if (type == 2) printf("Inconsistency found after %d relations.\n", t);
else
{
memset(st, 0, sizeof st);
printf("Sorted sequence determined after %d relations: ", t);
for (int i = 0; i < n; i ++ ) printf("%c", get_min());
printf(".\n");
}
}
return 0;
}
作者:yxc
链接:https://www.acwing.com/activity/content/code/content/145995/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。3.acwing344观光之旅(求无向图最小环)

dp思路:和floyd算法类似,按照环上编号最大的点分类。
求每一类的最小值:floyd第k层时,floyd矩阵已知所有点,从i到j只经过1到k-1点的最短路径。
则在此时可求环最小值。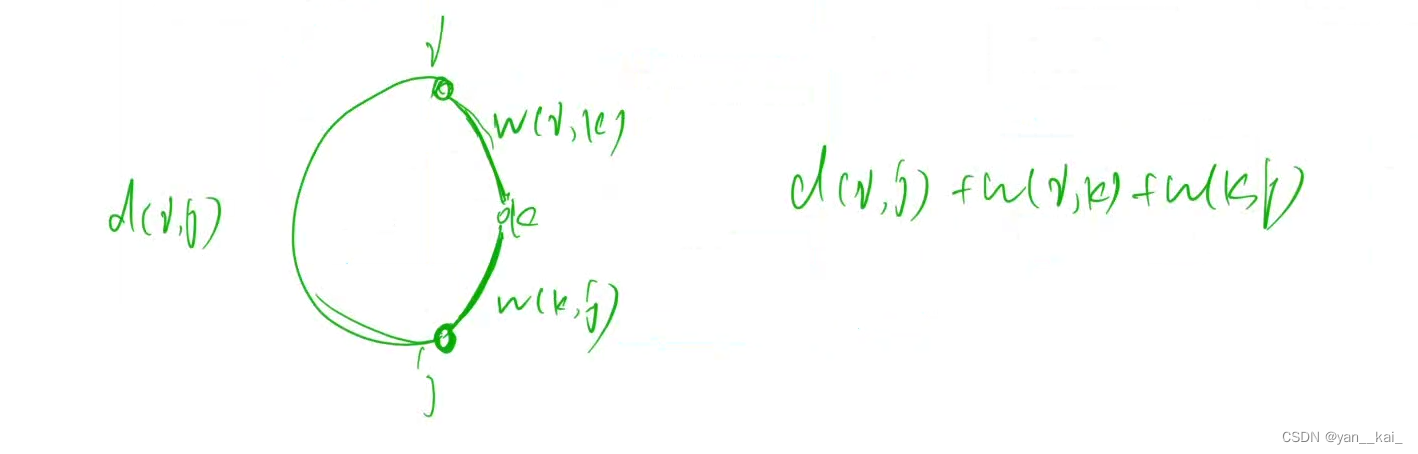
记录方案:floyd算法求更新的点k
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110, INF = 0x3f3f3f3f;
int n, m;
int d[N][N], g[N][N]; // d[i][j] 是不经过点
int pos[N][N]; // pos存的是中间点k
int path[N], cnt; // path 当前最小环的方案, cnt环里面的点的数量
// 递归处理环上节点
void get_path(int i, int j) {
if (pos[i][j] == 0) return; // i到j的最短路没有经过其他节点
int k = pos[i][j]; // 否则,i ~ k ~ j的话,递归处理 i ~ k的部分和k ~ j的部分
get_path(i, k);
path[cnt ++] = k; // k点放进去
get_path(k, j);
}
int main() {
cin >> n >> m;
memset(g, 0x3f, sizeof g);
for (int i = 1; i <= n; i ++) g[i][i] = 0;
while (m --) {
int a, b, c;
cin >> a >> b >> c;
g[a][b] = g[b][a] = min(g[a][b], c);
}
int res = INF;
memcpy(d, g, sizeof g);
// dp思路, 假设k是环上的最大点, i ~ k ~ j(Floyd的思想)
for (int k = 1; k <= n; k ++) {
// 求最小环,
//至少包含三个点的环所经过的点的最大编号是k
for (int i = 1; i < k; i ++) // 至少包含三个点,i,j,k不重合
for (int j = i + 1; j < k; j ++)
// 由于是无向图,
// ij调换其实是跟翻转图一样的道理
// 直接剪枝, j从i + 1开始就好了
// 更新最小环, 记录一下路径
if ((long long)d[i][j] + g[j][k] + g[k][i] < res) {
// 注意,每当迭代到这的时候,
// d[i][j]存的是上一轮迭代Floyd得出的结果
// d[i][j] : i ~ j 中间经过不超过k - 1的最短距离(k是不在路径上的)
res = d[i][j] + g[j][k] + g[k][i];
cnt = 0;
path[cnt ++] = k; // 先把k放进去
path[cnt ++] = i; // 从k走到i(k固定的)
get_path(i ,j); // 递归求i到j的路径
path[cnt ++] = j; // j到k, k固定
}
// Floyd, 更新一下所有ij经过k的最短路径
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= n; j ++)
if (d[i][j] > d[i][k] + d[k][j]) {
d[i][j] = d[i][k] + d[k][j];
pos[i][j] = k;
}
}
if (res == INF) puts("No solution.");
else {
for (int i = 0; i < cnt; i ++) cout << path[i] << ' ';
cout << endl;
}
return 0;
}
作者:Sean今天AC了吗
链接:https://www.acwing.com/solution/content/20140/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。4.floyd算法的边数特性(倍增算法)
设邻接矩阵A,求A的n次幂,易发现a[i][j]为从i到j长度为n条边的路的条数。
类比:设带权矩阵A,求A*A,a[i][j]=min(a[i][k]+a[k][j]) 则为经过了n条边的最短距离。

本题就是类似做法。
首先tmax=100,所以最多用200个点,先离散化以免超时。
然后快速幂算法求倍增。O(n^3*logN)
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
using namespace std;
const int N =210;
int k,n,m,S,E;
int g[N][N];
int res[N][N];
void mul(int c[][N],int a[][N],int b[][N])
{
static int temp[N][N];
memset(temp,0x3f,sizeof temp);
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
temp[i][j]=min(temp[i][j],a[i][k]+b[k][j]);
memcpy(c,temp,sizeof temp);
}
void qmi()
{
memset(res,0x3f,sizeof res);
for(int i=1;i<=n;i++) res[i][i]=0;
while(k)
{
if(k&1) mul(res,res,g);
mul(g,g,g);
k>>=1;
}
}
int main()
{
cin>>k>>m>>S>>E;
memset(g,0x3f,sizeof g);//经过一条边从i到j的最短路 因此i~i是INF
map<int,int> ids;
if(!ids.count(S)) ids[S]=++n;
if(!ids.count(E)) ids[E]=++n;
S=ids[S],E=ids[E];
while(m--)
{
int a,b,c;
cin>>c>>a>>b;
if(!ids.count(a)) ids[a]=++n;
if(!ids.count(b)) ids[b]=++n;
a=ids[a],b=ids[b];
g[a][b]=g[b][a]=min(c,g[a][b]);
}
qmi();
cout<<res[S][E]<<endl;
return 0;
}
作者:yankai
链接:https://www.acwing.com/activity/content/code/content/4395120/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。