假设(X1,X2)为二元高斯随机向量,均值(μ1,μ2),标准差(σ1,σ2),相关系数ρ
定义:X=max(X1,X2),Y=min(X1,X2)
SSTA中计算setup/hold的worst delay时即求X、Y,路径N对应维度为N维。
X的概率密度函数PDF为f(x)=f1(-x)+f2(-x),f1和f2为:
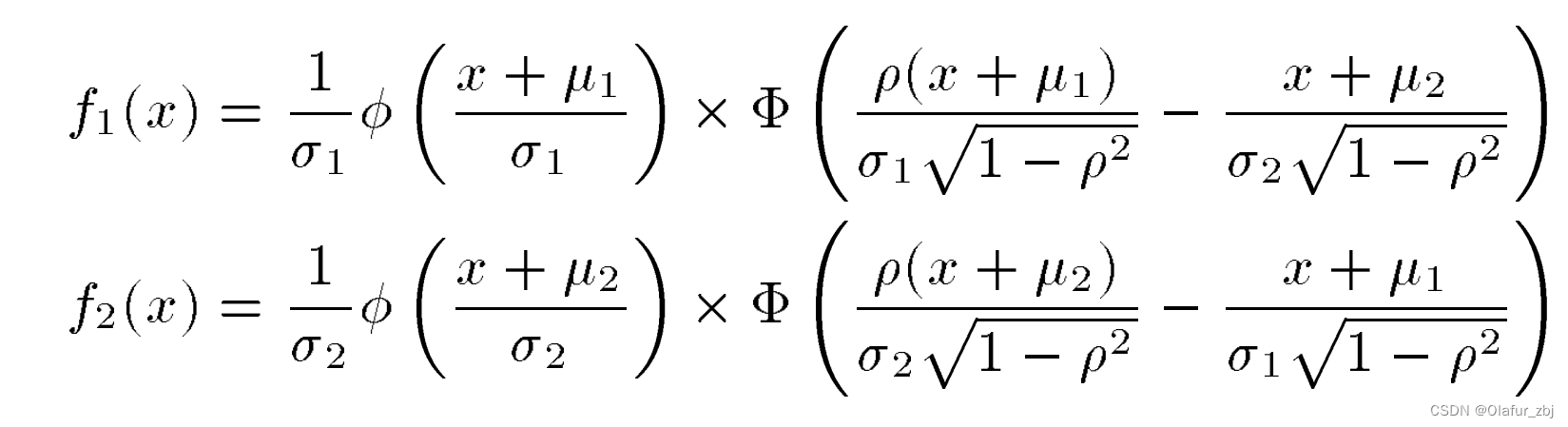
其中小Φ和大Φ分别代表标准正态分布的PDF和CDF(累积分布函数)。
Y的概率密度函数为f(y)=f1(y)+f2(y),f1和f2为:

X和Y的一、二阶矩分别为:
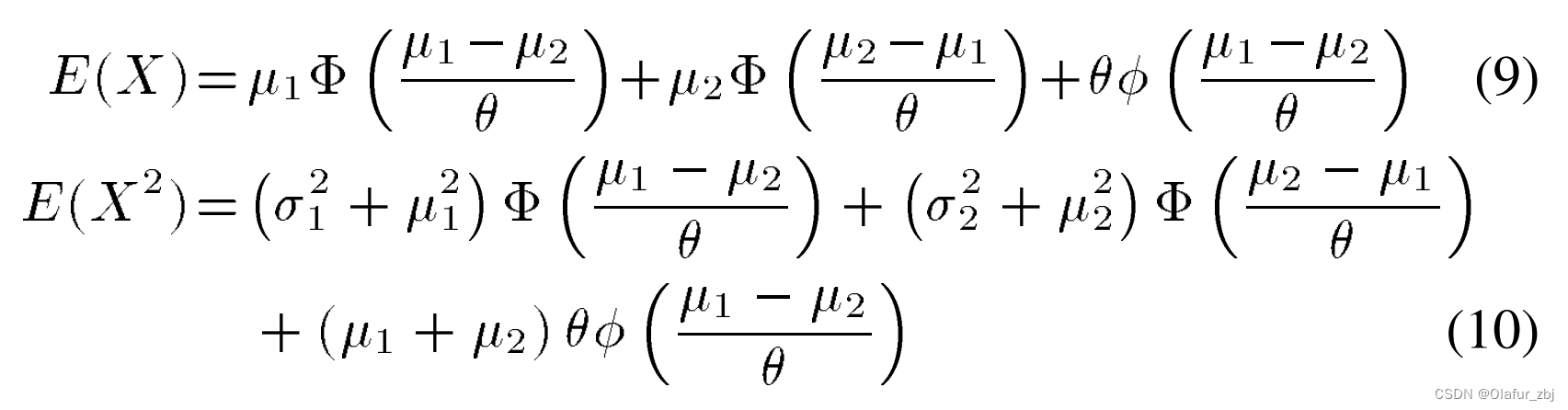
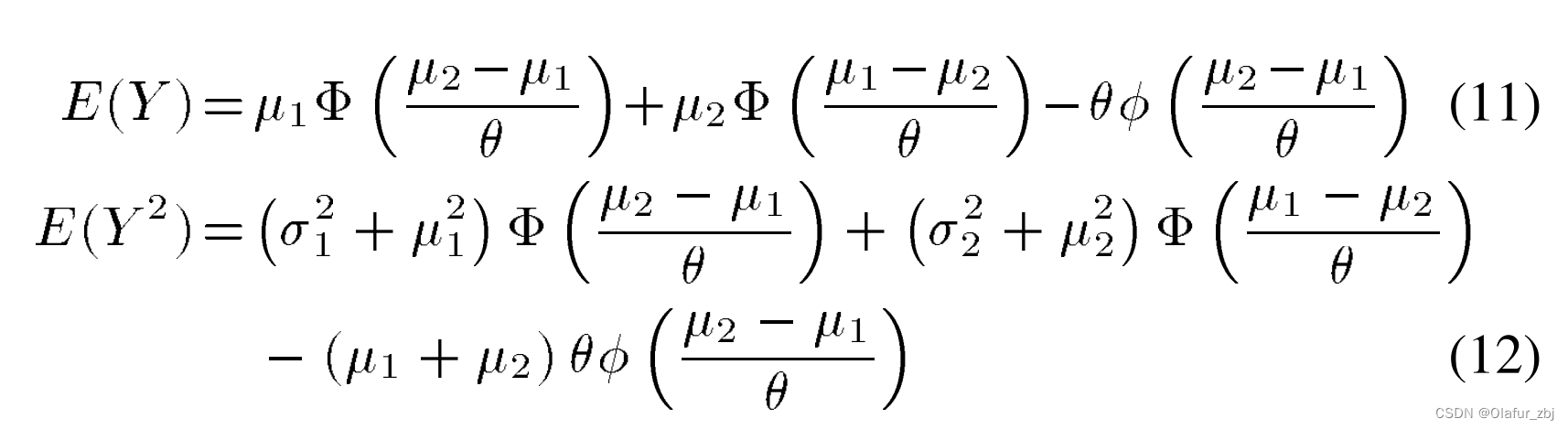
其中θ为:
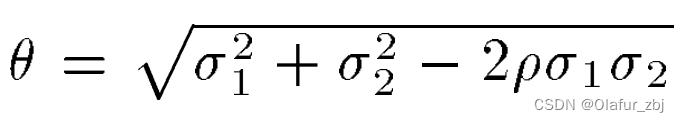
当计算所有路径N的setup/hold worst path时,本质上是计算max(XN)和min(XN),每条路径延时分布为正态分布(SS、TT、FF),当前EDA工具根据路径N中的最大值来计算Fmax(hold与频率无关),但实际上应计算每条路径之间的相关性,根据上述公式计算得到跟真实的统计学意义上的Fmax。
SSTA在计算路径path delay时考虑了每个节点信号合并后(例如与门AND,A1和A2取max(A1,A2))的延时分布,通常假设为一、二阶矩为上式的正态分布,但该假设在两个信号分布方差差异大时会出现严重误差,如图1所示:
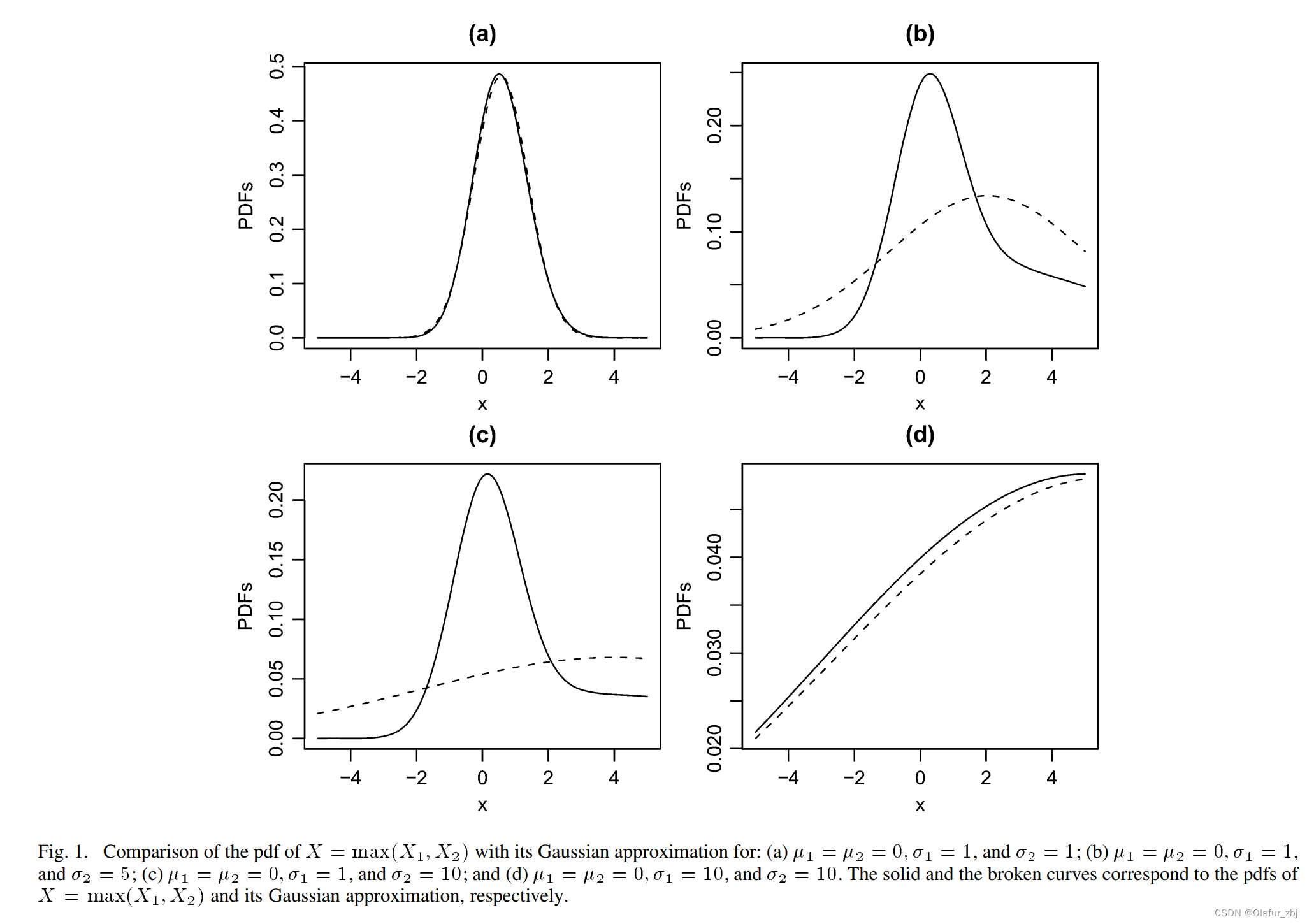
图1中(b)显示,当两条路径标准差为1和5时,假设的误差明显变大,假设更悲观。只有当标准差都很小且非常接近时该假设的误差才较小。
在直接计算N条路径的worst path delay时,如果仅仅使用N条路径中的最差一条作为该STA的最大频率时,会过度乐观。例如fix timing后所有N条path(假设N条都不相关)都修到了400ps(tt corner,ss下是460ps,ff下是340ps,标准差为20ps),当N=1时,芯片最差path delay分布如下,当N=1000时,path delay均值为450ps,标准差为9ps(意味着ss下是477ps,ff下是423ps),N越大,实际芯片的工作频率越低。
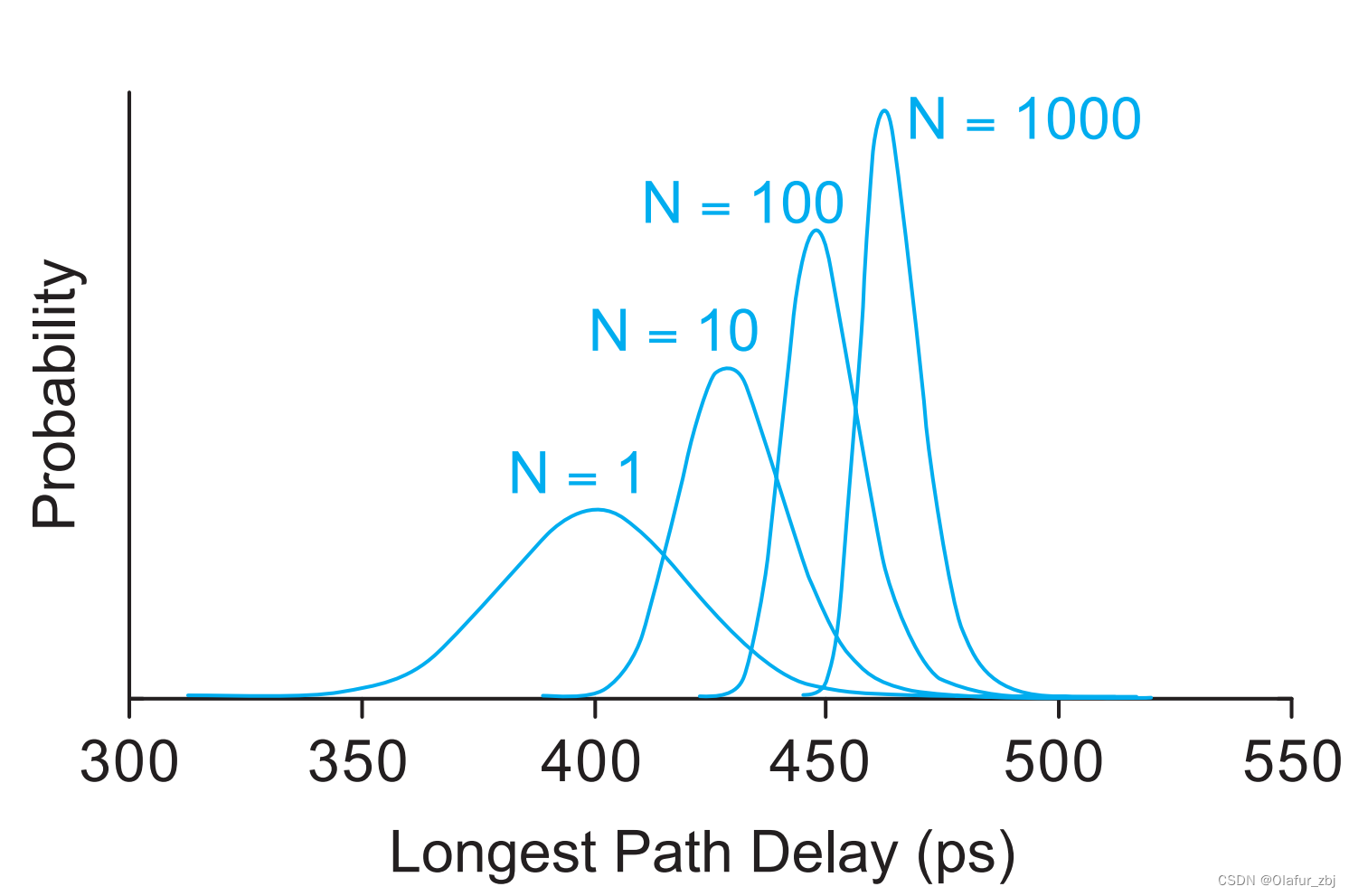
参考资料:
Exact Distribution of the Max/Min of Two Gaussian Random Variables
CMOS VLSI Design A Circuits and Systems Perspective