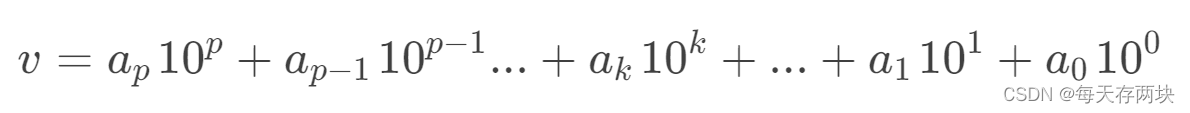本文将以「 通俗易懂」的方式来描述排序的基本实现。

🧑💻阅读本文前,需要一点点编程基础和一点点数据结构知识
本文的所有代码以cpp实现
文章目录
排序的定义
插入排序 ⭐
🧐算法描述
💖具体实现
👽代码实现
☹️性能分析
👻题目练习
希尔排序⭐⭐⭐⭐
🧐算法描述
💖具体实现
👽代码实现
😎性能分析
👻题目练习
冒泡排序⭐
🧐算法描述
💖具体实现
👽代码实现
☹️性能分析
👻题目练习
快速排序⭐⭐⭐⭐
🧐算法描述
💖具体实现
👽代码实现
👻题目练习
😎性能分析
选择排序⭐
🧐算法描述
💖具体实现
👽代码实现
☹️性能分析
👻题目练习
堆排序⭐⭐⭐⭐⭐
🧐算法描述
💖具体实现
👽代码实现
😎性能分析
👻题目练习
归并排序⭐⭐⭐
🧐算法描述
💖具体实现
👽代码实现
😎性能分析
👻题目练习
桶排序⭐⭐⭐
🧐算法描述
💖具体实现
👽代码实现
😎性能分析
👻题目练习
计数排序⭐⭐
🧐算法描述
💖具体实现
👽代码实现
😎性能分析
👻题目练习
基数排序⭐⭐⭐⭐
🧐算法描述
💖具体实现
👽代码实现
😎性能分析
👻题目练习
总结
排序的定义
排序。顾名思义,就是将列表中的元素变为有序的过程。
算法稳定性。若待排序表中有两个元素R1和R2,其对应关键字相同(key1 == key2),且R1在R2前面。排序后R1仍在R2前面,称该算法是稳定的。
接下来简单介绍基本排序算法 ,⭐越多难度越高。

插入排序 ⭐
🧐算法描述
插入排序(Insertion Sort),一般也被称为直接插入排序,是一种简单直观的排序算法。
对于前面 i - 1 个数,已经有序的情况下,将第 i 个插入到合适位置。 这个过程类似于平时打扑克牌时摸牌的操作:右手摸牌,根据牌面大小,放到左手中正确的位置。
💖具体实现
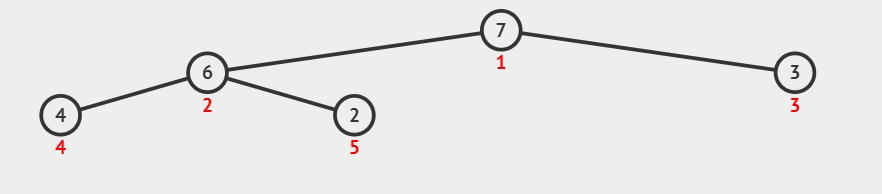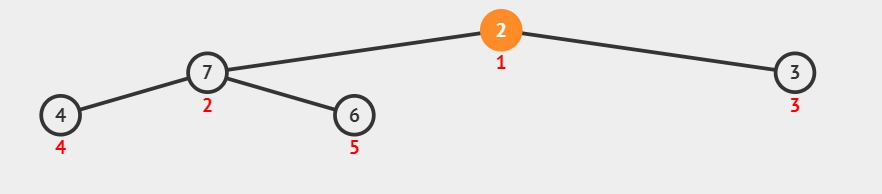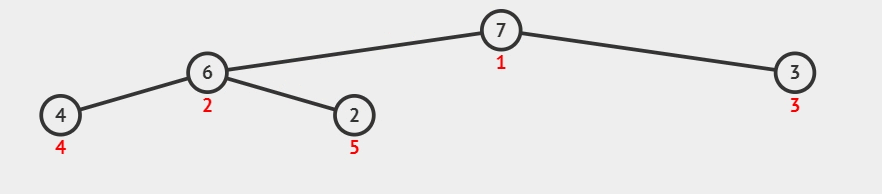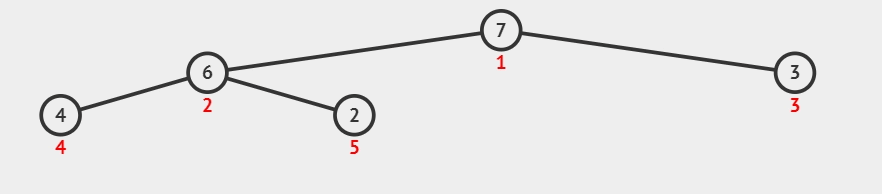
我们以[6, 2, 3, 5, 1, 4]为例 ,演示一下插入排序算法的整个步骤。
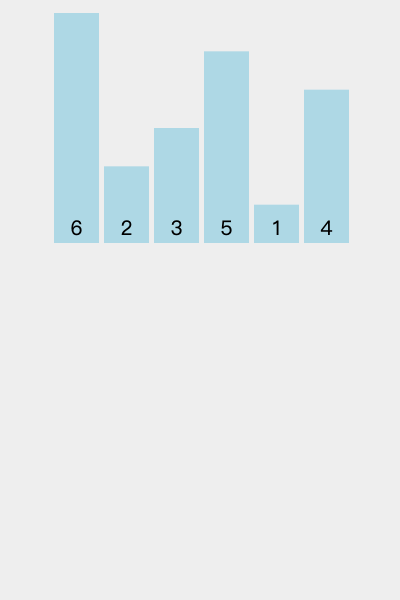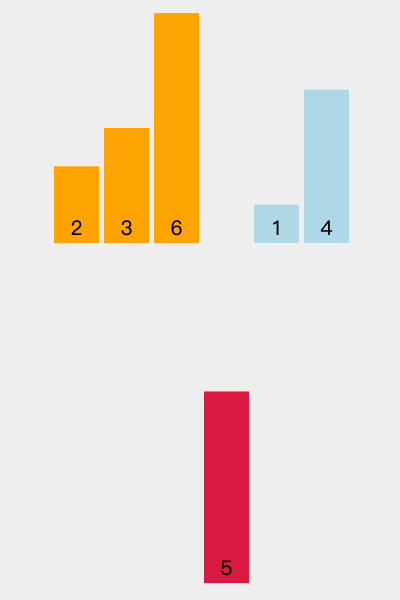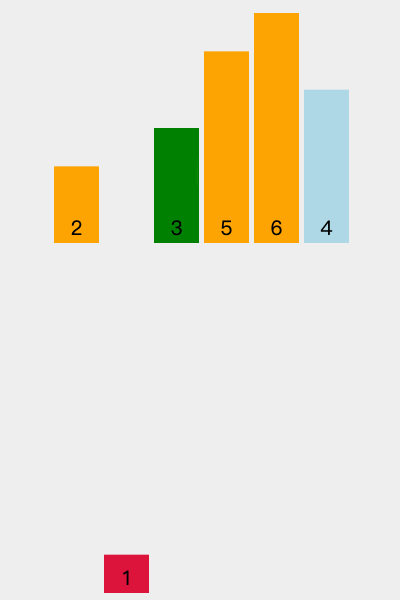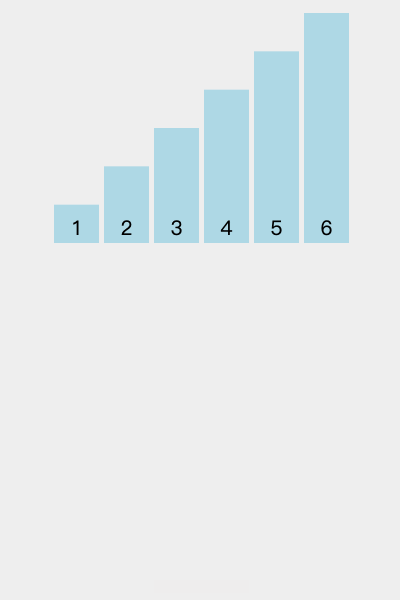
将第一个元素6视为已排序序列,将后面元素依次进行排序。
1)当前的数:2 当前有序列表:6
2 < 6 : 2 放在 6 之前
2)当前的数:3 当前有序列表:2 6
3 < 6 :
3 > 2 : 3 放在 2 之后
3)当前的数:5 当前有序列表:2 3 6
5 > 3 :
5 < 6 : 2 放在 6 之前
4)当前的数:1 当前有序列表:2 3 5 6
1 < 6,1 < 5,1 < 3,1 < 2 :1 放在 2 之前
5)当前的数:4 当前有序列表:1 2 3 5 6
4 < 6,4 < 5
4 > 3:4 放在 3 之后
至此,排序结束。总共进行 n - 1 次循环。排序结果为 1 2 3 4 5 6
👽代码实现
#include <iostream>
using namespace std;
void InsertSort(int a[],int n){
int i,j,tmp; //定义循环变量,和临时变量
for(i = 1; i < n; ++i){ //使用双层循环,外层循环枚举除了第一个元素之外的所有元素
tmp = a[i]; //对于枚举到的元素储存到tmp中
for(j = i - 1; j >= 0; --j){ //内层循环遍历当前元素前面的有序表,进行待插入位置查找
if(tmp <= a[j])
a[j + 1] = a[j]; //若待插入元素<=当前元素a[j],则将a[j]向后移动
else
break;
}
a[j + 1] = tmp; //最后将tmp插入到合适位置
}
}
void Print(int nums[],int n){ //打印列表元素
for(int i = 0; i < n; ++i){
printf("%d ",nums[i]);
}
puts(" ");
}
int main(){
int nums[] = {6,2,3,5,1,4}; //自定义列表
int n = sizeof(nums) / sizeof(nums[0]); //获取列表长度
Print(nums,n);
InsertSort(nums,n); //进行插入排序
Print(nums,n);
return 0;
} ☹️性能分析
时间效率:O(n²)
空间效率:原地排序,O(1)
稳定性:因为每次插入元素时总是从后往前比较再移动,所以不会出现相同位置发生变化的情况,即直接插入排序是一个稳定的算法。
适用性: 顺序存储,链式存储。

这里可以将直接插入排序优化成折半插入排序。简而言之,就是在查找合适位置时进行二分查找,这样可以优化一些时间复杂度,但它只适用于顺序存储。以下是折半插入排序的实现。
void BinnaryInsertSort(int a[],int n){
int i,j,low,high,tmp;
for(int i = 1; i < n; ++i){
tmp = a[i];
low = 0;high = i; //定义二分查找的区间
while(low < high){ //二分查找大于等于tmp中最小的元素
int mid = (low + high) >> 1;
if(a[mid] >= tmp) high = mid;
else low = mid + 1;
}
for(j = i - 1; j >= low; --j) //找到合适位置low,统一后移元素,空出插入位置
a[j + 1] = a[j];
a[j + 1] = tmp;
}
}👻题目练习
【题目描述】 88. 合并两个有序数组 - 力扣(LeetCode)

【解题思路】
将nums2数组视为待排序数组,nums1视为已排序数组。遍历nums2数组将每个元素依次插入到nums1中,copy插入排序的代码,改一下参数即可。
【AC代码】
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int i,j,tmp;
for(i = 0; i < n; ++i){
tmp = nums2[i];
for(j = m + i - 1; j >= 0; --j){
if(tmp <= nums1[j])
nums1[j + 1] = nums1[j];
else
break;
}
nums1[j + 1] = tmp;
}
}
};【题目描述】147. 对链表进行插入排序 - 力扣(LeetCode)
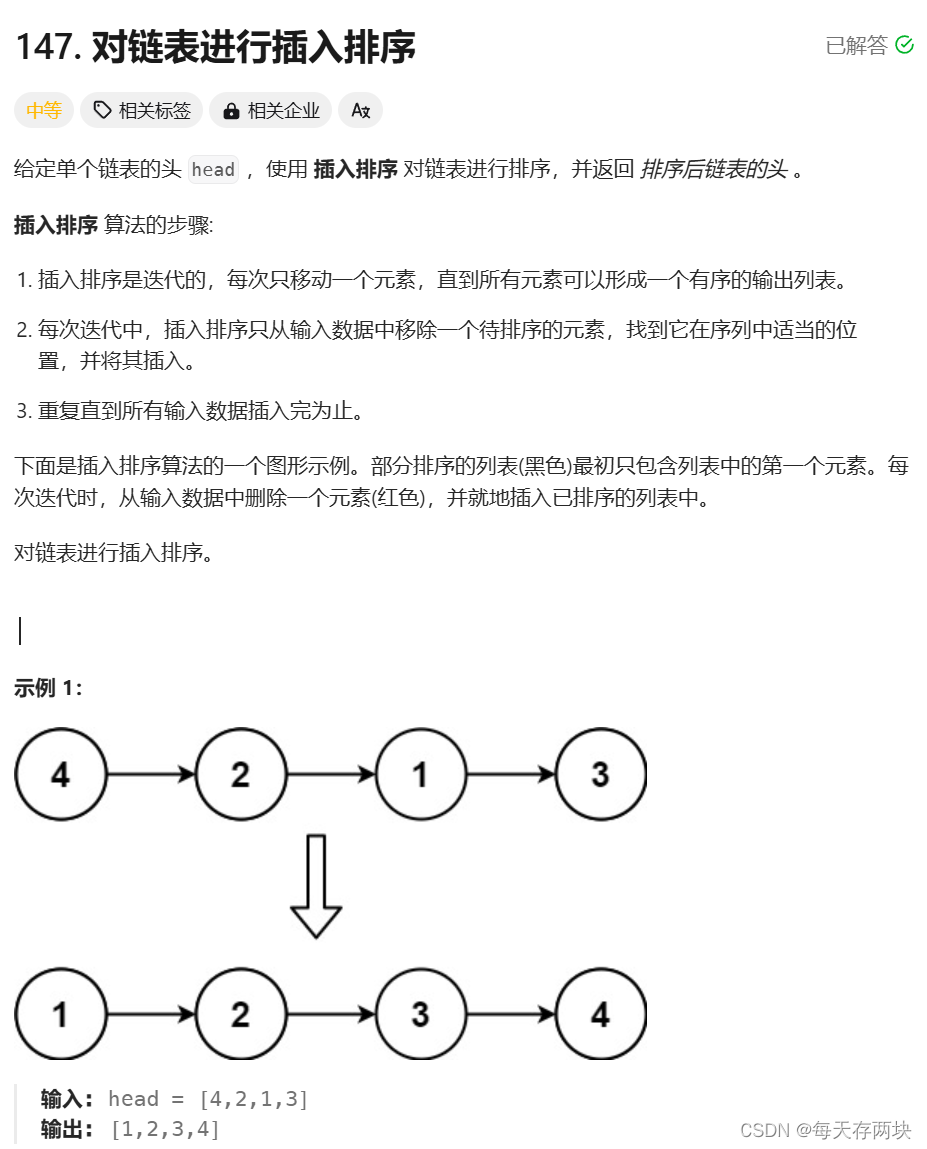
【解题思路】
新建一个链表,遍历原来的链表,对每个结点在有序链表中找合适位置,然后进行插入操作。做链表题必画图,不理解的小伙伴建议画个图。
【AC代码】
class Solution {
public:
ListNode* insertionSortList(ListNode* head) {
if (!head || !head->next) { //空链表返回
return head;
}
ListNode* dummy = new ListNode(-1); //开辟一个虚拟头结点
dummy->next = new ListNode(head->val); //将第一个元素视为已排序元素
ListNode* curr = head->next; //遍历待排序元素
while (curr != nullptr) {
ListNode *prev = dummy, *tmp = curr->next; //双指针方便插入
while (prev->next != nullptr && prev->next->val < curr->val) { //prev->next等同于j,查找合适位置进行插入
prev = prev->next;
}
curr->next = prev->next; //将当前元素插入到合适位置
prev->next = curr;
curr = tmp; //循环遍历下一个结点
}
return dummy->next;
}
};
希尔排序⭐⭐⭐⭐
🧐算法描述
希尔排序(Shell's Sort),也被称为递减增量排序算法(Diminishing Increment Sort),是插入排序的一种更高效的改进排序算法。
先选定一个间隔,把待排序元素分成多个组,所有间隔距离的分在同一组,并在组内进行插入排序。然后减小间隔,重复上述分组和排序的工作。当到达间隔为1时,所有元素在统一组内排好序。
💖具体实现
我们以[9,1,2,5,7,4,8,6,3,5 ]为例,演示一下希尔排序算法的整个步骤。

1)选择一个增量序列gap = n / 2 。图中红色线画中的为第一组。定义一个 i 变量指向这一组的第二个数据,定义一个 j 变量指向 i - gap 的位置。
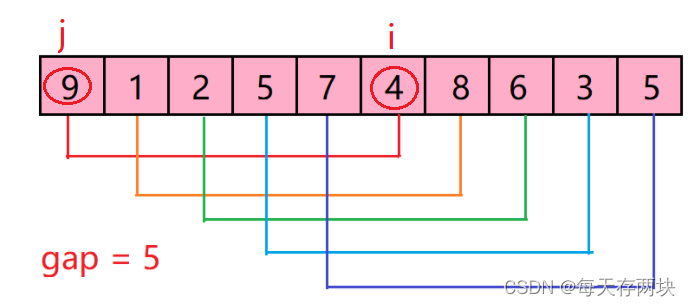
对组内进行插入排序,这里不再赘述,具体实现在上文。排序结果如下:
2) gap 为 2,数据此时分为了两组。
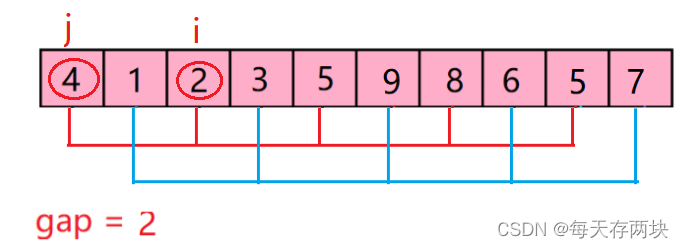
排序结果如下:
 3)gap = 1.
3)gap = 1.
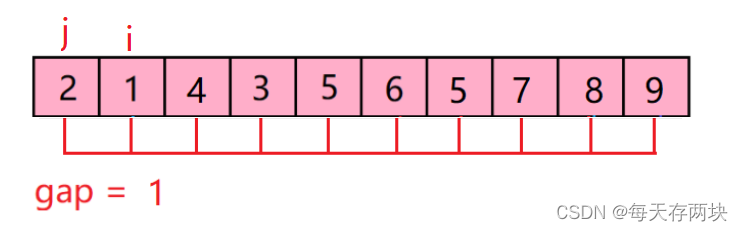
排序结果如下:

👽代码实现
#include <iostream>
using namespace std;
void ShellSort(int a[],int n){
int gap,i,j,tmp;
for(gap = n/2; gap > 0; gap /= 2){ //增量变化(无统一规定)
for(i = gap; i < n; ++i){ //每组内进行插入排序
tmp = a[i];
for(j = i - gap; j >= 0; j -= gap){ //查找合适位置
if(tmp <= a[j]){
a[j + gap] = a[j]; //将元素后移
}else
break;
}
a[j + gap] = tmp; //插入合适位置
}
}
}
void Print(int nums[],int n){ //打印数组
for(int i = 0;i < n; ++i){
printf("%d ",nums[i]);
}
puts(" ");
}
int main(){
int nums[] = {9,1,2,5,7,4,8,6,3,5}; //自定义数组
int n = sizeof(nums)/sizeof(nums[0]); //获取数组长度
Print(nums,n);
ShellSort(nums,n); //进行希尔排序
Print(nums,n);
return 0;
} 😎性能分析
时间效率:一般O(n^1.3),最坏O(n²)
空间效率:原地排序,O(1)
稳定性:当相同关键字的记录被划分到不同的子表时,可能会改变他们之间的相对次序,因此希尔排序是一个不稳定的算法。
适用性: 仅适用于顺序存储的线性表。
👻题目练习
【题目描述】506. 相对名次 - 力扣(LeetCode)

【解题思路】
对数组进行希尔排序成一个排名数组。遍历原数组,在排名数组中二分查找元素的下标。然后按照要求完成即可
这里用二分查找可以将复杂度将到O(long₂ⁿ),乘上外层循环O(n),加上希尔排序复杂度O(nlong₂ⁿ),总的时间复杂度为O(long₂ⁿ)。
【AC代码】
class Solution {
public:
vector<string> findRelativeRanks(vector<int>& score) {
vector<int> Rank = ShellSort(score); //对数组进行希尔排序
vector<string> ans;
for(int x : score){
int i = binnaryFind(x,Rank); //二分查找下标
if(i + 1 == 1) ans.push_back("Gold Medal");
else if(i + 1 == 2) ans.push_back("Silver Medal");
else if(i + 1 == 3) ans.push_back("Bronze Medal");
else ans.push_back(to_string(i + 1));
}
return ans;
}
vector<int> ShellSort(vector<int> a){
int n = a.size();
int gap,i,j,tmp;
for(gap = n/2; gap > 0; gap /= 2){
for(i = gap; i < n; ++i){ //每组内进行插入排序
tmp = a[i];
for(j = i - gap; j >= 0; j -= gap){ //查找合适位置
if(tmp >= a[j]){
a[j + gap] = a[j]; //将元素后移
}else
break;
}
a[j + gap] = tmp; //插入合适位置
}
}
return a;
}
int binnaryFind(int x,vector<int> Rank){
int left = 0,right = Rank.size() - 1;
while(left < right){
int mid = (left + right) >> 1;
if(Rank[mid] > x) left = mid + 1;
else right = mid;
}
return left;
}
};冒泡排序⭐
🧐算法描述
冒泡排序(Bubble Sort)又称为泡式排序,是一种简单的排序算法。
通过比较相邻元素,使较大的元素不断往后冒,从而实现排序的过程。
这个算法名字的由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端(升序或降序排列),就像水中的气泡会冒起来一样。
💖具体实现
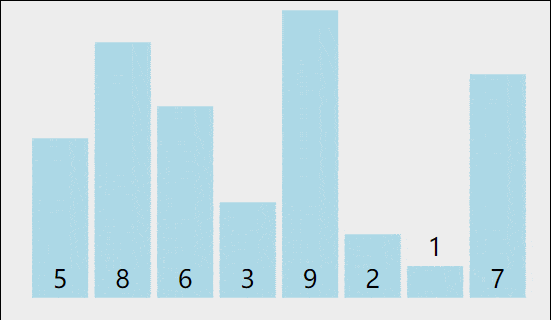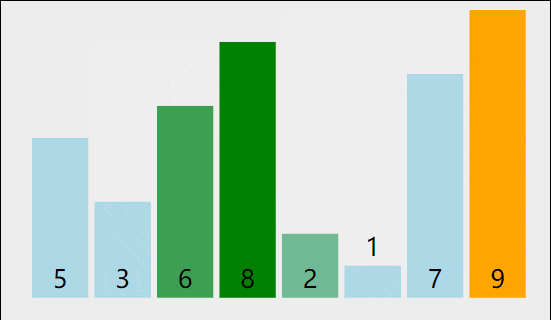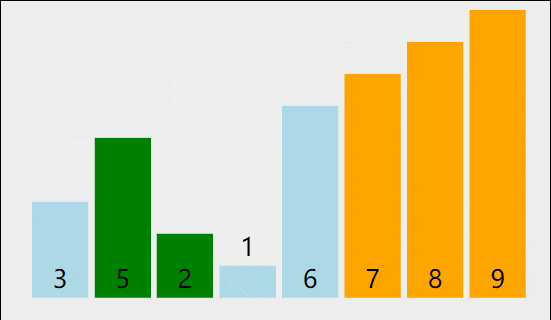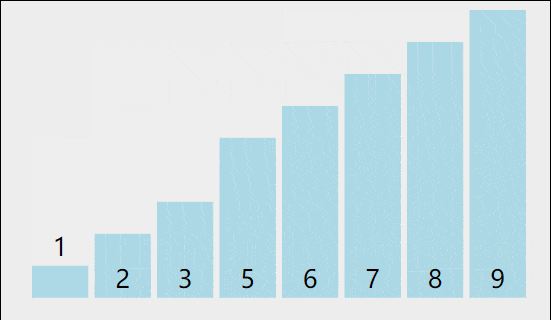
我们以[5,8,6,3,9,2,1,7]为例,演示一下冒泡排序算法的整个步骤。
1)比较相邻的元素。如果第一个比第二个大,就交换它们两个。
2)对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
3)针对所有的元素重复以上的步骤,除了最后一个。
4)持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
👽代码实现
#include <iostream>
using namespace std;
void BubbleSort(int a[],int n){
for(int i = n - 1; i >= 0; --i){ //外层循环进行 n - 1 趟排序
bool flag = false; //表示本趟冒泡是否发生交换
for(int j = 0; j < i; ++j){ //每一趟冒泡过程
if(a[j + 1] < a[j]) swap(a[j + 1],a[j]);
flag = true;
}
if(flag == false) return ; //本趟遍历没有发生交换,说明表已经有序
}
}
void Print(int nums[],int n){ //打印数组
for(int i = 0;i < n; ++i){
cout<<nums[i]<<' ';
}
puts(" ");
}
int main(){
int nums[] = {5,8,6,3,9,2,1,7}; //自定义数组
int n = sizeof(nums)/sizeof(nums[0]); //获取数组大小
Print(nums,n);
BubbleSort(nums,n); //进行冒泡排序
Print(nums,n);
return 0;
} ☹️性能分析
时间效率:O(n²)。加入flag后,当初始序列有序时,显然第一冒泡后flag为false(本趟没有元素交换),从而直接跳出循环,比较n-1次,移动次数为0,从而最好的时间复杂度为O(n)。
空间效率:原地排序,O(1)
稳定性:稳定
适用性: 顺序存储,链式存储的线性表。
👻题目练习
【题目描述】75. 颜色分类 - 力扣(LeetCode)

【解题思路】
直接copy冒泡排序。
【AC代码】
class Solution {
public:
void sortColors(vector<int>& nums) {
int n = nums.size();
for(int i = n - 1; i >= 0; --i){
bool flag = false;
for(int j = 0; j < i; ++j){
if(nums[j + 1] < nums[j]) swap(nums[j + 1],nums[j]);
flag = true;
}
if(flag == false) return ;
}
}
};快速排序⭐⭐⭐⭐
🧐算法描述
快速排序 (Quick Sort)是利用了「 分而治之 」的思想,进行递归计算的排序算法,效率在众多排序算法中的佼佼者。
快速排序是冒泡排序的改进版。随机找到一个位置,将比它小的数都放到它 左边 ,比它大的数都放到它 右边,然后分别 递归 求解 左边 和 右边 使得两边分别有序。
C++ 标准库的
std::sort()函数通常使用快速排序作为默认实现。
💖具体实现
快速排序实现有多种,以下是我常用方式实现。
我们以 [4, 1, 6, 2 ,9, 3]为例,演示一下快速排序算法的整个步骤。
1)第一遍遍历
- 在 [4,1,6,2,9,3] 中选择元素 4 作为基准数
- 检查是否 1 < 4 (基准数)
- 检查是否 6 < 4 (基准数)
- 检查是否 2 < 4 (基准数)
- 2 < 4 (基准数) 是为真,将指数2和 存储指数 6 进行交换
- 检查是否 9 < 4 (基准数)
- 检查是否 3 < 4 (基准数)
- 3 < 4 (基准数) 为真,将指数3和存储指数6 进行交换
- 最后,将基准数 4 和 最右边绿色的数 3 (小于等于基准数的最大数)进行交换
- 此时基准数4左边全部小于4,右边大于4
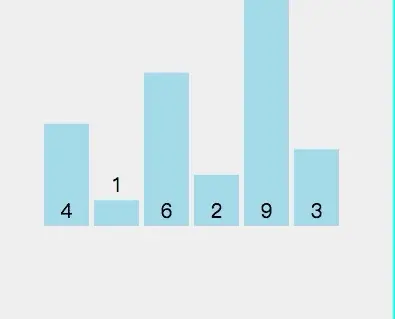
此时数组顺序为[3,1,2,4,9,6]。
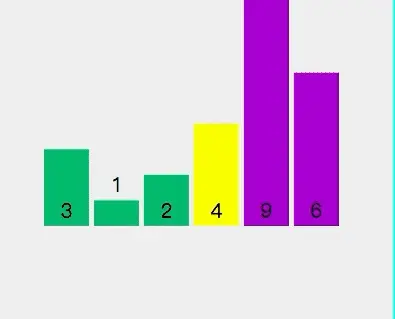
2)下一步
- 递归进行左边排序
- 选择元素 3 作为基准数
- 检查是否 1 < 3 (基准数)
- 检查是否 2 < 3 (基准数)
- 将基准数 3和存储指数值 2进行交换
- 现在基准数已经在排序过后的位置
- 进行拆分 [2,1] 选择 2 作为轴心点
- 检查是否 1 < 2 (基准数)
- 左边遍历完成,将基准数2和存储指数1 进行交换
3)递归进行右边排序,这里不再赘述。
👽代码实现
#include <iostream>
using namespace std;
int Partition(int a[],int start,int end){ //在start与end区间寻找基准数的下标
int pivot = start; //定义第一个元素为基准数
int j = start + 1; //j为大于基准数的数的左边界
for(int i = start + 1; i < end + 1; ++i){ //遍历区间元素
if(a[i] <= a[pivot]){
swap(a[i],a[j]); //保证j以前的数都是小于等于基准数
++j;
}
}
swap(a[j - 1],a[pivot]); //将基准数与小于等于基准数的最大数进行交换,也就是那个最右边绿色的数
pivot = j - 1; //更新基准数下标
return pivot;
}
void QuickSort(int a[],int start,int end){
if(start >= end) return ;
int pivot = Partition(a,start,end); //获取基准数
QuickSort(a,start,pivot - 1); //递归排序左区间
QuickSort(a,pivot + 1,end); //递归排序右区间
}
void Print(int nums[],int n){ //打印数组
for(int i = 0; i < n; ++i){
cout<<nums[i]<<' ';
}
puts(" ");
}
int main(){
int nums[] = {4,1,6,2,9,3};
int n = sizeof(nums)/sizeof(nums[0]); //获取数组长度
Print(nums,n);
QuickSort(nums,0,n - 1); //进行快速排序
Print(nums,n);
return 0;
} 👻题目练习
【题目描述】 217. 存在重复元素 - 力扣(LeetCode)

【解题思路】
对数组进行排序,然后对数组元素进行两两比较,若相同说明存在,否则不存在相同元素。
【AC代码】
直接调用c++封装好的sort函数
class Solution {
public:
bool containsDuplicate(vector<int>& nums) {
sort(nums.begin(),nums.end()); //排序数组
for(int i = 1; i < nums.size(); ++i){
if(nums[i] == nums[i - 1])
return true;
}
return false;
}
};😎性能分析
时间效率:一般为O(nlong₂ⁿ)。快排整体的综合性能和使用场景都是比较好的,所以叫快速排序。
空间效率:栈的深度O(n)
稳定性:在划分算法中,若右端关键字,且均小于基准数的记录,则在交换到左端区间后,他们的相对位置会发生变化,即快速排序是一种不稳定的排序算法。
适用性: 仅适用于顺序存储的线性表。
快速排序 在众多排序算法中效率较高,平均时间复杂度为O(nlong₂ⁿ)。但当完全有序时,最坏时间复杂度达 到最坏情况 O(n²)。 所以每次在选择基准数的时候,我们可以尝试用随机的方式选取,这就是 随机快速排序 。

想象一下在随机化版本的快速排序中,随机化数据透视选择,我们不会总是得到 0,1 和 n-1 这种非常差的分割。所以不会出现上文提到的问题。
随机快速排序只需要修改 Partition 函数,使其随机选择基准元素即可。像这样:
int idx = start + rand() % (end - start + 1);// 生成随机下标
swap(a[idx], a[end]); // 将随机选择的元素与末尾元素交换
int pivot = start; 选择排序⭐
🧐算法描述
选择排序(Selection sort)是一种简单直观的排序算法。
第一次从待排序的数据元素种选出最小(或最大)的一个元素,存放在排序序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素 的个数为零。
选择排序中的关键在于,怎么找出一堆数据中最小(或最大)的。
💖具体实现
我们以[6, 2, 3, 5, 1, 4]为例,演示一下选择排序算法的整个步骤。
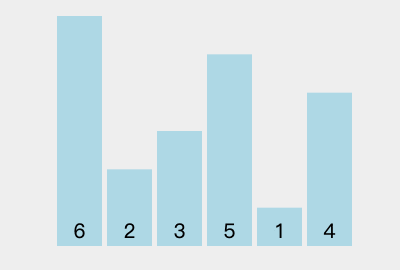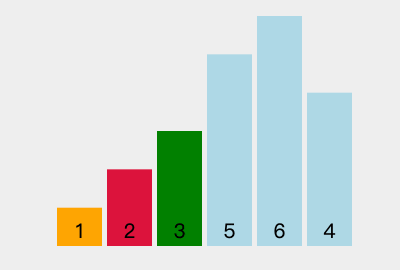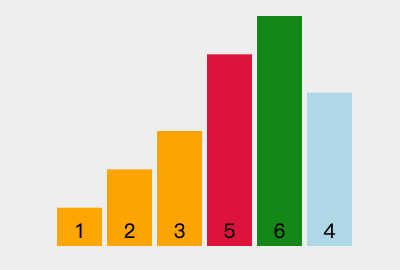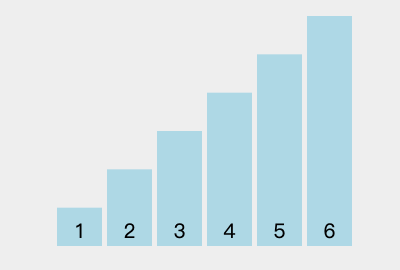
第一次参与比较的数据:6 2 3 5 1 4
1)第一次循环:在 2 3 5 1 4 中找出最小值:1 。与最左边的值进行交换后:1 2 3 5 6 4
2)第二次循环:在 2 3 5 6 4 中找出最小值:2 。与最左边的值进行交换后:1 2 3 5 6 4
3)第三次循环:在 3 5 6 4 中找出最小值:3 。与最左边的值进行交换后:1 2 3 5 6 4
4)第四次循环:在 5 6 4 中找出最小值:4 。与最左边的值进行交换后:1 2 3 4 6 5
5)第五次循环:在 6 5 中找出最小值:5 。与最左边的值进行交换后:1 2 3 4 5 6
👽代码实现
和冒泡排序相比,选择排序比冒泡排序的效率高,高在交换位置的次数上。选择排序的交换位置是有意义的,循环 一次,然后找出参加比较的这堆数据中最小的,拿着这个最小的值和最前面的数据交换位置。
#include <iostream>
using namespace std;
void SelectionSort(int a[],int n){
for(int i = 0;i < n - 1; ++i){ //进行 n - 1 趟
int min = i; //记录最小元素位置
for(int j = i + 1; j < n; ++j){ //在剩余未排序元素中找最小
if(a[j] < a[min]) min = j; //将最小元素下标记录
}
swap(a[i],a[min]); //与第一个元素交换
}
}
void Print(int a[],int n){ //打印数组
for(int i = 0; i < n; ++i){
printf("%d ",a[i]);
}
puts("");
}
int main(){
int a[] = {6,2,3,5,1,4};
int n = sizeof(a)/sizeof(a[0]); //获取数组长度
Print(a,n);
SelectionSort(a,n); //进行选择排序
Print(a,n);
return 0;
}☹️性能分析
时间效率:O(n²)。
空间效率:原地排序,O(1)
稳定性:在第 i 趟找到最小元素后,和第 i 个元素交换,可能会导致第 i 个元素与含有相同关键字的元素的相对位置发生改变。选择排序是一种不稳定的算法
适用性: 顺序存储,链式存储的线性表。
👻题目练习
【题目描述】611. 有效三角形的个数 - 力扣(LeetCode)

【解题思路】
组成三角形的条件是:任意两边之和大于第三边。
将数组排序,然后多维枚举,将最大的一条边固定,再枚举另外两条边并判断是否满足条件,满足条件计数器加1。
当然这个算法的时间复杂度达到O(n³),有兴趣的小伙伴可以进行二分查找降低复杂度。
【AC代码】
以下是c语言代码,怕c++会超时
void SelectionSort(int a[],int n){
for(int i = 0;i < n - 1; ++i){
int min = i;
for(int j = i + 1; j < n; ++j){
if(a[j] < a[min]) min = j;
}
int temp = a[i];
a[i] = a[min];
a[min] = temp;
}
}
int triangleNumber(int* nums, int numsSize) {
SelectionSort(nums,numsSize); //对数组进行选择排序
int ans = 0;
for(int k = numsSize - 1; k >= 0; --k){
int c = nums[k];
for(int i = k - 1; i >= 0; --i){
int a = nums[i];
for(int j = i - 1; j >= 0; --j){
int b = nums[j];
if(a + b > c) ++ans; //满足条件计数器加一
else break;
}
}
}
return ans;
}堆排序⭐⭐⭐⭐⭐
🧐算法描述
堆排序(Heap Sort) 就是利用了堆的性质进行排序。
堆是一棵完全二叉树(除了最底层,其他层的节点都是满的,最底层的节点都尽量靠左排列。)不理解完全二叉树的小伙伴可以去看我的数据结构树那块的内容:数据结构--树
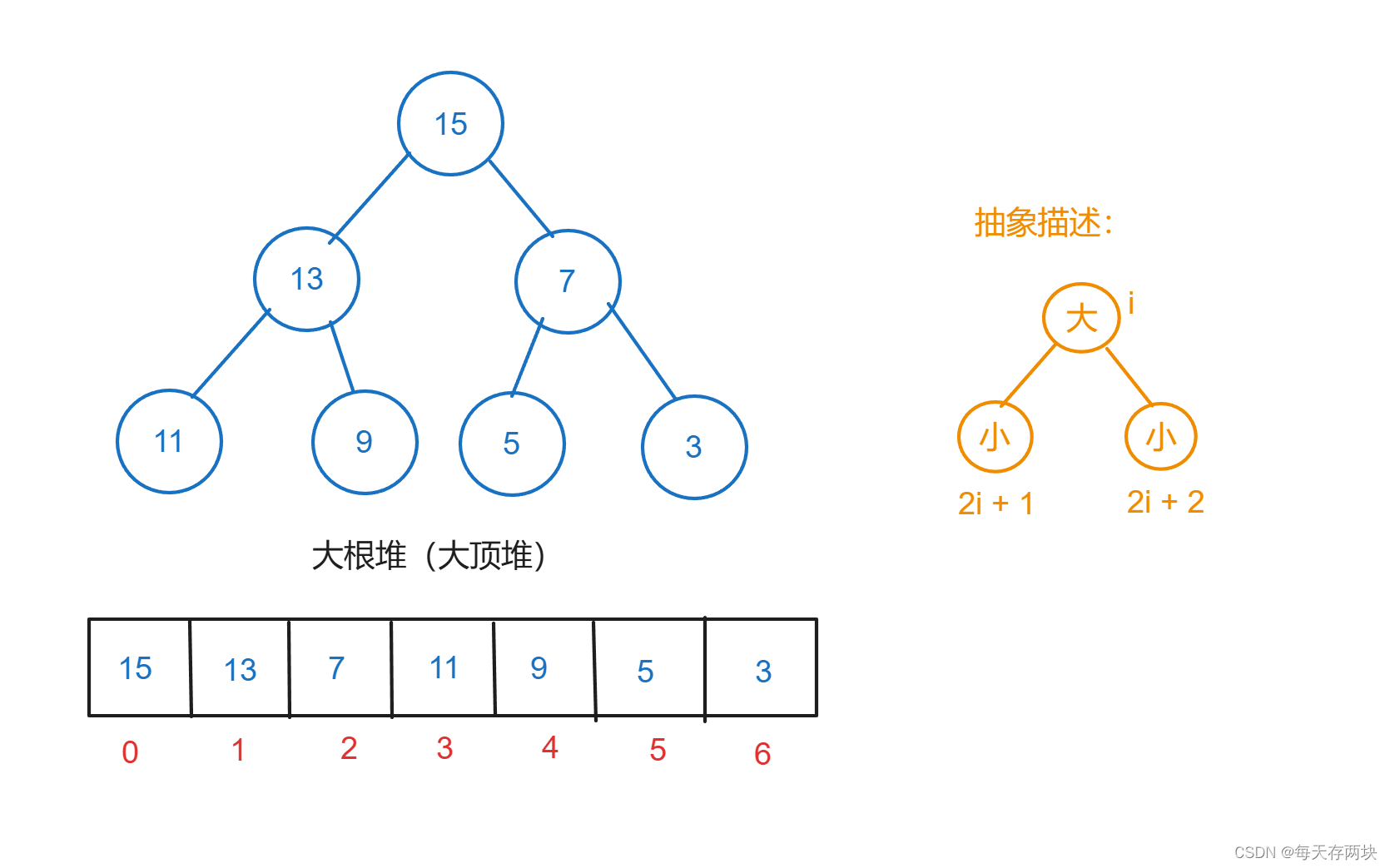
为方便理解算法,这里简单介绍一下什么是堆:
堆是一种特殊的树形数据结构,通常用于实现优先队列。因为堆能够快速找到最大(最小)元素。堆通常是一个可以被看做是一棵树的数组对象。
堆的性质:在一个小根堆(Min Heap)中,对于每个父节点 i 的值都小于或等于其子节点的值。在一个大根堆(Max Heap)中,对于每个父节点 i 的值都大于或等于其子节点的值。
堆可以通过数组(下标从0开始)来表示,具体来说,对于数组中的第 i 个元素:
- 其父节点位于位置
floor((i-1)/2) - 其左子节点位于位置
(2*i + 1) - 其右子节点位于位置
(2*i + 2)
像这样:
💖具体实现
我们以[2, 6, 3, 4,7]为例,演示一下堆排序算法的整个步骤。
1)构建初始大顶堆:
- 定义一个数组实现的堆结构,将原始数组的元素依次存入堆结构的数组中(初始顺序不变)。
- 从数组的中间位置开始,从右至左,依次通过「下沉调整」将数组转换为一个大顶堆。
所谓下沉调整:
如果当前节点为叶子节点或者没有子节点,那么不需要进行调整,堆的性质已经满足。
否则,找到当前节点的较大(大顶堆)子节点。交换当前节点与其较大子节点的值。
继续向下检查被交换的子节点,重复步骤 2,直到当前节点满足堆序性质或成为叶子节点。
2)交换元素,调整堆:
- 交换堆顶元素(第 1个元素)与末尾(最后 1个元素)的位置,交换完成后,堆的长度减 1。
- 交换元素之后,由于堆顶元素发生了改变,需要从根节点开始,对当前堆进行「下沉调整」,使其保持堆的特性。
3)重复交换和调整堆:重复第 2 步,直到堆的大小为 1 时,此时大顶堆的数组已经完全有序
👽代码实现
#include <iostream>
using namespace std;
void maxHeapify(int a[],int n,int i){ //维护大根堆
int largest = i; //记录最大数的下标
int lson = i * 2 + 1; //当前结点的左孩子
int rson = i * 2 + 2; //当前结点的右孩子
//找三个节点中最大的
if(lson < n && a[largest] < a[lson])
largest = lson;
if(rson < n && a[largest] < a[rson])
largest = rson;
if(largest != i){
swap(a[largest],a[i]); //交换最大元素
maxHeapify(a,n,largest); //递归交换最大元素
}
}
void HeapSort(int a[],int n){
//初始化堆 父节点下标 = (i - 1)/2
for(int i = n / 2 - 1; i >= 0; --i) //数组最后下标从n-1开始
maxHeapify(a,n,i);
//排序
for(int i = n - 1; i > 0; --i){
swap(a[i],a[0]); //交换堆顶元素与堆的最后一个元素
maxHeapify(a,i,0); //继续维护剩余的元素
}
}
void Print(int a[],int n){ //打印数组
for(int i = 0;i < n; ++i){
printf("%d ",a[i]);
}
puts("");
}
int main(){
int a[] = {5,2,7,3,6,1,4};
int n = sizeof(a)/sizeof(a[0]); //获取数组长度
Print(a,n);
HeapSort(a,n); //进行堆排序
Print(a,n);
return 0;
}😎性能分析
时间效率:O(nlong₂ⁿ)。
空间效率:原地排,O(1)
稳定性:在进行「下沉调整」时,相等元素的相对位置可能会发生变化。因此,堆排序是一种 不稳定排序算法。
适用性:仅适用于顺序存储的线性表
👻题目练习
【题目描述】LCR 159. 库存管理 III - 力扣(LeetCode)

【解题思路】
对数组进行排序,返回前cnt个数即可。
【AC代码】
建议自己手写一遍,加深对算法的印象
class Solution {
public:
vector<int> inventoryManagement(vector<int>& stock, int cnt) {
HeapSort(stock);
vector<int> ans;
for(int i = 0; i < cnt; ++i) ans.push_back(stock[i]);
return ans;
}
void HeapSort(vector<int>& a){
int n = a.size();
for(int i = n / 2 - 1; i >= 0; --i)
maxHeapify(a,n,i);
for(int i = n - 1; i > 0; --i){
swap(a[i],a[0]);
maxHeapify(a,i,0);
}
}
void maxHeapify(vector<int>& a,int n,int i){
int largest = i;
int lson = i * 2 + 1;
int rson = i * 2 + 2;
if(lson < n && a[largest] < a[lson])
largest = lson;
if(rson < n && a[largest] < a[rson])
largest = rson;
if(largest != i){
swap(a[largest],a[i]);
maxHeapify(a,n,largest);
}
}
};归并排序⭐⭐⭐
🧐算法描述
归并排序(Merge Sort):采用经典的分治策略,先递归地将当前数组平均分成两半,然后将有序数组两两合并,最终合并成一个有序数组。
通过将当前乱序数组分成长度近似的两份,分别进行「 递归 」调用,然后再对这两个排好序的数组,利用两个游标,将数据元素依次比较,选择相对较小的元素存到一个「 辅助数组 」中,再将「 辅助数组 」中的数据存回「 原数组 」。
💖具体实现
我们以[0,5,7,3,1,6,8,4] 为例,演示一下归并排序算法的整个步骤。

- 分解过程:先递归地将当前数组平均分成两半,直到子数组长度为 1。
- 找到数组中心位置 mid,从中心位置将数组分成左右两个子数组 。
- 对左右两个子数组分别进行递归分解。
- 最终将数组分解为 n 个长度均为 1的有序子数组。
- 归并过程:从长度为 1 的有序子数组开始,依次将有序数组两两合并,直到合并成一个长度为 n 的有序数组。
- 使用临时数组复制原数组。
- 使用两个指针 𝑙_pos、𝑟_pos 分别指向两个有序子数组的开始位置。
- 比较两个指针指向的元素,将两个有序子数组中较小元素依次存入到结果数组 a 中,并将指针移动到下一位置。
- 重复步骤 3,直到某一指针到达子数组末尾。
- 将另一个子数组中的剩余元素存入到结果数组中。
完整流程如下,建议反复观看容易理解:
👽代码实现
我觉得我的注释还算清晰了噶##
#include <iostream>
using namespace std;
void merge(int a[],int temp[],int left,int mid,int right){ //归并过程
for(int i = 0; i <= right; ++i){
temp[i] = a[i]; //将a数组元素拷贝到辅助数组中
}
int l_pos = left; //未排序左半区第一个元素下标
int r_pos = mid + 1; //未排序右半区第一个元素下标
int pos = left; //临时数组第一个元素下标
while(l_pos <= mid && r_pos <= right){
if(temp[l_pos] <= temp[r_pos]) //左半区第一个元素小于右半区第一个元素
a[pos++] = temp[l_pos++];
else
a[pos++] = temp[r_pos++];
}
while(l_pos <= mid) a[pos++] = temp[l_pos++]; //复制左半区剩余元素
while(r_pos <= right) a[pos++] = temp[r_pos++]; //复制右半区剩余元素
}
void mSort(int a[],int temp[],int left,int right){ //分解过程
if(left < right){
//递归地将当前数组平均分成两半
int mid = (left + right) >> 1; // >>1 等于 /2
mSort(a,temp,left,mid); //左数组分解
mSort(a,temp,mid + 1,right); //右数组分解
merge(a,temp,left,mid,right); //合并
}
}
void MergeSort(int a[],int n){
int *temp = new int[n]; //开辟辅助数组
//c语言 : int *temp = (int*)malloc(n * sizeof(int));
mSort(a,temp,0,n - 1);
delete[] temp; //c语言 : free(temp)
}
void Print(int a[],int n){ //打印数组
for(int i = 0;i < n; ++i){
printf("%d ",a[i]);
}
puts("");
}
int main(){
int a[] = {0,5,7,3,1,6,8,4};
int n = sizeof(a)/sizeof(a[0]); //获取数组长度
Print(a,n);
MergeSort(a,n); //进行归并排序
Print(a,n);
return 0;
}😎性能分析
时间效率:O(nlong₂ⁿ)。
空间效率:O(n),用了辅助数组O(n)。
稳定性:因为在两个有序子数组的归并过程中,如果两个有序数组中出现相等元素,merge算法能够使前一个数组中那个相等元素先被复制,从而确保这两个元素的相对顺序不发生改变。因此,归并排序算法是一种 稳定排序算法。
适用性:适用于顺序存储和链式存储的线性表。
👻题目练习
【题目描述】LCR 170. 交易逆序对的总数 - 力扣(LeetCode)

【解题思路】
用暴力解法一定超时,这里可采用归并排序。
重点在于 [合并过程] ,假设左右区间已经有序,执行合并,当右区间元素加入到原始数组时,计数器加上左区间剩余元素数量作为答案贡献值。因为左区间元素一定小于当前加入元素,刚好与当前元素构成逆序对。当左区间元素加入时,就不进行计数,因为已经算过了。像这样:
利用分治思想,将大问题分解成小问题。每次合并成更大的子数组,为下一次合并做准备,直至合并成有序的数组。
【AC代码】
class Solution {
public:
int reversePairs(vector<int>& record) {
int n = record.size();
vector<int> temp(n); //开一个辅助数组
return MergeSort(record,temp,0,n - 1);
}
int MergeSort(vector<int>& a,vector<int>& temp,int left,int right){
if(left >= right) return 0;
int mid = (left + right) >> 1;
int leftPairs = MergeSort(a,temp,left,mid); //记录左区间的逆序对
int rightPairs = MergeSort(a,temp,mid + 1,right); //记录右区间的逆序对
int totalPairs = MergeAndCount(a,temp,left,mid,right); //记录总的逆序对
return leftPairs + rightPairs + totalPairs; //返回所有的逆序对就是答案
}
int MergeAndCount(vector<int>& a,vector<int>& temp,int left,int mid,int right){
for(int i = left; i <= right; ++i){
temp[i] = a[i];
}
int l_pos = left,r_pos = mid + 1;
int pos = left;
int count = 0; //计数器
while(l_pos <= mid && r_pos <= right){
if(temp[l_pos] <= temp[r_pos]){
a[pos++] = temp[l_pos++];
}else{
a[pos++] = temp[r_pos++];
count += (mid - l_pos + 1); //只有右区间加入元素时统计左区间的元素
}
}
while(l_pos <= mid) a[pos++] = temp[l_pos++];
while(r_pos <= right) a[pos++] = temp[r_pos++];
return count;
}
};桶排序⭐⭐⭐
🧐算法描述
桶排序(Bucket Sort):将待排序数组中的元素分散到若干个「桶」中,然后对每个桶中的元素再进行单独排序。
利用哈希的思想,将元素分类,同一类的映射(哈希)到同一个桶中,每个桶是一个数组,映射完毕以后,对每个桶执行排序(可以是任意排序,比如 快速排序、归并排序 等等)。
💖具体实现
我们 [39,49,8,13,22,15,10,30,5,44]为例,演示一下桶排序算法的整个步骤。
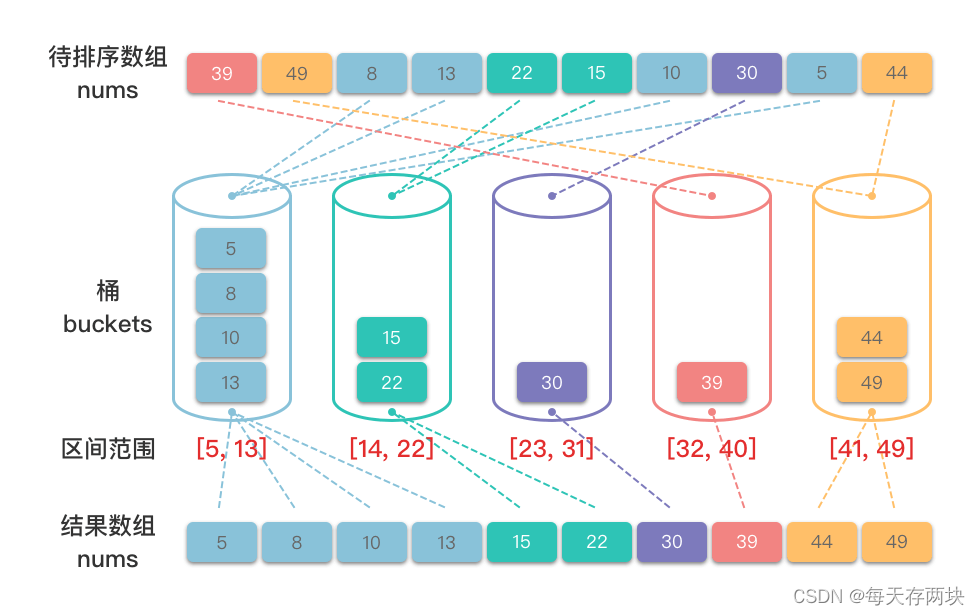
- 确定桶的数量:根据待排序数组的值域范围,将数组划分为 𝑘k 个桶,每个桶可以看做是一个范围区间。
- 分配元素:遍历待排序数组元素,将每个元素根据大小分配到对应的桶中。
- 对每个桶进行排序:对每个非空桶内的元素单独排序。
- 合并桶内元素:将排好序的各个桶中的元素按照区间顺序依次合并起来,形成一个完整的有序数组。
👽代码实现
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// 选择排序
void SelectionSort(vector<int>& nums){
int n = nums.size();
for(int i = 0;i < n - 1; ++i){
int min = i;
for(int j = i + 1; j < n; ++j){
if(nums[j] < nums[min]) min = j;
}
swap(nums[i],nums[min]);
}
}
// 桶排序
vector<int> bucketSort(vector<int>& nums) {
int bucket_size = 5; //定义每个桶的大小
// 计算待排序序列中最大值元素 nums_max、最小值元素 nums_min
int nums_min = *min_element(nums.begin(), nums.end());
int nums_max = *max_element(nums.begin(), nums.end());
// 定义桶的个数为 (最大值元素 - 最小值元素) / 每个桶的大小 + 1
int bucket_count = (nums_max - nums_min) / bucket_size + 1;
// 定义桶数组 buckets
vector<vector<int>> buckets(bucket_count);
// 遍历待排序数组元素,将每个元素根据大小分配到对应的桶中
for (int num : nums) {
buckets[(num - nums_min) / bucket_size].push_back(num);
}
// 对每个非空桶内的元素单独排序,排序之后,按照区间顺序依次合并到 res 数组中
vector<int> res;
for (auto& bucket : buckets) {
SelectionSort(bucket);
res.insert(res.end(), bucket.begin(), bucket.end());
}
return res; // 返回结果数组
}
void Print(vector<int> nums){ //打印数组
for(int x : nums){
printf("%d ",x);
}
puts(" ");
}
int main() {
vector<int> arr = {29,25,3,49,9,37,21,43}; // 待排序数组
Print(arr);
vector<int> sortedArr = bucketSort(arr); // 调用桶排序
Print(sortedArr);
return 0;
}
😎性能分析
时间效率:时间复杂度接近于 O(n)。
空间效率:O(n+m)。由于桶排序使用了辅助空间,所以桶排序的空间复杂度是 O(n+m)。
稳定性:排序的稳定性取决于桶内使用的排序算法。如果桶内使用稳定的排序算法(比如插入排序算法),并且在合并桶的过程中保持相等元素的相对顺序不变,则桶排序是一种 稳定排序算法。反之,则桶排序是一种 不稳定排序算法。
适用性:顺序存储的线性表。
👻题目练习
【题目描述】220. 存在重复元素 III - 力扣(LeetCode)

【解题思路】
此题用暴力也一样会超时,可以利用桶排序的思想解决此问题
我们可以首先创建一个桶数组,然后遍历数组 nums,将每个元素放入对应的桶中。接着,我们遍历桶数组,对于每个非空的桶,我们可以检查与其相邻的桶内的元素是否满足条件。
并不断地更新桶的内容,同时根据
indexDiff的要求适时删除旧的桶项,确保每个时刻桶中保存的信息都是与当前元素相关的、可能形成有效元素对的候选。这种方式隐含了对所有可能的i和j组合的检查,避免了双重循环,大大提高了效率。
【AC代码】
class Solution {
using ll = long long;
public:
bool containsNearbyAlmostDuplicate(vector<int>& nums, int indexDiff, int valueDiff) {
if (indexDiff <= 0 || valueDiff < 0) return false;
unordered_map<ll, ll> bucket; //用哈希表来存储桶信息
ll Size = (ll)valueDiff + 1; //定义桶大小
for (int i = 0; i < nums.size(); ++i) {
ll x = nums[i];
ll idx = (x - INT_MIN) / Size; //确保当前数的索引为正数
if (bucket.count(idx) > 0) return true; //对应桶中存在说明满足条件
//检查相邻的桶中是否满足条件
if (bucket.count(idx - 1) > 0 && abs(bucket[idx - 1] - x) <= valueDiff)
return true;
if (bucket.count(idx + 1) > 0 && abs(bucket[idx + 1] - x) <= valueDiff)
return true;
bucket[idx] = x; //插入桶中
if (i >= indexDiff)
bucket.erase(((ll)nums[i - indexDiff] - INT_MIN) / Size); //索引超出直接从桶中删去
}
return false;
}
};计数排序⭐⭐
🧐算法描述
计数排序(Counting Sort):是一个非基于比较的稳定的线性时间的排序算法,通过统计数组中每个元素在数组中出现的次数,根据这些统计信息将数组元素有序的放置到正确位置,从而达到排序的目的。
计数排序的名字会让我们想到“计数法”,实际上计数排序的实现就是使用的计数法。




💖具体实现
我们以 [3,0,4,2,5,1,3,1,4,5] 为例,演示一下计数排序算法的整个步骤。
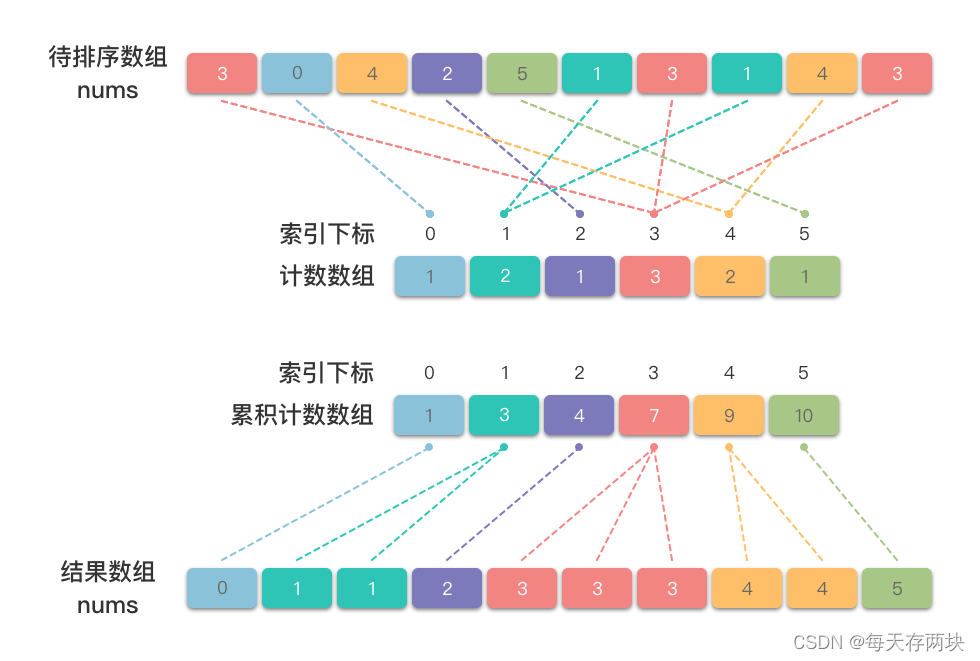
- 使用一个额外的数组 cnt,其中第 i 个元素是待排序数组 nums 中值等于 i 的元素的个数,然后根据数组 cnt 来将 nums 中的元素排到正确的位置。
- 创建一个足够大的数组 cnt,足够大的意思是 cnt 的下标范围可以包括所有的待排序数据值。然后遍历待排序数据,使用计数法统计每个数据的出现次数。最后遍历 cnt 数组,将每一个值(cnt[i])不为 0 的下标(i)放入原数组 cnt[i] 次。
👽代码实现
#include <iostream>
#include <vector>
using namespace std;
void CountingSort(int nums[], int n) {
int maxNum = 0;
for (int i = 0; i < n; ++i) {
maxNum = max(maxNum, nums[i]);
}
vector<int> cnt(maxNum,0); // 计数器初始化为全 0
int top = 0;
for (int i = 0; i < n; ++i) cnt[nums[i]]++; //元素在计数器中加一
for (int i = 0; i <= maxNum; ++i) {
while (cnt[i] != 0) {
nums[top++] = i;
--cnt[i];
}
}
}
void Print(int nums[], int n) { //打印数组
for (int i = 0; i < n; ++i) printf("%d ", nums[i]);
puts("");
}
int main() {
int nums[] = {3, 0, 4, 2, 5, 1, 3, 1, 4, 5};
int n = sizeof(nums) / sizeof(nums[0]); //获取数组长度
Print(nums, n);
CountingSort(nums, n); //进行计数排序
Print(nums, n);
}
😎性能分析
时间效率:O(n+k)。其中 k 代表待排序数组的值域。
空间效率:O(k)。其中 k 代表待排序序列的值域。由于用于计数的数组 cnt 的长度取决于待排序数组中数据的范围(大小等于待排序数组最大值减去最小值再加 1)。所以计数排序算法对于数据范围很大的数组,需要大量的内存。
稳定性:由于向结果数组中填充元素时使用的是逆序遍历,可以避免改变相等元素之间的相对顺序。因此,计数排序是一种 稳定排序算法
适用性:计数排序一般用于整数排序,不适用于按字母顺序、人名顺序排序。
👻题目练习
【题目描述】1122. 数组的相对排序 - 力扣(LeetCode)

【解题思路】
利用计数排序的思想,将arr1映射到计数器中,在遍历arr2按此顺序添加答案,并将计数器置0,对于arr2没有出现的数,最后需要重新遍历计数器将其加入答案。
【AC代码】
class Solution {
public:
vector<int> relativeSortArray(vector<int>& arr1, vector<int>& arr2) {
int maxNum = 0;
for (int i = 0; i < arr1.size(); ++i)
maxNum = max(maxNum, arr1[i]);
vector<int> cnt(maxNum + 1,0); //定义计数器
vector<int> ans;
for(int x : arr1) cnt[x]++;
for(int x : arr2){
for(int i = 0; i < cnt[x]; ++i){
ans.push_back(x);
}
cnt[x] = 0; //加完将计数器置0
}
for(int i = 0; i < cnt.size(); ++i){ //最后将遗漏元素加入答案
while(cnt[i] != 0){
ans.push_back(i);
--cnt[i];
}
}
return ans;
}
};基数排序⭐⭐⭐⭐
🧐算法描述
基数排序(Radix Sort):将整数按位数切割成不同的数字,然后从低位开始,依次到高位,逐位进行排序,从而达到排序的目的。
基数排序本质也是桶排序,不过它是利用数位来划分桶。
💖具体实现
我们以 [692,924,969,503,871,704,542,436]为例,演示一下基数排序算法的整个步骤。
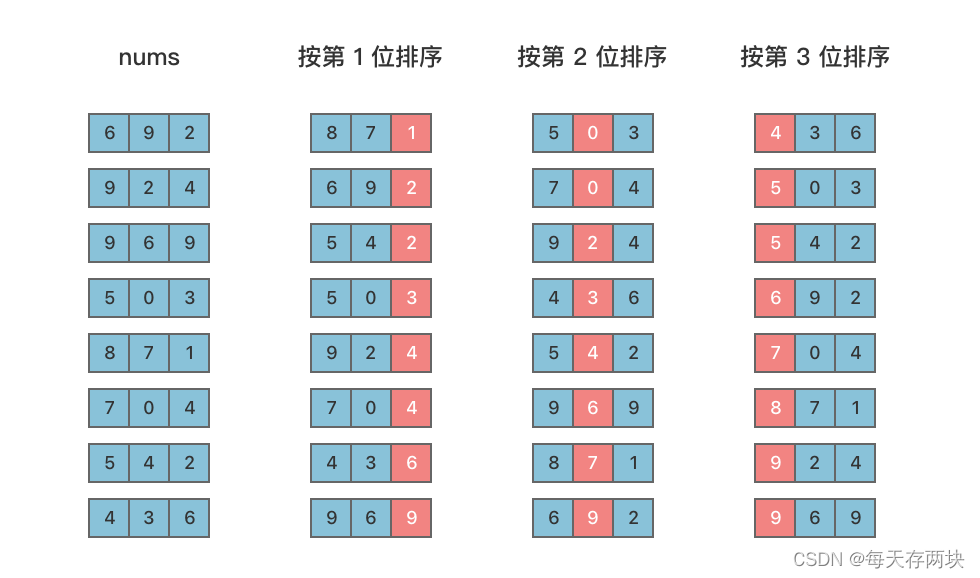
首先,准备 10 个队列(一种 「 先进先出 」 的数据结构),进行若干次「 迭代 」。每次「 迭代 」,先清空队列,然后取每个待排序数的对应十进制位,通过「 哈希 」映射到它「 对应的队列 」中,然后将所有数字「 按照队列顺序 」塞回「 原数组 」完成一次 「 迭代 」。
在进行排序过程中,我们需要取得一个数字 v 的十进制的第 k 位的值。如下
我们要得到的就是 ak。
可以将 v 直接除上 10ᵏ 再模上 10,即 v / 10ᵏ mod 10 。
例如:2024 取十位,v / 10¹ mod 10 = 2024 / 10 % 10 = 2。
- 定好进制位exp,一般从个位1开始。
- 初始化 10个队列,将所有数字按照当前位的数值放入对应的队列中。
- 从第 0 个队列到 第 9 个队列,将所有数字按照顺序取出来,放回原数组。
- 更新进制位exp,从低位到高位,然后继续迭代。

👽代码实现
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
void radixSort(vector<int>& nums) {
int maxVal = *max_element(nums.begin(), nums.end());//获取数组中的最大数,用于确定排序的轮数
int exp = 1; //初始化为1,表示个位
queue<int> buckets[10]; // 10个队列,分别存放0-9的数字
while(maxVal / exp > 0) {
// 将所有数字按照当前位的数值放入对应的队列中
for(int x : nums) {
int idx = (x / exp) % 10; //哈希映射
buckets[idx].push(x);
}
// 从队列中取出元素,放回原数组,准备下一轮排序
int pos = 0;
for(int i = 0; i < 10; i++) {
while( !buckets[i].empty() ) {
nums[pos++] = buckets[i].front();
buckets[i].pop();
}
}
exp *= 10; // 指数增倍,进行更高位的排序
}
}
void Print(vector<int> nums) { // 打印数组
for(const int x : nums) {
cout << x << " ";
}
cout << endl;
}
int main() {
vector<int> nums = {692,924,969,503,871,704,542,436};
Print(nums);
radixSort(nums); //进行基数排序
Print(nums);
return 0;
}😎性能分析
时间效率:O(n×k)。其中 n 是待排序元素的个数,k 是数字位数。k 的大小取决于数字位的选择(十进制位、二进制位)和待排序元素所属数据类型全集的大小。
空间效率:O(n+k)。
稳定性:基数排序采用的桶排序是稳定的。基数排序是一种 稳定排序算法。
适用性:基数排序适用于顺序存储和链式存储
引申:如果待排序数组中有负数,那么基数排序又该如何如何实现呢。
可以加一个偏移量,偏移所有数使其非负。
👻题目练习
【题目描述】164. 最大间距 - 力扣(LeetCode)

【解题思路】
题目要求在线性时间复杂度O(n)内解决,前面的快速排序,归并排序的复杂度达到O(nlong₂ⁿ)。所以这里可以采取基数排序,然后遍历数组找到相邻最大元素即可。
【AC代码】
class Solution {
public:
int maximumGap(vector<int>& nums) {
int n = nums.size();
if(n < 2) return 0;
int maxVal = *max_element(nums.begin(),nums.end());
queue<int> buckets[10];
int exp = 1;
while(maxVal / exp > 0){
for(int num : nums){
int idx = (num / exp) % 10;
buckets[idx].push(num);
}
int pos = 0;
for(int i = 0; i < 10; ++i){
while( !buckets[i].empty() ){
nums[pos++] = buckets[i].front();
buckets[i].pop();
}
}
exp *= 10;
}
int ans = 0;
for(int i = 1; i < n; ++i){
ans = max(nums[i] - nums[i - 1],ans);
}
return ans;
}
};
总结
做好小事,熬过难事,静成大事。每天学习一点,进步一点,好好珍惜现在的学习时光。
最后祝你我在这声色牛马的世界里保持清澈。