一. 选择排序

1.1 选择排序的实现思路

1.2 选择排序函数代码

1.3 选择排序的时间复杂度分析

二. 堆排序

2.1 堆排序的实现思路

2.2 堆排序函数代码

2.3 堆排序的时间复杂度分析

三. 冒泡排序

3.1 冒泡排序的基本思想

3.2 冒泡排序函数代码

3.3 冒泡排序的时间复杂度分析

前置说明：本文中所有排序算法均以排升序为例进行讲解。

一. 选择排序

1.1 选择排序的实现思路

选择排序，就是在一组数据中通过选出最大值（最小值的方法进行排序），假设要对具有n个数据的数组arr中的数据进行排序，具体实现步骤为：

取整个数组中的数据为一数据集，设begin = 0为头部数据下标，end = n - 1为尾部数据的下标，在数据集中找出最大的数据和最小的数据，排升序，最大的数据与尾部数据交换，最小的数据与头部数据交换。
经过上步，头部数据为数组中的最小值，尾部数组为数组中的最大值。取此时数组中的第2个数据到第n-1个数据为一数据集，设begin = 1为头部数据下标，end = n - 2为尾部数据的下标，最大的数据与尾部数据交换，最小的数据与头部数据交换。
重复进行步骤2，直到begin >= end时终止。

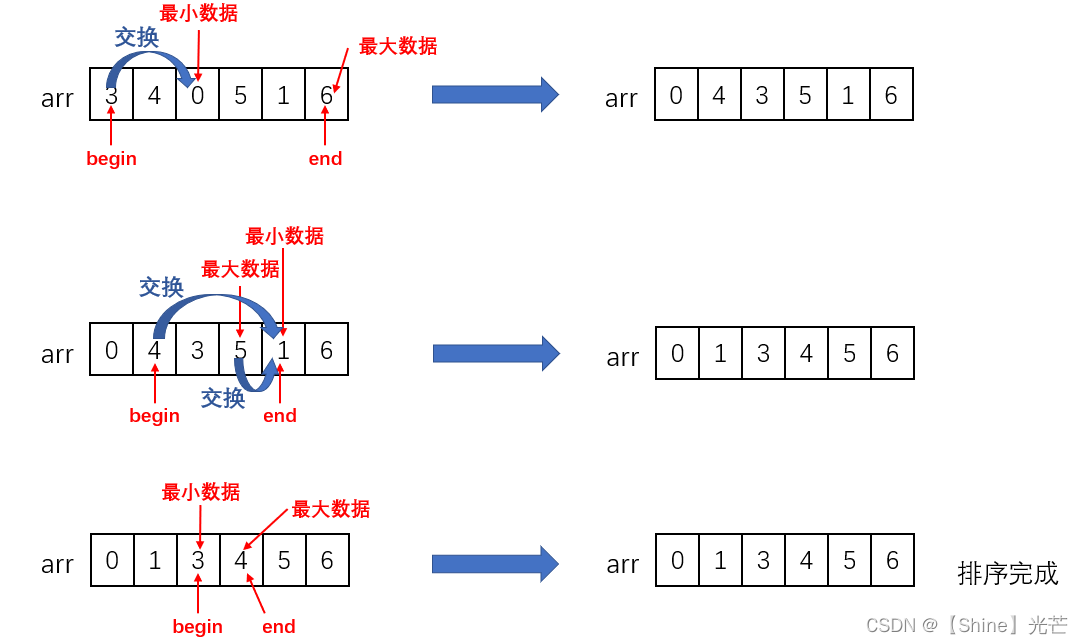
如，对arr[6] = {3,4,0,5,1,6}排升序的过程为：

begin = 0，end = 5，数据集为：{3,4,0,5,1,6}，最大为6，最小为0，arr[6]={0,4,3,5,1,6}。
begin = 1，end = 4，数据集：{4,3,1,5}，最大为4，最小为1，arr[6] = {0,1,3,4,5,6}。
begin = 2，end = 3，数据集：{3,4}，最大为4，最小为3，arr[6] = {0,1,3,4,5,6}。
begin = 3，end = 4，排序完成。

1.2 选择排序函数代码

//数据交换函数
void swap(int* px, int* py)
{
	int tmp = *px;
	*px = *py;
	*py = tmp;
}

//选择排序函数
//参数a为指向存储待排序数组首元素的指针，n为待排序元素的个数
void SelectSort(int* a, int n)
{
	//选择排序
	//每次筛选出未排序数据中最大和最小的那个，存在数组的前部和后部
	int begin = 0;  //前部数据下标
	int end = n - 1;  //后部数据下标

	while (begin < end)
	{
		int mini = begin;   //初始化最小的数据的下标
		int maxi = begin;   //初始化最大的数据的下标

		int i = 0;  //循环参数
		//for循环遍历每一个数据，找出最大的数据和最小的数据的下标
		for (i = begin + 1; i <= end; ++i)
		{
			if (a[i] > a[maxi])
			{
				maxi = i;
			}

			if (a[i] < a[mini])
			{
				mini = i;
			}
		}

		//将最小的数据放在队首，队首数据放在原最小数据位置处
		//将最大的数据放在队尾，队尾数据放在原最大数据位置处
		swap(&a[begin], &a[mini]);
		if (maxi == begin)
		{
			//如果首元素是最大的元素，那么swap(&a[begin], &a[mini])使队首数据不再是最大的数据
			//此时最大的数据被换到下标为mini的位置，更新maxi为mini
			maxi = mini;
		}
		swap(&a[end], &a[maxi]);

		--end;
		++begin;
	}
}

1.3 选择排序的时间复杂度分析

假设要对n个数据进行选择排序，总共要进行n/2次最大值最小值筛选操作，第一次筛选要遍历n个数据，第二次筛选要遍历n-2个数据，...，最后一次筛选要遍历2个数据或3个数据，设遍历一个数据就表示进行一次操作，总共要进行的操作次数为（假设最后一次遍历2个数据）：

$F(N) = N + (N-2)+(N-4) +...+4+2=\frac{1}{2}N^2+N$

根据大O渐进法规则，选择排序的时间复杂度为 $O(N^2)$ 。

注：当待排序数据为偶数个时，最后一次筛选要遍历2个数据，当待排序数据为奇数个时，最后一次筛选要遍历3个数据。

二. 堆排序

2.1 堆排序的实现思路

首先，要明确对于排升序和排降序，应该建大堆还是小堆，记住结论：

排升序，建大堆
排降序，建小堆

堆排序的操作流程如下（排升序）：

建大堆，这里不再新开辟空间来建堆，而是将给定数据的数据顺序调整为满足大堆结构的排列。采用向下调整的方法来进行数据调整，从最后一个非叶子节点（度不为0的节点）开始向下调整，调整到根节点结束，此时数据的排列顺序已满足大堆的结构要求。
交换首尾节点的数据值，此时末尾节点为堆中的最大数据。
将末尾的节点排除出堆，从根节点开始，对堆进行向下调整操作。
重复步骤2和步骤3，直到堆中仅剩一个数据为止。

2.2 堆排序函数代码

//数据交换函数
void swap(DataType* px, DataType* py)
{
	int tmp = *px;
	*px = *py;
	*py = tmp;
}
 
//向下调整函数
//a为存储待排序数据的数组，n为待排序数据的个数
void Adjustdown(DataType* a, int n, int parent)
{
	assert(a);
	int child = 2 * parent + 1;
	while (child < n)
	{
		if (child + 1 < n && a[child] < a[child + 1])
			++child;
 
		if (a[parent] < a[child])
		{
			swap(&a[parent], &a[child]);
			parent = child;
			child = 2 * parent + 1;
		}
		else
		{
			break;
		}
	}
}
 
//堆排序函数（升序）
void HeapSort(DataType* a, int n)
{
	assert(a);
 
	//先采用向下调整的方式将a中的数据建立为大堆
	//从后往前调整，叶子节点不用单独调整
	//因此，从第一个度不为0的节点开始往前调整到第一个节点即可
	int end = (n - 1 - 1) / 2;
	while(end >= 0)
	{
		Adjustdown(a, n, end);
		--end;
	}
 
	//将a排为大堆后
	//将a的数据首尾交换，排除最后一个节点，将堆进行向下调整
	//重复进行上述操作n-1次，堆（数组）中的数据变为升序
	end = n - 1;
	while (end)
	{
		swap(&a[0], &a[end]);
		Adjustdown(a, end, 0);
		--end;
	}
}

2.3 堆排序的时间复杂度分析

对N个数据进行堆排序，要先后进行建堆操作和向下调整操作。

建堆操作的时间复杂度

在堆排序中，采用向下调整的方法进行建堆。从倒数第二层开始将每个节点向下调整，假设层数为h，倒数第二层最多进行下调1次下调操作，倒数第三层最多进行2次下调操作，...，第二层最多进行h-2次下调操作，第一层最多进行h-1次下调操作，每层节点数和层数的关系为： $n = 2^{h-1}$ ， $n$ 为第 $h$ 层节点数。综上，通过向下调整建堆要进行调整的次数最多为：

$F(N)=2^{h-2}\times 1+2^{h-3}\times2+2^{h-4}\times3...+2^1\times (h-2)+2^0\times(h-1)$ （1）

$2\times F(N)=2^{h-1}\times 1+2^{h-2}\times 2+2^{h-3}\times3+....+2^2\times(h-2)+2^1\times(h-1)$ （2）

（2）-（1）得：

$F(N)=2^{h-1} +2^{h-2}+2^1-h+1=\frac{2-2^{h}}{1-2}-h+1=2^{h}-h-1$

根据二叉树结构的性质： $N=2^h-1$ ， $h=log(N+1)$

因此： $F(N)=N-log(N+1)$ 。

根据大O渐进法，建堆操作的时间复杂度为： $O(N)$ 。

向下调整的时间复杂度

堆排序的基本思想是在建立堆之后交换首尾节点数据，然后向下调整根节点数据来实现的，假设堆中共有N个数据，总共要对N-1个数据向下调整，设二叉树的层数为h，每次向下调整最多调整h-1次，总共进行的向下调整操作的最多次数为：

$F(N)=(N-1)\times h = (N-1)log(N+1)$

根据大O渐进法，堆排序中调整过程的时间复杂度为： $O(NlogN)$ 。

整个堆排序的时间复杂度

整个堆排序要进行建堆操作和向下调整操作，时间复杂度记 $O(N+NlogN)$ ，根据大O渐进法规则，堆排序时间复杂度可表示为： $O(NlogN)$ 。

三. 冒泡排序

3.1 冒泡排序的基本思想

冒泡排序的基本思想是交换，通过相邻两数的交换，达到排升序（降序）的目的，给定含有n个数据的数组arr，对arr中的数据排升序的操作步骤为：

从arr中的第二个数据开始到最后一个数据，每个数据与它前面的那个数据进行比较，如果前面的数据大于后面的数据，则交换两个数据，经过这一趟排序，数组中最后面的数为最大的数据。
从数组中第二个数据开始到倒数第二个数据，每个数据与它前面的那个数据进行比较，如果前面的数据大于后面的数据，则交换两个数据，此时数组中最后一个数据和倒数第二个数据分别为最大的数据和次大的数据。
重复步骤1和2，直到完成排序。

图3.1展示了对数组arr[6] = {6,5,4,3,2,1}的第一趟排序的实现过程，经过一趟排序，arr中最大的值到了最后面的位置，第二趟排序对arr中的前5个数据进行相同的操作即可，第二趟排序结束后arr应当变为arr[6]={4,3,2,1,5,6}。

冒泡排序的优化：

设想，如果单趟排序未发生数据交换，那就表示数据已经有序，数据有序就可以终止循环。因此，可以定义一个变量exchange来表示单趟排序是否发生数据交换，可以取exchange=1表示发生了数据交换，exchange=0表示没发生数据交换，每结束一次单趟循环都对exchange的值进行检查，如果exchange==0成立，则排序终止。

3.2 冒泡排序函数代码

//冒泡排序函数
void bubbleSort(int* a, int n)
{
	int i = 0;  //循环参数，表示冒泡排序趟数
	int j = 0;  //循环参数，表示下标

	for (i = 0; i < n - 1; ++i) //单趟排序
	{
		int exchange = 0;   //数据交换标识符，如果单趟排序发生数据交换为1，否则为0
		for (j = 0; j < n - 1 - i; ++j)
		{
			//排升序，如果前面的数大于后面则交换
			if (a[j] > a[j + 1])
			{
				exchange = 1;
				int tmp = a[j];
				a[j] = a[j + 1];
				a[j + 1] = tmp;
			}
		}

		//如果单趟排序未发生数据交换flag=0，则表示数据已经有序，终止排序即可
		if (0 == exchange)
		{
			break;
		}
	}
}