连载文章,长期更新,欢迎关注:
下面将从原理分析、源码解读和安装与运行这3个方面展开讲解LSD-SLAM算法。
9.2.1 LSD-SLAM原理分析
前面已经说过,LSD-SLAM算法是直接法的典型代表。因此在下面的分析中,首先介绍一下直接法的基本原理,然后合论文[6,7,8]对LSD-SLAM系统框架展开具体分析。
1.直接法
其实不管是特征点法还是直接法,都是利用图像之间的共视关系建立数据关联,然后求解相机位姿变换和地图云点的过程。在特征点法中,先从图像像素点中提取一些比较独特的点(即特征点),然后在不同视角拍摄的图像中寻找特征点的匹配关系,接着将这些匹配好的特征点用来构建共视关系计算模型求出机位姿和环境地图点。而在直接法中,直接将图像中的每个像素点放入某种计算模型中参与计算,通过这种由像素点直接参与计算的共视关系计算模型就能求出机位姿和环境地图点。下面通过特征点法与直接法的对比讨论,帮助大家更进一步理解直接法。
对于特征点法来说,首先对给定的两帧图像分别进行特征提取和特征匹配,然后根据不同的已知条件构建相应模型求解相机位姿和地图云点。在单目SLAM初始化阶段仅已知两帧图像及其匹配关系,那么就是2D-2D模型,利用对极约束或者单应约束求出相机位姿变换,然后再利用三角化重建地图云点。在单目SLAM初始化完成后就能得到一些已知地图点或者双目、RGB-D能直接给出环境观测点时,就已知两帧图像、匹配关系和地图云点,那么就是3D-2D模型,利用各种PnP算法求出相机位姿变换,一旦当前相机位姿已知,双目或RGB-D由于深度信息已知可以直接重建地图云点,单目的话则依然用三角化重建地图云点。在双目或RGB-D能直接获取深度信息时,在已知两帧图像及其匹配关系后,其实两帧图像各自观测的地图云点及其匹配关系也就知道了,那么就是3D-3D模型,利用ICP算法求出相机位姿变换,一旦当前相机位姿已知,双目或RGB-D由于深度信息已知可以直接重建地图云点。不管是2D-2D、3D-2D还是3D-3D,都能求出相机位姿变换和地图云点,这可以当成初始值,然后利用最小化重投影误差来优化相机变换和地图云点或者仅优化相机位姿变换。
对于直接法来说,不进行特征提取和特征匹配,直接用图像像素建立数据关联,通过最小化光度误差件构建相应模型求解相机位姿和地图云点。在单目情况下深度信息未知,最小化光度误差过程需要同时对相机位姿变换和地图云点深度信息进行估计。在双目或RGB-D情况下深度信息已知,最小化光度误差过程对相机位姿变换进行估计会简单很多,而地图云点可以直接重建出来。因为直接法是在图像像素上通过深度估计来重建地图云点,如果将图像中的每个像素都进行深度估计然后重建出地图云点,那么构建出来的就是稠密地图;如果只对图像中的部分像素(比如梯度较大的像素)进行深度估计然后重建出地图云点,那么构建出来的就是半稠密地图或者稀疏地图。
(1)重投影误差与光度误差对比分析
先来讨论重投影误差,如图9-47a所示。假如第帧图像中的像素点
与第
帧图像中的像素点
通过特征匹配建立了关联,也就是说环境中的同一个三维点
投影到第
帧图像和第
帧图像分别得到像素点
和
。假设
在第
帧相机坐标系
的坐标为
,而
在第
帧相机坐标系
的坐标为
。那么环境点
与像素点
的投影关系,如式(9-49)所示。而像素点
到环境点
的反投影关系,如式(9-50)所示。
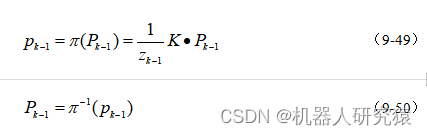
而坐标系中的点
坐标值通过
可以变换为坐标系
中的点
坐标值表示,而点
重投影回第
帧图像得到像素点
,如式(9-51)和(9-52)所示。
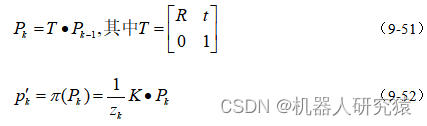
如果相机位姿变换不存在误差且相机投影过程不存在噪声干扰,那么重投影得到的像素点
与实际观测得到的像素点
在像素坐标上应该重合。正是由于机位姿变换
误差和相机投影过程噪声干扰的存在,使得重投影像素点
与实际观测像素点
并不重合,两者之间像素坐标的相差距离就是所谓的重投影误差,如式(9-53)所示。
![]()
上面只是讨论了一个特征点的重投影误差,考虑所有特征点的重投影误差,就可以通过最小化重投影误差来优化相机位姿变换和地图云点,如式(9-54)所示。

而光度误差,如图9-47b所示。对于第帧图像中的任意像素点
反投影到环境三维点
,同样假设
在第
帧相机坐标系
的坐标为
,而
在第
帧相机坐标系
的坐标为
。同样,用式(9-51)和(9-52)重投影得到像素点
。如果相机位姿变换
不存在误差且相机投影过程不存在噪声干扰,并假设环境中的同一个物体点投影到不同的相机形成的像素灰度值是一样的(即光度不变假设),那么
投影到第
帧图像形成的像素灰度值
与
重投影到第
帧图像形成的像素灰度值
应该是相等的。正是由于机位姿变换
误差和相机投影过程噪声干扰的存在,使得
与
不相等,这两个灰度值之差就是所谓的光度误差,如式(9-55)所示。

上面只是讨论了一个像素点的光度误差,考虑所有像素点的光度误差,就可以通过最小化光度误差来优化相机位姿变换和地图云点,如式(9-56)所示。
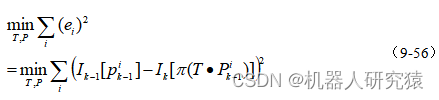
不难发现在计算重投影误差时,需要借助特征匹配,然后在同一幅图像中计算两个像素点之间的坐标距离。而在计算光度误差时,并不需要特征匹配,对于任意像素点都可以计算一幅图像中像素点灰度值与重投影到另一幅图像中像素点灰度值的差值。
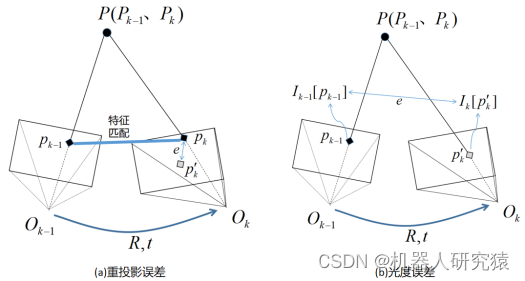
图9-47 重投影误差与光度误差
(2)特征点法与直接法优缺点分析
对于特征点法,借助特征提取和特征匹配建立强数据关联,使得参与计算的数据模型具有很高的鲁棒性,系统不易受干扰;由于特征点数量稀疏,能使优化问题控制在较小的规模。而辩证的角度看,特征点的优点也是其缺点。在特征提取和特征匹配时,计算耗时很大,是制约系统速度提升的重要环节;对于具有几十万甚至上百万像素点的图像,仅仅提取百十来个特征点用于计算,图像中其他大量的有用信息白白被丢弃了,一旦特征缺失、图像模糊、误匹配等情况发生,计算模型将立即失效。
而直接法与特征点法正好互补,对于直接法来说不需要特征提取和特征匹配,而是让像素点直接参与计算,既节省了特征提取和特征匹配消耗的时间,又保留了图像中所有像素点携带的巨大信息量,在特征缺失、图像模糊、图像出现噪点时依然能保持工作。虽然直接法并不在特提取和特征匹配上消耗计算时间,但是由于参与计算的像素点数量巨大,造成优化问题规模较大;另外直接法基于光度不变假设,这显然是一个强假设,实际情况往往不成立。
2.LSD-SLAM系统框架
到这里就可以分析LSD-SLAM的系统框架了,结合算法原作者清晰的论文思路[6,7,8],很容易理解整个算法的组成架构。由于LSD-SLAM支持单目、双目和全景这3种相机,所以系统框架也分3种情况来讨论。单目系统架构由3部分构成,即追踪(Tracking)、深度估计(Depth Map Estimation)和地图优化(Map Optimization),如图9-48所示。
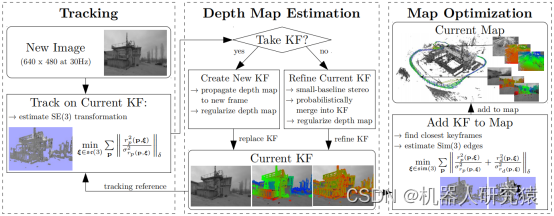
图9-48 单目系统框架
双目系统架构,如图9-49所示。相比于单目系统,双目能直接获取图像的深度信息,这样系统尺度不确定性消失了,深度估计也更容易进行。
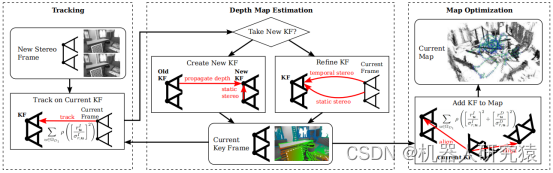
图9-49 双目系统框架
全景系统架构,如图9-50所示。全景系统中采用广角或者鱼眼镜头的相机获取图像,这样可以获取接近180°视角内更丰富的图像信息。相比于针孔模型的普通单目相机,全景相机的镜头对光有更强的折射能力,导致图像在成像平面上会有较大的畸变。在实际应用中,可以建立一个映射模型将全景相机的畸变图像转换成非畸变图像。
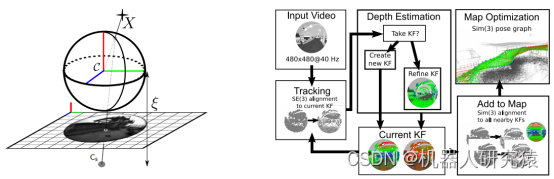
图9-50 全景系统框架
由于双目和全景系统架构是从单目系统架构发展而来,也就是说掌握了单目系统的原理,理解双目和全景系统非常容易,所以下面就以单目系统的原理展开进一步的分析。
(1)地图结构
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
(2)追踪
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
(3)深度估计
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
(4)地图优化
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
9.2.2 LSD-SLAM源码解读
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
9.2.3 LSD-SLAM安装与运行
(先占个坑,有时间再来补充详细内容,大家可以直接看文后的参考文献)
参考文献
【1】 张虎,机器人SLAM导航核心技术与实战[M]. 机械工业出版社,2022.