PDF文档公众号回复关键字:20240610

2023 CSP-J 选择题
单项选择题（共15题，每题2分，共计30分：每题有且仅有一个正确选项）

11 给定一棵二叉树，其前序遍历结果为：ABDECFG，中序遍历结果为：DEBACFG。请问这棵树的正确后序遍历结果是什么？（ ）

A EDBGFCA

B EDBGCFA

C DEBGFCA

D DBEGFCA

12 考虑一个有向无环图，该图包括4条有向边：(1,2)，(1,3)，(2,4)，和(3,4)。以下哪个选项是这个有向无环图的一个有效的拓扑排序？（ ）

A 4，2，3，1

B 1，2，3，4

C 1，2，4，3

D 2，1，3，4

2 相关知识点

1) 树

线性结构(数组、链表等)中节点是首位相接一对一关系，在树结构中节点之间不再是简单的一对一关系，而是较为复杂的一对多的关系

数据结构中的 树 的名字由来，是因为如果把节点之间的关系直观展示出来，由于长得和现实世界中的树很像，由此得名

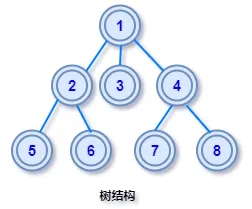
2) 二叉树

每个结点至多拥有两棵子树(即二叉树中不存在度大于2的结点)，并且，二叉树的子树有左右之分，其次序不能任意颠倒

例如下面是一棵二叉树

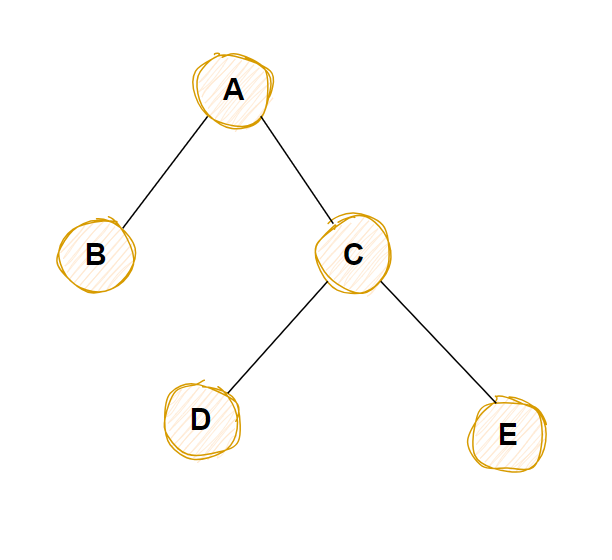
3) 二叉树的遍历

常见的二叉树的遍历主要有3种，先序遍历，中序遍历，后序遍历

先序遍历

先序遍历又叫先根遍历，遍历的顺序为根，左孩子，右孩子

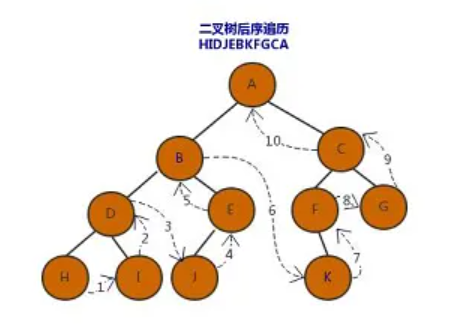
下面二叉树的前序遍历顺序为 ABDHIEJCFKG

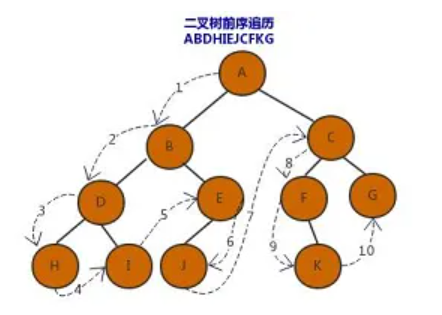
中序遍历

中序遍历又叫中根遍历，遍历的顺序为左孩子，根，右孩子

下面二叉树的中序遍历顺序为 HDIBJEAFKCG

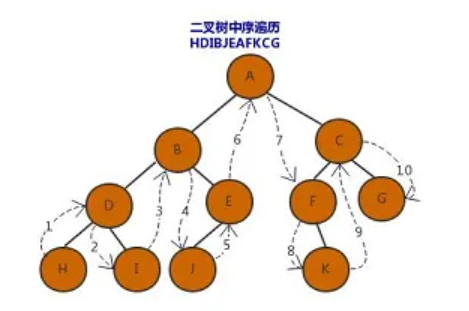
后序遍历

后序遍历又叫后根遍历，遍历的顺序为左孩子，右孩子，根

下面二叉树的后序遍历顺序为 HIDJEBKFGCA

4) 拓扑排序

有向无环图

有向无环图，DAG(Directed Acyclic Graph),若一个有向图中不存在环，则称为有向无环图

拓扑排序

拓扑排序是一个有向无环图（DAG）的所有顶点的线性序列

每个顶点只能出现一次，如果A到B节点有路径，且A节点在B节点的前面，那么B节点不能在A节点的前面

下图是一个有向无环图

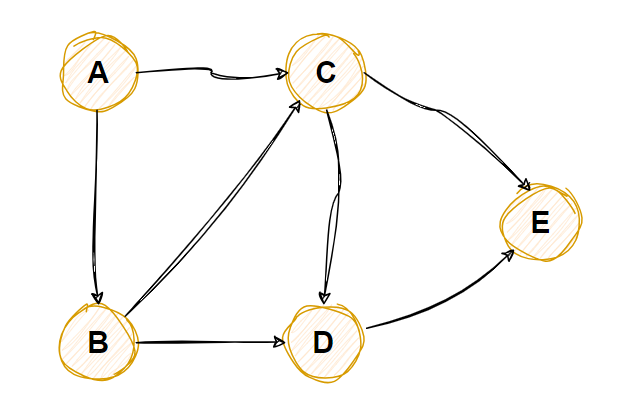
拓扑排序方法

1从 DAG 图中选择入度为0的顶点（即没有节点指向该节点）并输出，并删除此节点
上图中A符合
输出A 并删除A后，变成下图

2从 DAG 图中选择入度为0的顶点（即没有节点指向该节点）并输出，并删除此节点
上图中B符合
输出B 并删除B后，变成下图

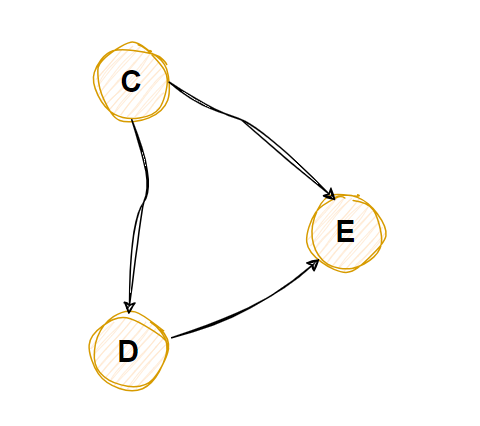
3从 DAG 图中选择入度为0的顶点（即没有节点指向该节点）并输出，并删除此节点
上图中C符合
输出C 并删除C后，变成下图

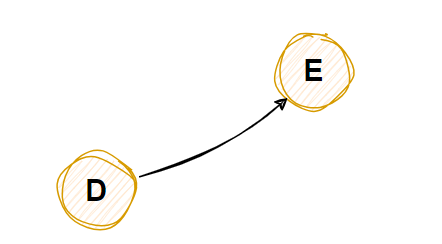
4从 DAG 图中选择入度为0的顶点（即没有节点指向该节点）并输出，并删除此节点
上图中D符合
输出D 并删除D后，只剩下节点E，此时输出节点E

所以上图拓扑排序为ABCDE

3 思路分析

11 给定一棵二叉树，其前序遍历结果为：ABDECFG，中序遍历结果为：DEBACFG。请问这棵树的正确后序遍历结果是什么？（ ）

A EDBGFCA

B EDBGCFA

C DEBGFCA

D DBEGFCA

答案 A

分析

构造二叉树

1 由前序遍历A是根节点，中序遍历通过A分左右子树DEB和CFG

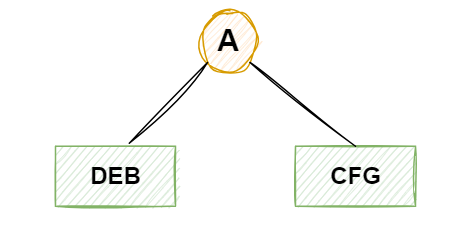
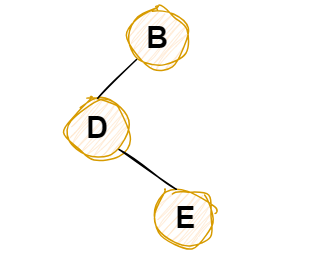
2 中序遍历DEB中在前序遍历BDE，其中DB和DB顺序是反的，所以D是B的左孩子
  前序遍历DE和中序遍历都是DE，所以E是D的右孩子

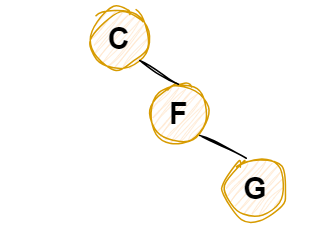
3 中序遍历CFG中在前序遍历也是CFG，其中CF在前序遍历和中序遍历顺序相同，所以F是C的右孩子
  前序遍历FG和中序遍历都是FG，所以G是F的右孩子

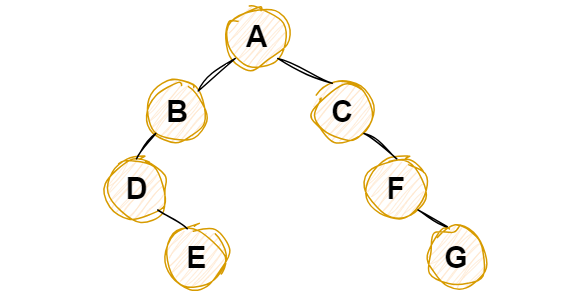
4 所以构造整棵二叉树如下
  所以后续遍历为 EDBGFCA

12 考虑一个有向无环图，该图包括4条有向边：(1,2)，(1,3)，(2,4)，和(3,4)。以下哪个选项是这个有向无环图的一个有效的拓扑排序？（ ）

A 4，2，3，1

B 1，2，3，4

C 1，2，4，3

D 2，1，3，4

答案 B

分析

1 根据边构造有向无环图

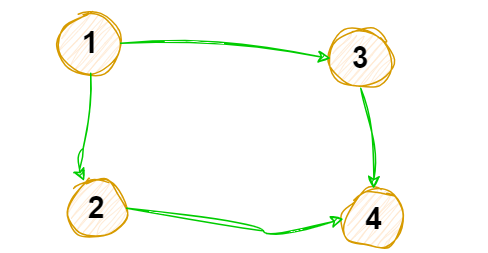
2 输出入度为0的节点，并删除入度为0的节点和此节点对应连线
  入度为0的节点为1，输出1，并删1节点和1节点对应连线
  删除后如下图

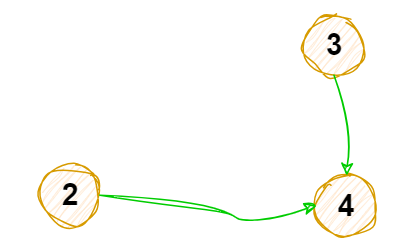
3 输出入度为0的节点，并删除入度为0的节点和此节点对应连线
  入度为0的节点为2或3，选择输出2，并删2节点和2节点对应连线
  删除后如下图

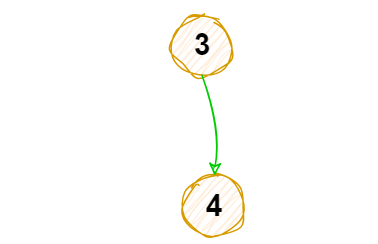
4 输出入度为0的节点，并删除入度为0的节点和此节点对应连线
  入度为0的节点为3，选择输出3，并删3节点和3节点对应连线
  删除后只有节点4，入度为0，所以输出节点4，并删除节点4
本次拓扑排序的顺序为 1-2-3-4

5 接2，可以选择删3
  输出入度为0的节点，并删除入度为0的节点和此节点对应连线
  入度为0的节点为2或3，选择输出3，并删3节点和3节点对应连线
  删除后如下图

6 输出入度为0的节点，并删除入度为0的节点和此节点对应连线
  入度为0的节点为2，选择输出2，并删2节点和2节点对应连线
  删除后只有节点4，入度为0，所以输出节点4，并删除节点4
本次拓扑排序的顺序为 1-3-2-4

所拓扑排序有2种，对应的的顺序是1-2-3-4或1-3-2-4