对称加密系统解析

news2024/10/5 13:56:28

1.概述

2. 对称密码类型

3. 对称加密优缺点

4. 对称加密算法

4.1 DES

4.2 3DES

4.3 AES

4.4 SM1

4.5 SM4

1.概述

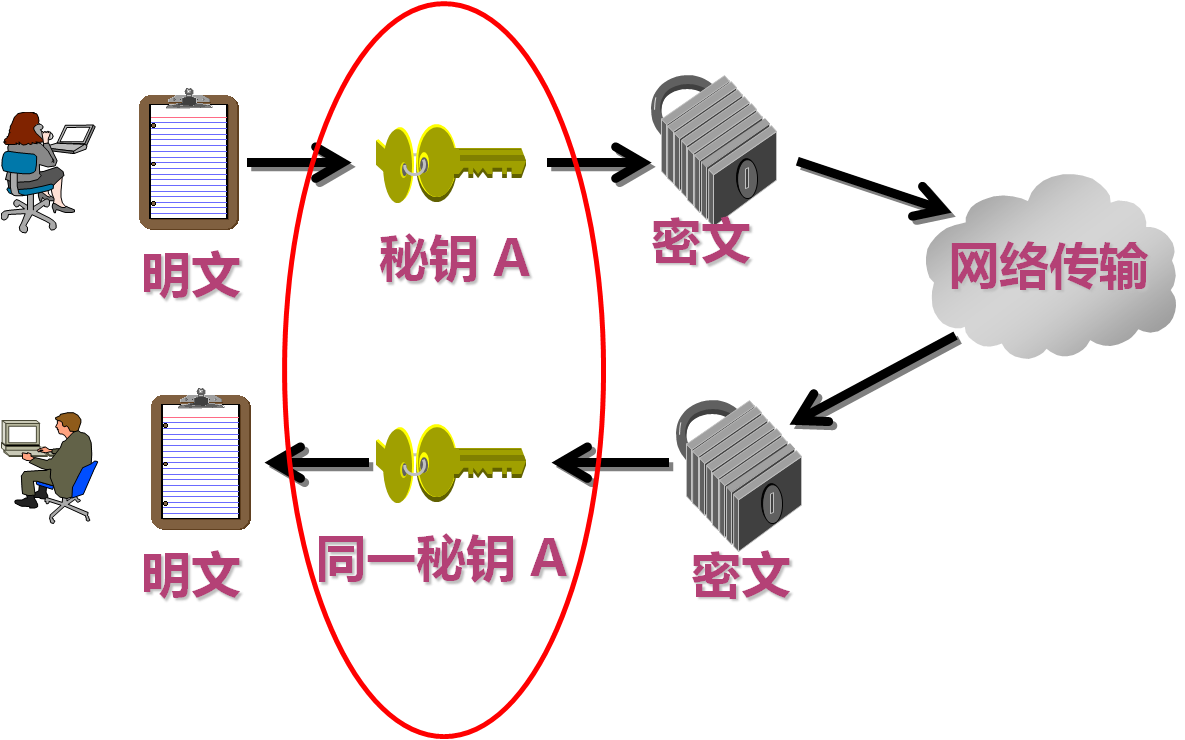
对称加密，是指在加密和解密时使用同一秘钥的方式。秘钥的传送和保存的保护非常重要，务必不要让秘钥被他人窃取。

2. 对称密码类型

序列密码体制
- 序列密码是以一个字符为单位进行加密变换
- 每一字符数据的加密与报文的其他部分无关
- 明文和密文的长度一般不变，多用于通信领域
分组密码体制
- 分组密码将定长的明文块转换成等长的密文
- 电子编码本（ECB）
- 密码分组链接（CBC）或密码反馈（CFB）

3. 对称加密优缺点

优点
- 较非对称加密要快速
- 密钥位数大的话很难被攻破
缺点
- 每一对使用者都需要唯一的密钥，密钥数量较大，管理难度增加
- 提供机密性，但不提供认证和防抵赖功能

4. 对称加密算法

4.1 DES

DES（Data Encryption Standard）是1977年美国联邦信息处理标准（FIPS）中所采用的一种对称密钥（FIPS 46-3）。

然后，随着计算机的进步，DES已经能够被暴力破解，1999年的DES Challenge III中只用了22小时15分钟。由于DES的密文可以在短时间内被破译，因此除了用它来解密以前的密文以外，现在我们不应该再使用DES了。

DES是一种64比特的明文加密成64比特的密文的对称密码算法，它的密钥长度是56比特。（尽管从规格上来说，DES的密钥长度是64比特，但由于每隔7比特会设置一个用于错误检查的比特，因此实质上其秘钥长度是56比特。）

DES是以64比特的明文（比特序列）为一个单位来进行加密的，这个64比特的单位称为分组。一般来说，以分组为单位进行处理的密码算法称为分组密码（block cipher），DES就是分组密码的一种。

DES每次只能加密64比特的数据，如果要加密的明文比较长，就需要对DES加密进行迭代(反复)，而迭代的具体方式就称为模式(mode)。关于模式会在后续的博文中详细介绍。

4.2 3DES

3DES（triple-DES）是为了增加DES的强度，将DES重复3次所得到的一种密码算法，也称为TDES（Triple Data Encryption Algorithm），通常缩写为3DES。

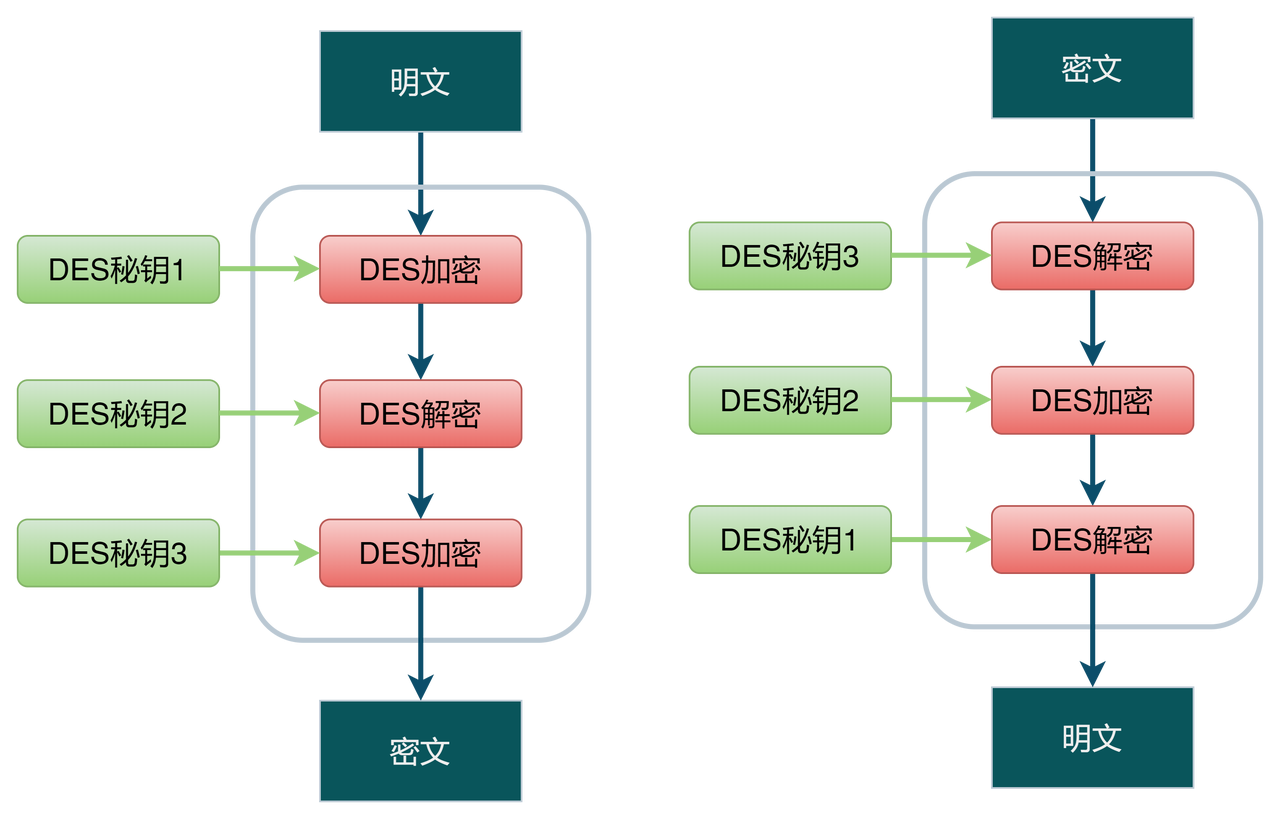
明文经过三次 DES处理才能变成最后的密文，由于DES密钥的长度实质上是56比特，因此三重DES的密钥长度就是56x3=168比特。

三重DES并不是进行三次DES加密(加密→加密一加密)，而是加密一解密一加密的过程。在加密算法中加入解密操作让人感觉很不可思议，实际上这个方法是IBM公司设计出来的，目的是为了让三重DES能够兼容普通的DES。

当三重 DES中所有的密钥都相同时，三重DES也就等同于普通的DES了。这是因为在前两步加密一解密之后，得到的就是最初的明文。因此，以前用 DES加密的密文，就可以通过这种方式用三重 DES来进行解密。也就是说，三重DES对DES具备向下兼容性。

三重 DES 的解密过程和加密正好相反，是以密钥3、密钥2、密钥1的顺序执行解密一加密→解密的操作。

4.3 AES

AES(Advanced Encryption Standard)是取代其前任标准(DES)而成为新标准的一种对称密码算法。全世界的企业和密码学家提交了多个对称密码算法作为AES的候选，最终在2000年从这些候选算法中选出了一种名为Rijndael的对称密码算法，并将其确定为了 AES。

在AES的规格中，分组长度固定为128比特，密钥长度只有128、192和256比特三种。

Rijndael的算法背后有着严谨的数学结构，也就是说从明文到密文的计算过程可以全部用公式来表达，这是以前任何密码算法都不具备的性质。如果Rijndael的公式能够通过数学运算来求解，那也就意味着Riindael能够通过数学方法进行破译。不过，这也只是一种假设而已，实际上到现在为止还没有出现针对Rijndael的有效攻击。

一般来说，我们不应该使用任何自制的密码算法，而是应该使用AES。因为 AES 安全、快速，而且能够在各种平台上工作；在其选定过程中，经过了全世界密码学家所进行的高品质的验证工作，而对于自制的密码算法则很难进行这样的验证。