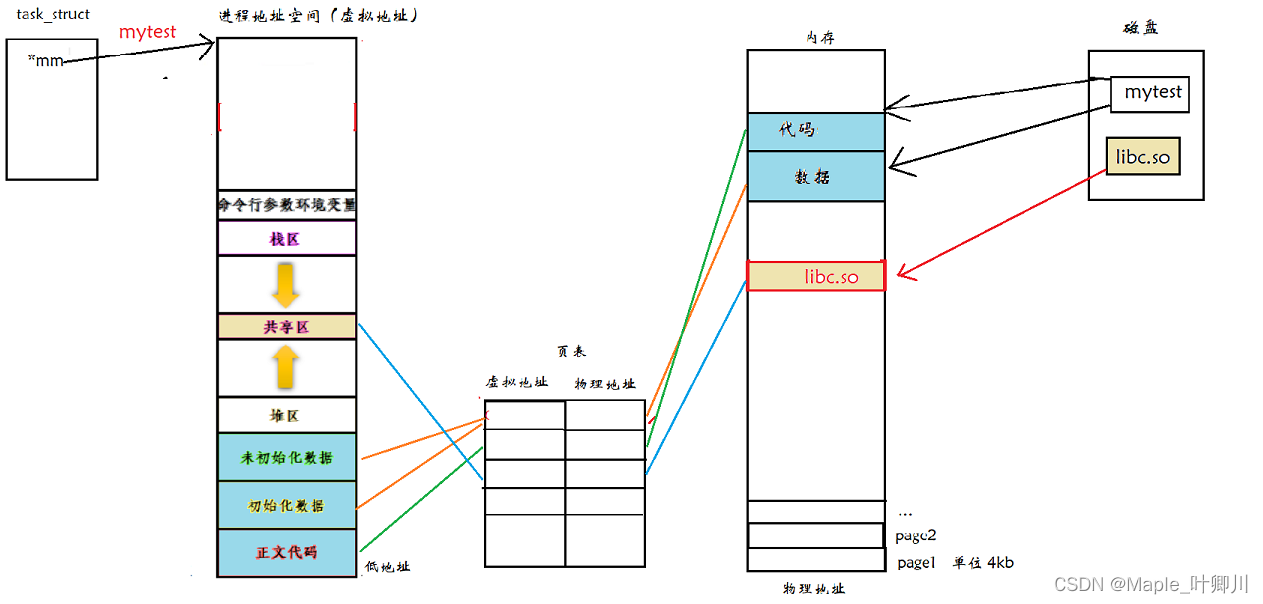
目录
一、概念
二、 插值
2.1方法
2.2MATLAB实现
例题1
编辑例题2
2.3python实现
2.3.1例题一的python解法
2.3.2二维网格节点插值
例题四
三、拟合篇:
3.1MATLAB实现
3.2python实现
一、概念


二、 插值
2.1方法

2.2MATLAB实现
在MATLAB中提供了一些内置函数来实现插值,如interp1(一维插值)、intero2(二维插值)、interp3(三维插值)等等
一维插值使用方法:

例题1

x = 1:12;
y = [5 8 9 15 25 29 31 30 22 25 27 24];
xi = 1:0.01:12;
yi = interp1(x,y,xi,'spline');
plot(x,y,'*',xi,yi,'r')
xlabel('时间'),ylabel('温度')
二维插值使用方法:
 例题2
例题2

%%绘制原图
x = 1:5;
y = 1:3;
wendu = [82 81 80 82 84;
79 63 61 65 81;
84 84 82 85 86];
%mesh(x,y,wendu)
%%开始插值
xi = 1:0.2:5;
yi = 1:0.2:3;
zi = interp2(x,y,wendu,xi',yi,'cubic');
mesh(xi,yi,zi) 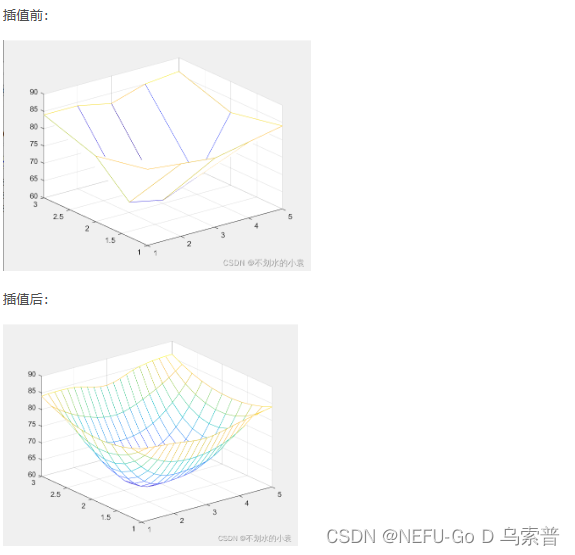
2.3python实现
Scipy.interpolate模块有一维插值函数interp1d,二维插值函数interp2d,多维插值函数interpn,interpnd
interp1d的基本调用格式为
interp1d(x,y,kind=“linear”),返回一个插值函数
kind的取值是字符串,指明插值方法通MATLANB
zero‘ ‘nearest’ :0阶梯插值,相当于0阶B样条曲线
‘slinear’‘linear’ :线性插值,相当于1阶B样条曲线
‘quadratic’‘cubic’:2阶和3阶B样条曲线,更高阶的曲线可以直接使用整数值来指定
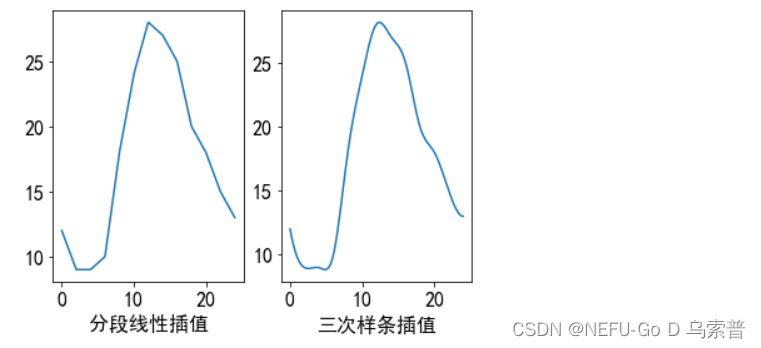
2.3.1例题一的python解法
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d
x=np.arange(0,25,2)
y=np.array([12, 9, 9, 10, 18, 24, 28, 27, 25, 20, 18, 15, 13])
xnew=np.linspace(0, 24, 500) #插值点
f1=interp1d(x, y) #分段线性插值
y1=f1(xnew) #预测
f2=interp1d(x, y,'cubic') #三次样条插值
y2=f2(xnew)
plt.rc('font',size=16); plt.rc('font',family='SimHei') #绘图中文文字输出
plt.subplot(121); plt.plot(xnew, y1); plt.xlabel("分段线性插值")
plt.subplot(122); plt.plot(xnew, y2); plt.xlabel("三次样条插值")
plt.show()
2.3.2二维网格节点插值
例题三

import matplotlib.pyplot as plt
import numpy as np
from numpy.linalg import norm # np.linalg.norm 求范数
from scipy.interpolate import interp2d
z=np.loadtxt("data1_1.txt") #导入数据
x=np.arange(0,1500,100)
y=np.arange(1200,-100,-100) #网格节点数据
f=interp2d(x, y, z, 'cubic') #双三次样条插值
xn=np.linspace(0,1400,141)
yn=np.linspace(0,1200,121) #插值节点
zn=f(xn, yn) #预测
#分块计算面积
m=len(xn); n=len(yn); s=0;
for i in np.arange(m-1):
for j in np.arange(n-1):
p1=np.array([xn[i],yn[j],zn[j,i]])
p2=np.array([xn[i+1],yn[j],zn[j,i+1]])
p3=np.array([xn[i+1],yn[j+1],zn[j+1,i+1]])
p4=np.array([xn[i],yn[j+1],zn[j+1,i]]) #网格四个顶点的 xyz 坐标向量
#分别计算 $\Delta p1p2p3$ 与 $\Delta p1p4p3$ 的面积
p12=norm(p1-p2); p23=norm(p3-p2) #算边长
p13=norm(p3-p1) #公共边(对角线)
p14=norm(p4-p1); p34=norm(p4-p3) #另一个三角形的另两边长
L1=(p12+p23+p13)/2; s1=np.sqrt(L1*(L1-p12)*(L1-p23)*(L1-p13)) # $\Delta p1p2p3$ 的面积
L2=(p13+p14+p34)/2; s2=np.sqrt(L2*(L2-p13)*(L2-p14)*(L2-p34)) # $\Delta p1p4p3$ 的面积
s=s+s1+s2; #求和
print("区域的面积为:", s)
plt.rc('font',size=16); plt.rc('text',usetex=True) # usetex=True
plt.subplot(121); contr=plt.contour(xn,yn,zn); plt.clabel(contr) #画等高线图
plt.xlabel('$x$'); plt.ylabel('$y$',rotation=90)
#画三维表面图
ax=plt.subplot(122,projection='3d');
X,Y=np.meshgrid(xn,yn) #构造网格节点
ax.plot_surface(X, Y, zn,cmap='viridis')
ax.set_xlabel('$x$'); ax.set_ylabel('$y$'); ax.set_zlabel('$z$')
plt.show()
2.3.3二维散乱点插值 (griddata)
import scipy
f=scipy.interpolate.griddata(points, values, xi, method='linear', fill_value=nan, rescale=False)
#参数:
# points: 数据点坐标: (数据量为 n , 维数为 D )
# 具有形状 (n, D) 的浮点数的二维 ndarray,或具有形状 (n, ) 的长度 D 元组的一维 ndarray
# values: 数据值: 浮点数或复数的ndarray,形状 (n, )
# xi: 插入数据的点:
# 具有形状 (m, D) 的二维 ndarray 或长度为 D 元组可广播到相同形状的 ndarray
# method: 插值方法: 可选 {‘linear’, ‘nearest’, ‘cubic’} 之一
# ‘linear’: 分段线性, ‘nearest’: 最近邻点, ‘cubic’: 三次样条
# fill_value: 浮点数,可选,
# 用于填充输入点凸包之外的请求点的值。如果未提供,则默认值为 NaN , 此选项对‘nearest’ 方法无效
# rescale: 布尔型,可选
# 在执行插值之前将点重新缩放到单位立方体 (如果某些输入维度具有不可比较的单位并且相差许多数量级时可以使用)
#返回: ndarray 插值数组
例题四

import matplotlib.pyplot as plt
import numpy as np
from scipy.interpolate import griddata
x=np.array([129,140,103.5,88,185.5,195,105,157.5,107.5,77,81,162,162,117.5])
y=np.array([7.5,141.5,23,147,22.5,137.5,85.5,-6.5,-81,3,56.5,-66.5,84,-33.5])
z=-np.array([4,8,6,8,6,8,8,9,9,8,8,9,4,9])
xy=np.vstack([x,y]).T
xn=np.linspace(x.min(), x.max(), 100)
yn=np.linspace(y.min(), y.max(), 100) #生成插值点
xng, yng = np.meshgrid(xn,yn) #构造网格节点
zn=griddata(xy, z, (xng, yng), method='nearest') #最近邻点插值
plt.rc('font',size=16); plt.rc('text',usetex=True)
ax=plt.subplot(121,projection='3d')
ax.plot_surface(xng, yng, zn,cmap='viridis') #画地形图
ax.set_xlabel('$x$'); ax.set_ylabel('$y$'); ax.set_zlabel('$z$')
plt.subplot(122); c=plt.contour(xn,yn,zn,8); plt.clabel(c) #画等高线图
plt.show()
三、拟合篇:
3.1MATLAB实现
对于已给一批实测数据,由于实测方法、实验环境等一些外界因素的影响,不可避免地会产生随机干扰和误差。我们自然希望根据数据分布的总趋势去剔除观察数据中的偶然误差,这就是所谓的数据修匀(或称数据平滑)问题。
同样,在MATLAB中也存在着拟合函数的内置函数,如对多项式:进行拟和
可利用已有程序:a = ployfit(x,y,m) 注意:m为拟合多项式的次数
多项式在x出的值y可以用以下命令计算:y = ployval(a,x)
x = 0:0.1:1;
y = [-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2];
A = polyfit(x,y,2) %A为拟合出来的函数
z = polyval(A,x); %求多项式在x处的值z
plot(x,y,'k+',x,z,'r')拟合结果

3.2python实现