谢谢观看！希望以下内容帮助到了你，对你起到作用的话，可以一键三连加关注！你们的支持是我更新地动力。
因作者水平有限，有错误还请指出，多多包涵，谢谢！

---

一、联合体类型的声明

  

//联合体的关键字：union
//结构体的关键字：struct
//枚举的关键：enum

struct s
{
	char c;//0
	//1~3 浪费了
	int i;//4~7
};

union un//联合体的声明
{
	char c;
	int i;
};

int main()
{
	printf("%zd\n", sizeof(struct s));//8
	printf("%zd\n", sizeof(union un));//4

	return 0;
}

  

---

二、联合体的特点

  
  联合体的特点：联合的成员是共用同一块内存空间的，这样一个联合变量的大小，至少是最大成员的大小（因为联合至少得有能力保存最大的那个成员），但不一定等于最大成员的大小。
  

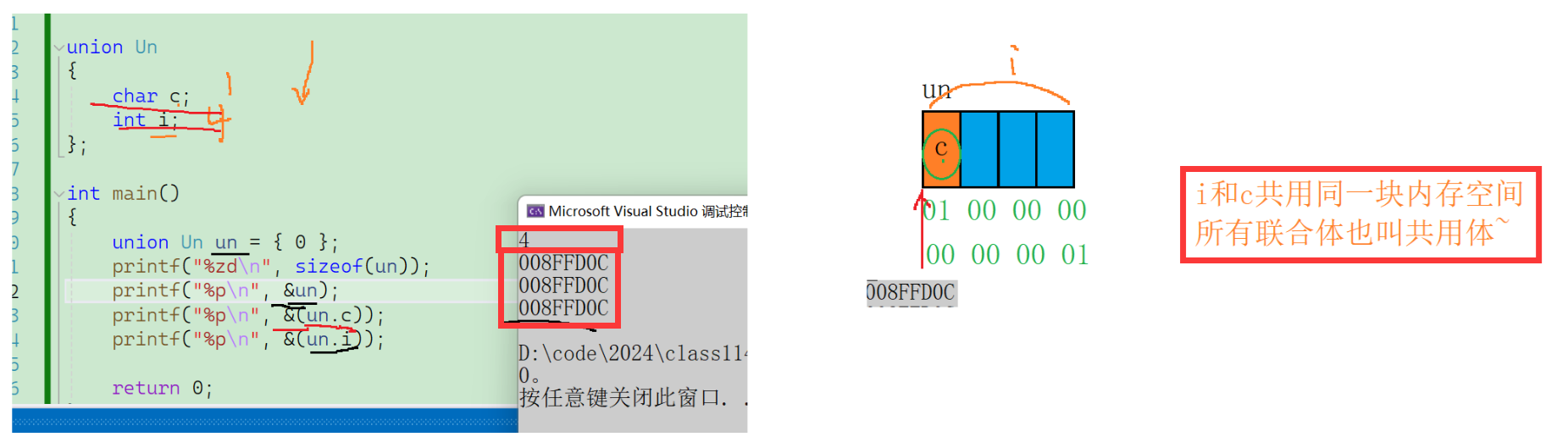
  虽然我们知道了它们是同一个起始地址，但是该如何具体的看到内存的变化呢？其实我们可以通过调试窗口观察

//代码2
#include <stdio.h>
//联合类型的声明
union Un
{
 char c;
 int i;
};
int main()
{
 //联合变量的定义
 union Un un = {0};
 un.i = 0x11223344;
 un.c = 0x55;
 printf("%x\n", un.i);
 return 0;
}

  变化之前：
  

  变化之后：
  

  
  通过上面的代码比较可以看出：联合的成员是共用同一块内存空间的
  

---

三、联合体大小的计算

  
联合体大小计算规则：

• 联合的大小至少是最大成员的大小。
• 当最大成员大小不是最大对齐数的整数倍的时候，就要对齐到最大对齐数的整数倍。

union Un
{
	short arr[7];//14    2 8 2
	//将数组拆开相当于有7个short的数据
	int i;//4            4 8 4
	//所以实际最大对齐数是4，那么联合体的整体大小是实际最大对齐数的整数倍
	//14不是，16是，那么浪费了2个字节
};

int main()
{
	printf("%d\n", sizeof(union Un));//结果是16

	return 0;
}

四、联合的一个练习

  写⼀个程序，判断当前机器是大端？还是小端？

int check_sys()
{
    union
    {
        int i;
        char c;
    }un;
    un.i = 1;
    return un.c;//返回1是⼩端，返回0是⼤端
}

int main()
{
    check_sys();
    return 0;
}