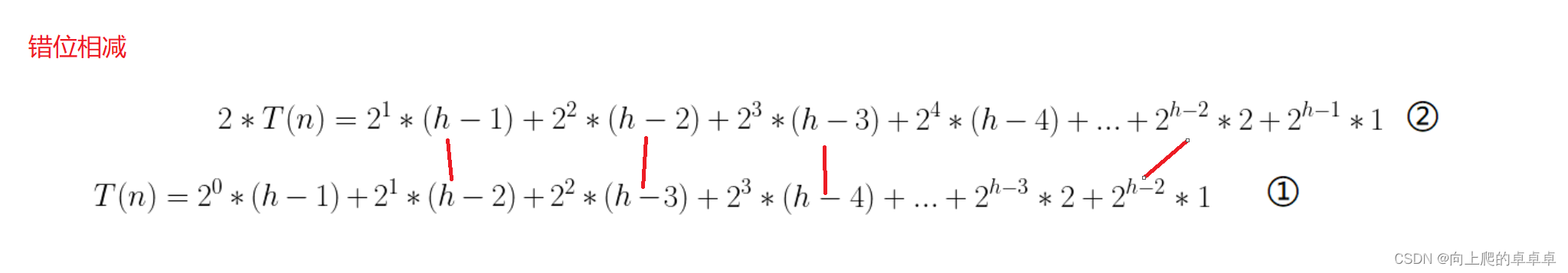前言
在上一篇文章主要讲解了二叉树的基本概念和堆的概念以及接口的实现(点此处跳转)
我们简回顾下堆的基本概念:
1.堆分为大堆和小堆
- 大堆:父亲结点比左右孩子都大,根结点是最大的
- 小堆:父亲结点比左右孩子都小,根结点是最小的
2.堆是一颗完全二叉树,所以堆适合使用数组来创建
3.堆仅仅约束了父子之间的大小关系,但并没有规定左右孩子之间的大小关系
一.建堆(大堆)
这里的建堆不是说创建堆这个数据结构,而是将一个无序的数组调整成堆的顺序,建堆有两种方法;向上调整建堆与向下调整建堆。
1.向上调整建堆
我们把数组的第一个元素看成一个堆,把第二个元素想象成要插入堆的数据,然后之后向上调整;然后再进行插入这样一直下去,直到调整完数组的最后一个元素,这样一个堆就建好了。
//向上调整算法
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[parent] < a[child])
{
Swap(&a[parent], &a[child]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
//向上调整建堆
void CreateHeap(int* a, int n)
{
for (int i = 1; i < n; i++)
{
AdjustUp(a, i);
}
}
int main()
{
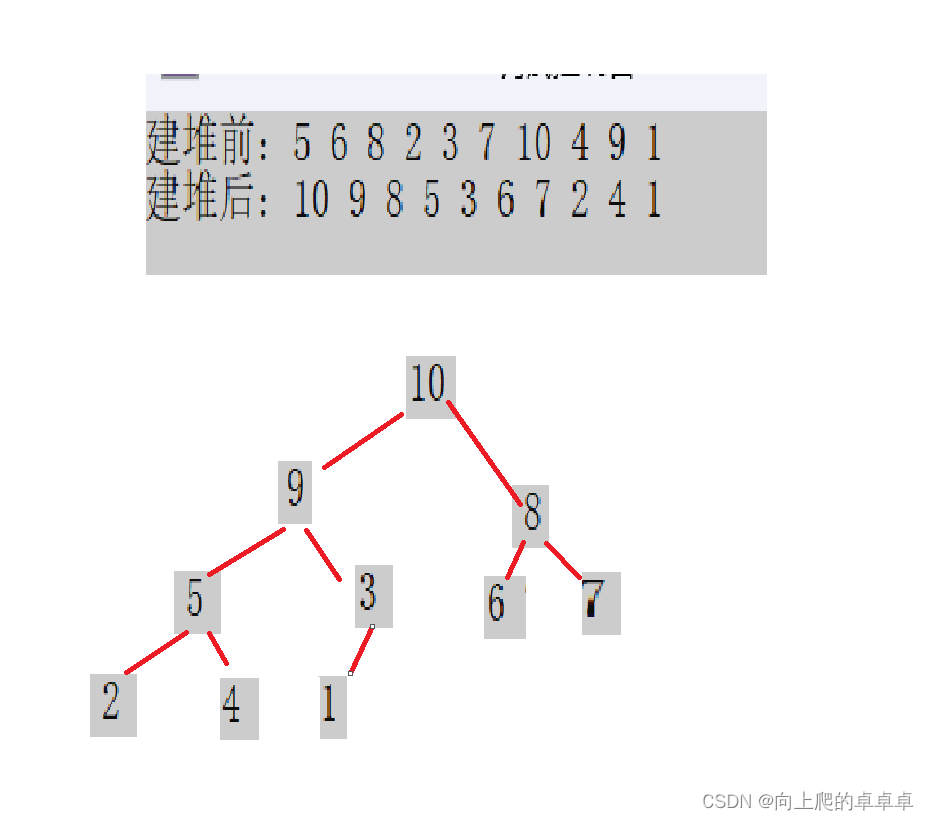
int a[] = { 5,6,8,2,3,7,10,4,9,1 };
printf("建堆前:");
PrintArray(a, sizeof(a) / sizeof(int));
CreateHeap(a, sizeof(a) / sizeof(int));
printf("建堆后:");
PrintArray(a, sizeof(a) / sizeof(int));
return 0;
}
2.向下调整建堆
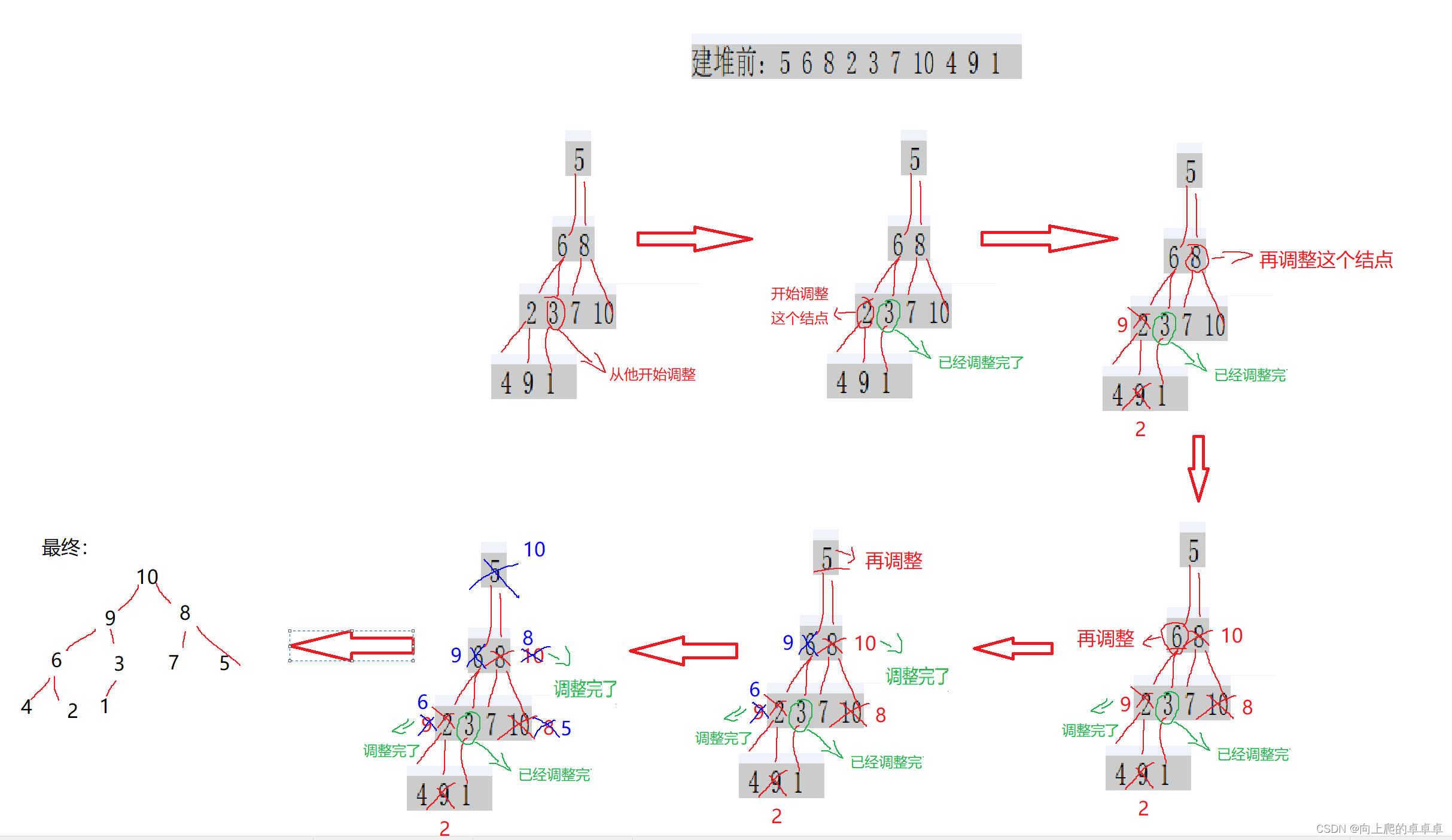
向下调整有一个限制条件,左右子树必须是堆,这也就代表了向下调整不能像向上调整一样从根结点开始调整。
既让要满足左右子树都必须是堆,那我们就从最后一个父结点开始调整,因为这样左右子树都只剩下一个结点,我们可以直接将这一个结点看成堆。
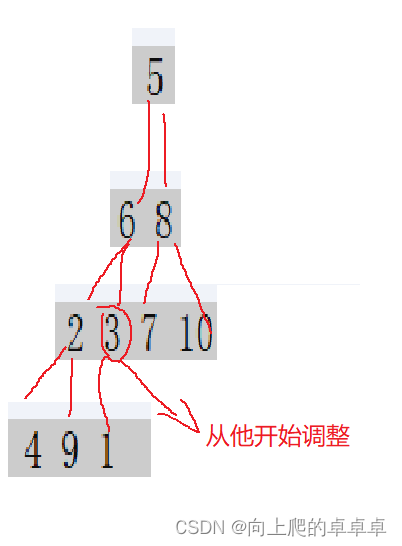
每调整一次,就找调整完的后一个父节点,直到调整完根结点,如图:
//向下调整算法
void AdjustDown(HPDataType* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
if (child+1 < n && a[child] < a[child + 1])
{
child++;
}
if (a[parent] < a[child])
{
Swap(&a[parent], &a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
//向下调整创建堆
void CreateHeap(int* a, int n)
{
for (int i = (n-1-1)/2; i >= 0; i--)
{
AdjustDown(a, n,i);
}
}
int main()
{
int a[] = { 5,6,8,2,3,7,10,4,9,1 };
printf("建堆前:");
PrintArray(a, sizeof(a) / sizeof(int));
CreateHeap(a, sizeof(a) / sizeof(int));
printf("建堆后:");
PrintArray(a, sizeof(a) / sizeof(int));
return 0;
}

3.向上调整与向下调整的对比
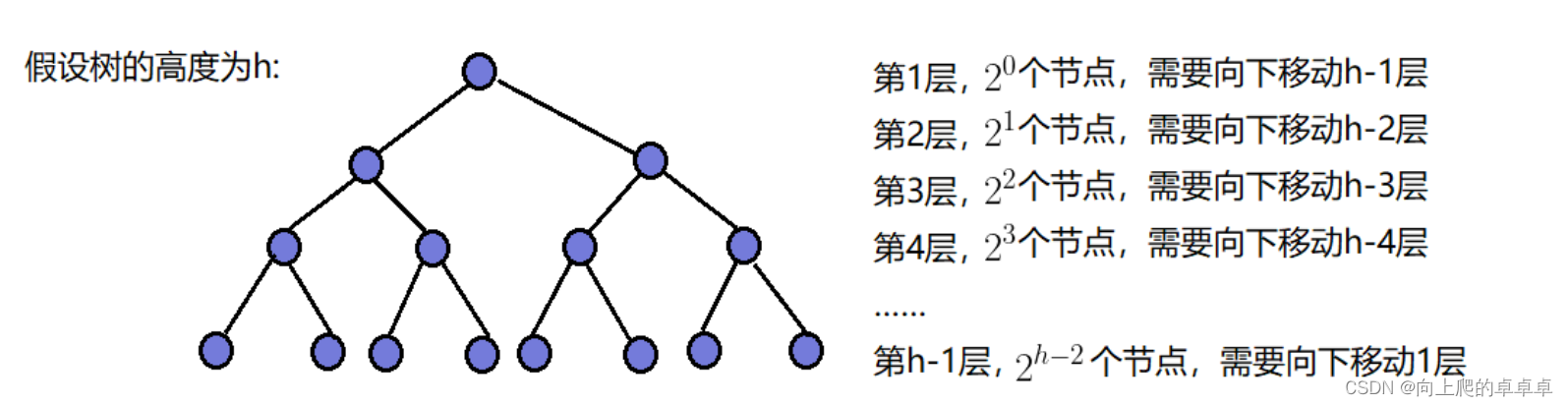
向下调整建堆的时间复杂度比向上调整的时间复杂度低
假设这个堆有h层,我们向下调整的时候是从第h-1层开始调整,这时的h-1层有
2
h
−
2
2^{h-2}
2h−2个结点,每个结点要调整一次,越往上走调整的越少,直到第一层,也就是根结点的时候,根结点要向下调整h-1次
这时候调整的总步数为:
T ( n ) = 2 0 ∗ ( h − 1 ) + 2 1 ∗ ( h − 2 ) + 2 2 ∗ ( h − 3 ) + . . . . . . + 2 h − 3 ∗ 2 + 2 h − 2 ∗ 1 T(n) = 2^0*(h-1) + 2^1*(h-2) + 2^2*(h-3) + ...... +2^{h-3}*2 + 2^{h-2}*1 T(n)=20∗(h−1)+21∗(h−2)+22∗(h−3)+......+2h−3∗2+2h−2∗1
我们对他进行×2操作
2 T ( n ) = 2 1 ∗ ( h − 1 ) + 2 2 ∗ ( h − 2 ) + 2 3 ∗ ( h − 3 ) + . . . . . . + 2 h − 2 ∗ 2 + 2 h − 1 ∗ 1 2T(n) = 2^1*(h-1) + 2^2*(h-2) + 2^3*(h-3) + ...... +2^{h-2}*2 + 2^{h-1}*1 2T(n)=21∗(h−1)+22∗(h−2)+23∗(h−3)+......+2h−2∗2+2h−1∗1
这就形成了错位,这时我们继续错位相减
2 T ( n ) − T ( n ) = 2 1 ∗ ( h − 1 ) + 2 2 ∗ ( h − 2 ) + 2 3 ∗ ( h − 3 ) + . . . . . . + 2 h − 2 ∗ 2 + 2 h − 1 ∗ 1 − [ 2 0 ∗ ( h − 1 ) + 2 1 ∗ ( h − 2 ) + 2 2 ∗ ( h − 3 ) + . . . . . . + 2 h − 3 ∗ 2 + 2 h − 2 ∗ 1 ] 2T(n)-T(n) = 2^1*(h-1) + 2^2*(h-2) + 2^3*(h-3) + ...... +2^{h-2}*2 + 2^{h-1}*1-[2^0*(h-1) + 2^1*(h-2) + 2^2*(h-3) + ...... +2^{h-3}*2 + 2^{h-2}*1] 2T(n)−T(n)=21∗(h−1)+22∗(h−2)+23∗(h−3)+......+2h−2∗2+2h−1∗1−[20∗(h−1)+21∗(h−2)+22∗(h−3)+......+2h−3∗2+2h−2∗1]
T ( n ) = 2 1 + 2 2 + 2 3 + . . . . . . + 2 h − 3 + 2 h − 2 + 2 h − 1 − ( h − 1 ) T(n) = 2^1+ 2^2+2^3+......+2^{h-3}+2^{h-2}+2^{h-1}-(h-1) T(n)=21+22+23+......+2h−3+2h−2+2h−1−(h−1)
T ( n ) = 1 − h + 2 1 + 2 2 + 2 3 + . . . . . . + 2 h − 3 + 2 h − 2 + 2 h − 1 T(n) =1-h+2^1+ 2^2+2^3+......+2^{h-3}+2^{h-2}+2^{h-1} T(n)=1−h+21+22+23+......+2h−3+2h−2+2h−1
T ( n ) = 2 0 + 2 1 + 2 2 + 2 3 + . . . . . . + 2 h − 3 + 2 h − 2 + 2 h − 1 − h T(n)=2^0+2^1+ 2^2+2^3+......+2^{h-3}+2^{h-2}+2^{h-1}-h T(n)=20+21+22+23+......+2h−3+2h−2+2h−1−h
T ( n ) = 2 h − 1 − h T(n)=2^h-1-h T(n)=2h−1−h
之前在二叉树的性质里讲过,一颗满二叉的的结点数量为: 2 h − 1 2^h-1 2h−1,其高度为: h = l o g 2 ( n + 1 ) h=log_2(n+1) h=log2(n+1)
将这两个结果套到 T ( n ) T(n) T(n)中
T ( n ) = n − l o g 2 ( n + 1 ) ≈ n T(n) = n-log_2(n+1) \approx n T(n)=n−log2(n+1)≈n(时间复杂度取影响最大的因素)
向下调整建堆,是大的项×小的项,其时间复杂度为O(n)
向上调整建堆我就不细讲了,就拿一组数据就能发现为什么向上调整会比向下调整慢了,
向上调整建堆是从一个左孩子开始调整(第二层),这时是需要向上调整一次,第三层需要向上调整两次;这样一直往下直到最后一层,这时调整次数就来到了恐怖的
2
h
−
1
∗
(
h
−
1
)
2^h-1*(h-1)
2h−1∗(h−1)次,也就是是最后一层的每个结点都要调整
h
−
1
h-1
h−1次(最后一层的数据就占了堆的一半)
这时总步数为:
T
(
n
)
=
2
1
∗
2
+
2
2
∗
2
+
2
3
∗
3
+
.
.
.
.
.
.
+
2
h
−
2
∗
(
h
−
2
)
+
2
h
−
1
∗
(
h
−
1
)
T(n) = 2^1*2+2^2*2+2^3*3+......+2^{h-2}*(h-2)+2^{h-1}*(h-1)
T(n)=21∗2+22∗2+23∗3+......+2h−2∗(h−2)+2h−1∗(h−1)
这时非常恐怖的数据量
直接说结论:向上调整建堆的时间复杂度为O(N*logN)
总结:向下调整建堆的时间复杂度为O(N),向上调整建堆的时间复杂度为O(N*logN),所以为了效率,更推荐使用向下调整建堆
二.堆排序
既然堆已经建好了,那我们就开始排序把。
排序的过程:
- 将堆顶的数据与堆底交换,将原来堆顶的数据不看做堆
- 重新进行向下调整
排序每次调换的都是堆顶的数据,所以当我是大堆的时候,每次被交换的数据都是在当前堆中最大的数,小堆同理。
所以当我们要排升序的时候建大堆,要排降序的时候建小堆。
//向下调整算法
void AdjustDown(HPDataType* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
if (child+1 < n && a[child] < a[child + 1])
{
child++;
}
if (a[parent] < a[child])
{
Swap(&a[parent], &a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//向下调整创建堆
void CreateHeap(int* a, int n)
{
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
}
//堆排序
void HeapSort(int* a, int n)
{
CreateHeap(a, n);
int end = n - 1;//堆底
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}

完整代码
//向下调整算法
void AdjustDown(HPDataType* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
if (child+1 < n && a[child] < a[child + 1])
{
child++;
}
if (a[parent] < a[child])
{
Swap(&a[parent], &a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//向下调整创建堆
void CreateHeap(int* a, int n)
{
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
}
//堆排序
void HeapSort(int* a, int n)
{
CreateHeap(a, n);
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
int main()
{
int a[] = { 5,6,8,2,3,7,10,4,9,1 };
printf("排序前:");
PrintArray(a, sizeof(a) / sizeof(int));
//CreateHeap(a, sizeof(a) / sizeof(int));
HeapSort(a,sizeof(a) / sizeof(int));
printf("排序后:");
PrintArray(a, sizeof(a) / sizeof(int));
return 0;
}
结语
最后感谢您能阅读完此片文章,如果有任何建议或纠正欢迎在评论区留言,也可以前往我的主页看更多好文哦(点击此处跳转到主页)。
如果您认为这篇文章对您有所收获,点一个小小的赞就是我创作的巨大动力,谢谢!!!