SLAM小题目

news2024/11/26 8:47:36

1、最小二乘题目：

        假设有三个WIFI热点，位置分别在(x1,y1), (x2,y2), (x3,y3), 移动端测量到每一个热点的距离L1,L2和L3，要求解移动端的位置. 

#include <iostream>
#include <vector>
#include <cmath> 

class Point {
public:
    double x, y;
};

Point test(const std::vector<Point>& location, const std::vector<double>& distances) {

    double x1 = location[0].x, y1 = location[0].y, L1 = distances[0];
    double x2 = location[1].x, y2 = location[1].y, L2 = distances[1];
    double x3 = location[2].x, y3 = location[2].y, L3 = distances[2];

    double a1 = 2 * (x2 - x1);
    double b1 = 2 * (y2 - y1);
    double c1 = L1 * L1 - L2 * L2 + x2 * x2 - x1 * x1 + y2 * y2 - y1 * y1;

    double a2 = 2 * (x3 - x1);
    double b2 = 2 * (y3 - y1);
    double c2 = L1 * L1 - L3 * L3 + x3 * x3 - x1 * x1 + y3 * y3 - y1 * y1;

    Point result;
    result.x = (c1 * b2 - c2 * b1) / (a1 * b2 - a2 * b1);
    result.y = (a1 * c2 - a2 * c1) / (a1 * b2 - a2 * b1);

    return result;
}

int main() {
    std::vector<Point> location = {{0, 0}, {1, 0}, {0, 1}};
    double sqrt_2 = std::sqrt(2.0);
    std::vector<double> distances = {sqrt_2, 1.0, 1.0};
    Point result = test(location, distances);
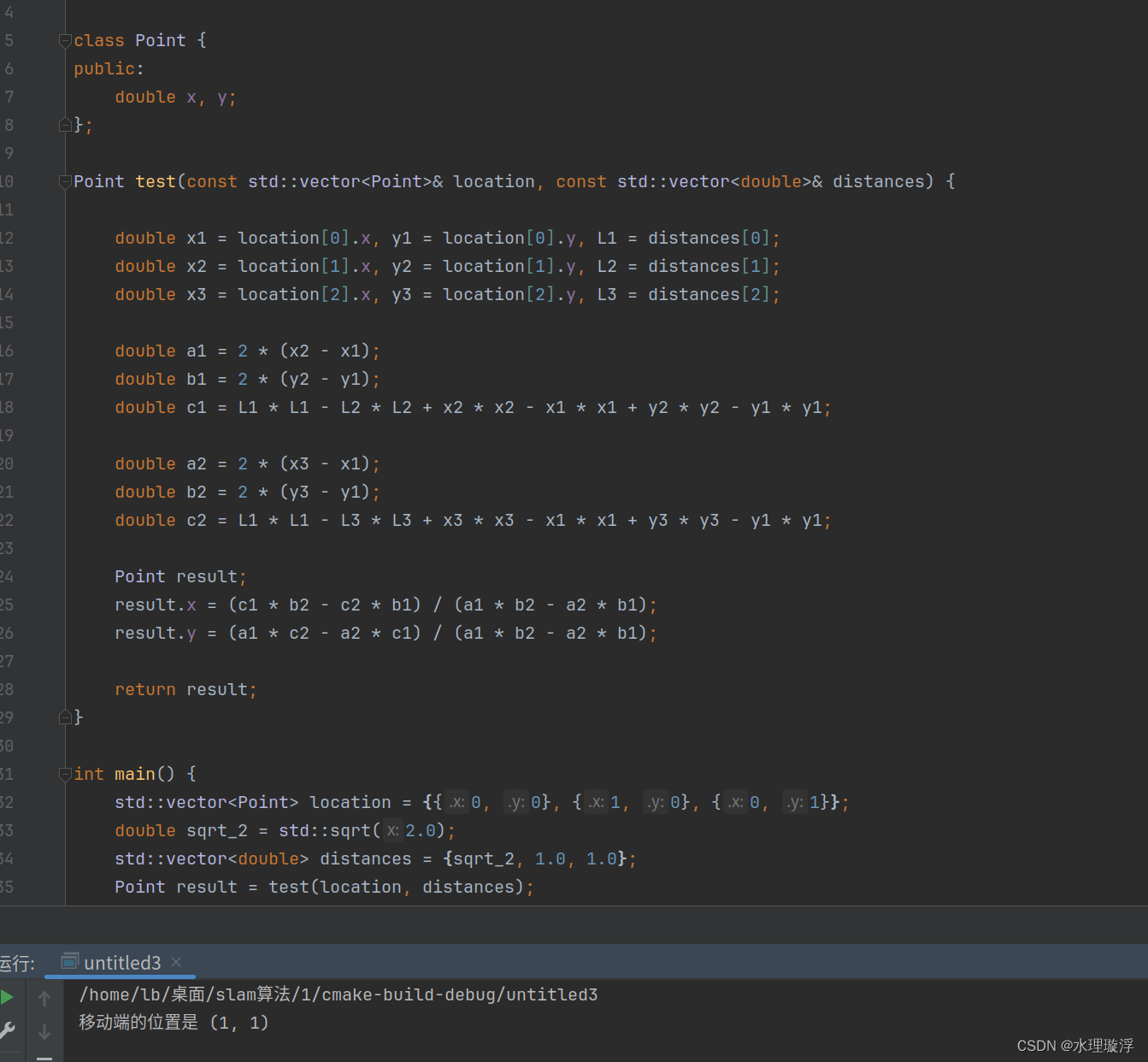
    std::cout << "移动端的位置是 (" << result.x << ", " << result.y << ")" << std::endl;
    return 0;
}

2、图像题目

已知相机内参：520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1。求解两帧图像之间的运动。

    a.部署OpenCV等环境，使用熟悉的特征点匹配后计算。

    b.运动求解过程需要亲自编写程序，不允许调用第三方库。

CMakeLists.txt

cmake_minimum_required(VERSION 2.8)
project(vo1)

set(CMAKE_BUILD_TYPE "Release")
add_definitions("-DENABLE_SSE")
set(CMAKE_CXX_FLAGS "-std=c++14 -O2 ${SSE_FLAGS} -msse4")
#list(APPEND CMAKE_MODULE_PATH ${PROJECT_SOURCE_DIR}/cmake)

find_package(OpenCV 3.4.15 REQUIRED)
#find_package(G2O REQUIRED)
#find_package(Sophus REQUIRED)

include_directories(
        ${OpenCV_INCLUDE_DIRS}
       # ${G2O_INCLUDE_DIRS}
       # ${Sophus_INCLUDE_DIRS}
        "/usr/include/eigen3/"
)

# add_executable( pose_estimation_2d2d pose_estimation_2d2d.cpp extra.cpp ) # use this if in OpenCV2 
add_executable(pose_estimation_2d2d pose_estimation_2d2d.cpp)
target_link_libraries(pose_estimation_2d2d ${OpenCV_LIBS})

主函数

#include <iostream>
#include <opencv2/core/core.hpp>
#include <opencv2/features2d/features2d.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/calib3d/calib3d.hpp>
#include <vector>
#include <random>
#include <ctime>
#include <Eigen/Dense>
using namespace std;
using namespace cv;
using namespace Eigen;

void find_feature_matches(
  const Mat &img_1, const Mat &img_2,
  std::vector<KeyPoint> &keypoints_1,
  std::vector<KeyPoint> &keypoints_2,
  std::vector<DMatch> &matches);

void pose_estimation_2d2d(
  std::vector<KeyPoint> keypoints_1,
  std::vector<KeyPoint> keypoints_2,
  std::vector<DMatch> matches,
  Mat &R, Mat &t);

const int MAX_ITER = 100000;  // 最大迭代次数
const float THRESHOLD = 0.001;  // 内点距离阈值


float calculateError(const Matrix3f& F, const Point2f& pt1, const Point2f& pt2) {
    Vector3f p1(pt1.x, pt1.y, 1.0);
    Vector3f p2(pt2.x, pt2.y, 1.0);
    Vector3f line = F * p1;
    return fabs(p2.dot(line)) / sqrt(line[0] * line[0] + line[1] * line[1]);
}

Matrix3f ransacFundamentalMat(const vector<Point2f>& points1, const vector<Point2f>& points2) {
    int bestInliersCount = 0;
    Matrix3f bestF;
    std::default_random_engine rng(time(0));
    std::uniform_int_distribution<int> uniDist(0, points1.size() - 1);

    for (int iter = 0; iter < MAX_ITER; ++iter) {
        vector<Point2f> samplePoints1, samplePoints2;
        for (int i = 0; i < 8; ++i) {
            int idx = uniDist(rng);
            samplePoints1.push_back(points1[idx]);
            samplePoints2.push_back(points2[idx]);
        }

        int N = samplePoints1.size();
        MatrixXf A(N, 9);

        for (int i = 0; i < N; ++i) {
            float x1 = samplePoints1[i].x;
            float y1 = samplePoints1[i].y;
            float x2 = samplePoints2[i].x;
            float y2 = samplePoints2[i].y;
            A.row(i) << x2 * x1, x2 * y1, x2, y2 * x1, y2 * y1, y2, x1, y1, 1;
        }

        JacobiSVD<MatrixXf> svd(A, ComputeFullV);
        VectorXf f = svd.matrixV().col(8);

        Matrix3f F;
        F << f(0), f(1), f(2),
                f(3), f(4), f(5),
                f(6), f(7), f(8);

        JacobiSVD<Matrix3f> svdF(F, ComputeFullU | ComputeFullV);
        Vector3f singularValues = svdF.singularValues();
        singularValues[2] = 0;
        F = svdF.matrixU() * singularValues.asDiagonal() * svdF.matrixV().transpose();

        int inliersCount = 0;
        for (int i = 0; i < points1.size(); ++i) {
            if (calculateError(F, points1[i], points2[i]) < THRESHOLD) {
                ++inliersCount;
            }
        }

        if (inliersCount > bestInliersCount) {
            bestInliersCount = inliersCount;
            cout<<bestInliersCount<<endl;
            bestF = F;
        }
    }

    return bestF;
}
void recoverPose_my(const Matrix3f& essential_matrix, const vector<Point2f>& points1, const vector<Point2f>& points2, Matrix3f& R, Vector3f& t, double focal_length, const Point2d& principal_point) {
    // SVD分解本质矩阵
    JacobiSVD<Matrix3f> svd(essential_matrix, ComputeFullU | ComputeFullV);
    Matrix3f U = svd.matrixU();
    Matrix3f Vt = svd.matrixV().transpose();

    // 构造W矩阵和Z矩阵
    Matrix3f W;
    W << 0, -1, 0,
            1, 0, 0,
            0, 0, 1;

    Matrix3f Z;
    Z << 0, 1, 0,
            -1, 0, 0,
            0, 0, 0;

    // 可能的两种旋转矩阵
    Matrix3f R1 = U * W * Vt;
    if (R1.determinant() < 0) {
        R1 = -R1;
    }
    Matrix3f R2 = U * W.transpose() * Vt;
    if (R2.determinant() < 0) {
        R2 = -R2;
    }

    // 平移向量
    Vector3f t1 = U.col(2);
    Vector3f t2 = -U.col(2);

    // 对两个可能的解进行验证，选择最合适的那个
    int valid_count1 = 0;
    int valid_count2 = 0;

    for (int i = 0; i < points1.size(); ++i) {
        Vector3f p1(points1[i].x, points1[i].y, 1.0);
        Vector3f p2(points2[i].x, points2[i].y, 1.0);

        p1[0] = (p1[0] - principal_point.x) / focal_length;
        p1[1] = (p1[1] - principal_point.y) / focal_length;
        p2[0] = (p2[0] - principal_point.x) / focal_length;
        p2[1] = (p2[1] - principal_point.y) / focal_length;

        // 计算重投影误差来判断是否在相机前方
        Vector3f p1_proj = R1 * p2 + t1;
        if (p1_proj[2] > 0) {
            ++valid_count1;
        }

        p1_proj = R2 * p2 + t2;
        if (p1_proj[2] > 0) {
            ++valid_count2;
        }
    }

    if (valid_count1 > valid_count2) {
        R = R1;
        t = t1;
    } else {
        R = R2;
        t = t2;
    }
}

int main() {

  //-- 读取图像
  Mat img_1 = imread("../1.png", CV_LOAD_IMAGE_COLOR);
  Mat img_2 = imread("../2.png", CV_LOAD_IMAGE_COLOR);
    if (img_1.empty() || img_2.empty()) {
        cerr << "无法加载图片" << endl;
        return -1;
    }

  vector<KeyPoint> keypoints_1, keypoints_2;
  vector<DMatch> matches;
  find_feature_matches(img_1, img_2, keypoints_1, keypoints_2, matches);
  cout << "一共找到了" << matches.size() << "组匹配点" << endl;

  //-- 估计两张图像间运动
  Mat R, t;
  pose_estimation_2d2d(keypoints_1, keypoints_2, matches, R, t);

  return 0;
}

void find_feature_matches(const Mat &img_1, const Mat &img_2,
                          std::vector<KeyPoint> &keypoints_1,
                          std::vector<KeyPoint> &keypoints_2,
                          std::vector<DMatch> &matches) {
  //-- 初始化
  Mat descriptors_1, descriptors_2;
  // used in OpenCV3
  Ptr<FeatureDetector> detector = ORB::create();
  Ptr<DescriptorExtractor> descriptor = ORB::create();
  Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create("BruteForce-Hamming");
  //-- 第一步:检测 Oriented FAST 角点位置
  detector->detect(img_1, keypoints_1);
  detector->detect(img_2, keypoints_2);

  //-- 第二步:根据角点位置计算 BRIEF 描述子
  descriptor->compute(img_1, keypoints_1, descriptors_1);
  descriptor->compute(img_2, keypoints_2, descriptors_2);

  //-- 第三步:对两幅图像中的BRIEF描述子进行匹配，使用 Hamming 距离
  vector<DMatch> match;
  //BFMatcher matcher ( NORM_HAMMING );
  matcher->match(descriptors_1, descriptors_2, match);

  //-- 第四步:匹配点对筛选
  double min_dist = 10000, max_dist = 0;

  //找出所有匹配之间的最小距离和最大距离, 即是最相似的和最不相似的两组点之间的距离
  for (int i = 0; i < descriptors_1.rows; i++) {
    double dist = match[i].distance;
    if (dist < min_dist) min_dist = dist;
    if (dist > max_dist) max_dist = dist;
  }

  printf("-- Max dist : %f \n", max_dist);
  printf("-- Min dist : %f \n", min_dist);

  //当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限.
  for (int i = 0; i < descriptors_1.rows; i++) {
    if (match[i].distance <= max(2 * min_dist, 30.0)) {
      matches.push_back(match[i]);
    }
  }
    Mat img_matches;
    drawMatches(img_1, keypoints_1, img_2, keypoints_2, matches, img_matches);

    // 显示匹配结果
    imshow("按任意键继续！", img_matches);
    waitKey();
}


void pose_estimation_2d2d(std::vector<KeyPoint> keypoints_1,
                          std::vector<KeyPoint> keypoints_2,
                          std::vector<DMatch> matches,
                          Mat &R, Mat &t) {
  // 相机内参,TUM Freiburg2
  Mat K = (Mat_<double>(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);

  //-- 把匹配点转换为vector<Point2f>的形式
  vector<Point2f> points1;
  vector<Point2f> points2;

  for (int i = 0; i < (int) matches.size(); i++) {
    points1.push_back(keypoints_1[matches[i].queryIdx].pt);
    points2.push_back(keypoints_2[matches[i].trainIdx].pt);
  }

  //-- 计算本质矩阵
  Point2d principal_point(325.1, 249.7);  //相机光心
  double focal_length = 521;      //相机焦距
  Mat essential_matrix;
  essential_matrix = findEssentialMat(points1, points2, focal_length, principal_point);

  // 内参矩阵K
  Matrix3f k;
  k << focal_length, 0, principal_point.x,
   0, focal_length, principal_point.y,
   0, 0, 1;

  // 计算本质矩阵
  Matrix3f fundamental_matrix_ransac;
  fundamental_matrix_ransac =  ransacFundamentalMat(points1, points2);
  Matrix3f E = k.transpose() * fundamental_matrix_ransac * k;
  JacobiSVD<Matrix3f> svdE(E, ComputeFullU | ComputeFullV);
  Vector3f singularValues = svdE.singularValues();
  singularValues[2] = 0;
  E = svdE.matrixU() * singularValues.asDiagonal() * svdE.matrixV().transpose();
  //-- 从本质矩阵中恢复旋转和平移信息.
  recoverPose(essential_matrix, points1, points2, R, t, focal_length, principal_point);
  Matrix3f R1;
  Vector3f t1;
  recoverPose_my(  E , points1, points2, R1, t1, focal_length, principal_point);
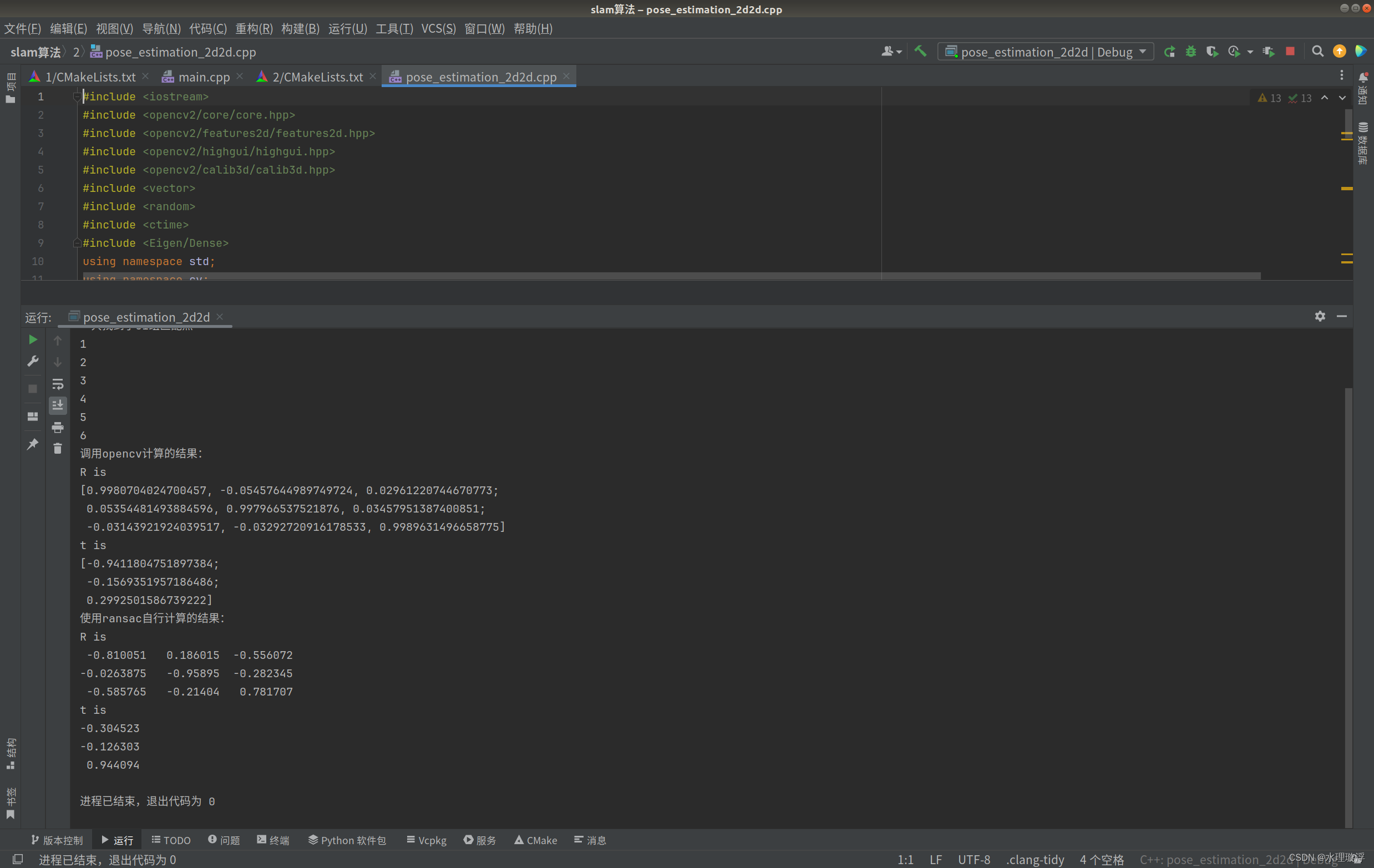
  cout << "调用opencv计算的结果： " << endl;
  cout << "R is " << endl << R << endl;
  cout << "t is " << endl << t << endl;
  cout <<  "使用ransac自行计算的结果： " << endl;
  cout << "R is " << endl << R1 << endl;
  cout << "t is " << endl << t1 << endl;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1805692.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

数据结构笔记 4 树和二叉树

数据结构笔记 4 树和二叉树

二叉树和完全二叉树的区别&#xff1f; 二叉树和完全二叉树的主要区别在于它们的结构特性和节点排列方式&#xff1a; 1. **二叉树**&#xff1a; - 是一种数据结构&#xff0c;其中每个节点最多有两个子节点&#xff0c;通常称为左子节点和右子节点。 - 节点的子节点数量…
阅读更多...
海思SD3403,SS928/926,hi3519dv500,hi3516dv500移植yolov7,yolov8（21）Yolov9s测试

海思SD3403,SS928/926,hi3519dv500,hi3516dv500移植yolov7,yolov8（21）Yolov9s测试

四天前yolov9的作者终于开源了yolov9s和yolov9t模型。这个作者之前一直没开源t,s，只有c开始的，而且onnx转换后数据大小特别大，当时直接就放弃测试了。 另外之前代码有很明显的抄v5的痕迹。所以印象很不好。 现在总算是开源t,s模型，而且这里评估的结果上来看是好于yolov8的…
阅读更多...
两款好用的IOS、Android图片处理应用

两款好用的IOS、Android图片处理应用

GIF 小助手 GIF工具包是一个简单实用的GIF动画编辑器&#xff0c;目前仅支持IOS平台。 使用该软件&#xff0c;可以将多个图像、视频和现场照片创建为gif。 主要功能&#xff1a; 多种输入源&#xff1a;用户可以将多个图片、视频或Livephoto转换成GIF动图。 编辑功能&#…
阅读更多...
RDK X3（aarch64） 测试激光雷达思岚A1

RDK X3（aarch64） 测试激光雷达思岚A1

0. 环境 - 亚博智能的ROSMASTER-X3 - RDK X3 1.0 0.1 资料 文档资料 https://www.slamtec.com/cn/Support#rplidar-a-series SDK https://github.com/slamtec/rplidar_sdk ROS https://github.com/slamtec/rplidar_ros https://github.com/Slamtec/sllidar_ros2 1. robostu…
阅读更多...
windows上安装MongoDB，springboot整合MongoDB

windows上安装MongoDB，springboot整合MongoDB

上一篇文章已经通过在Ubuntu上安装MongoDB详细介绍了MongoDB的各种命令用法。 Ubuntu上安装、使用MongoDB详细教程https://blog.csdn.net/heyl163_/article/details/133781878 这篇文章介绍一下在windows上安装MongoDB&#xff0c;并通过在springboot项目中使用MongoDB记录用户…
阅读更多...
Java：112-SpringMVC的底层原理（下篇）

Java：112-SpringMVC的底层原理（下篇）

这里继续续写上一章博客&#xff08;111章博客&#xff09;&#xff1a; Spring MVC 源码深度剖析&#xff1a; 既然我们自行写出了一个&#xff0c;那么我们可以选择看看mvc源码&#xff1a; 前端控制器 DispatcherServlet 继承结构&#xff1a; 前面我们知道mvc是操作同…
阅读更多...
实验六、IPv4 地址的子网划分，第 2 部分《计算机网络》

实验六、IPv4 地址的子网划分，第 2 部分《计算机网络》

你有没有发现&#xff0c;困的时候真的清醒不了。 目录 一、实验目的 二、实验内容 三、实验小结 一、实验目的 完成本练习之后&#xff0c;您应该能够确定给定 IP 地址和子网掩码的子网信息。 知道 IP 地址、网络掩码和子网掩码后&#xff0c;您应该能够确定有关该 IP 地…
阅读更多...
【学术小白成长之路】02三方演化博弈（基于复制动态方程）期望与复制动态方程

【学术小白成长之路】02三方演化博弈（基于复制动态方程）期望与复制动态方程

从本专栏开始&#xff0c;笔者正式研究演化博弈分析&#xff0c;其中涉及到双方演化博弈分析&#xff0c;三方演化博弈分析&#xff0c;复杂网络博弈分析等等。 先阅读了大量相关的博弈分析的文献&#xff0c;总结了现有的研究常用的研究流程&#xff0c;针对每个流程进行拆解。…
阅读更多...
cmake使用make和Ninja构建对比

cmake使用make和Ninja构建对比

前提 make和Ninja是两个常见的构建工具&#xff0c;在网上查阅了一些资料&#xff0c;说是Ninja比make构建速度要快很多。但是具体不知道快多少&#xff0c;所以趁着这次编译clang的机会&#xff0c;分享下它们在时间方面差多少。 步骤 下载llvm 参考llvm官网&#xff0c;这…
阅读更多...
Shell脚本学习_内置命令

Shell脚本学习_内置命令

目录 1.内置命令介绍&#xff1a; 2.Shell内置命令&#xff1a;alias设置别名 3.Shell内置命令&#xff1a;echo输出字符串 4.Shell内置命令&#xff1a;read读取控制台输入 5.Shell内置命令&#xff1a;exit退出 6.Shell内置命令&#xff1a;declare设置变量 1.内置命令…
阅读更多...
详解SM3算法加密流程（SM3加密算法一）

详解SM3算法加密流程（SM3加密算法一）

1、SM3 算法简介 SM3是中国国家密码管理局发布的消息摘要算法&#xff0c;首次发布于2010年&#xff0c;并于2016年发布了正式的国家标准GB/T 32905-2016。类似于国际上广泛应用的SHA-256算法&#xff0c;但有其独特的设计和实现细节。 该算法应用于各种数据加密和验证场景&…
阅读更多...
【NI国产替代】产线综测仪：锂电池保护板测试仪，支持快速定制

【NI国产替代】产线综测仪：锂电池保护板测试仪，支持快速定制

• 精度等级01% • 支持直流电压、电流、nA 级待机电流电阻等&#xff0c;常规测试 • 支持过压、欠压、过冲、过放、过温,短路等&#xff0c;保护测试 • 通讯总线电平可编程&#xff0c;兼容多种 • 支持 SWD 或IIC 固件烧录 • 测试速度快&#xff0c;支持最多 24 通道…
阅读更多...
Windows关闭自动更新最有效的方法

Windows关闭自动更新最有效的方法

按WR打开电脑命令框输入“regedit”进入注册表 依次点击以下几个 右击新建一个“DWORD(32位)值”&#xff0c;命名为”FlightSettingsMaxPauseDays“ 右边选择十进制&#xff0c;左边填写暂停更新的天数 打开windows更新&#xff0c;进入高级选项 选择暂停更新的天数&#xff…
阅读更多...
数据库(27)——多表查询——自连接

数据库(27)——多表查询——自连接

语法 SELECT 字段列表 FROM 表A 别名A JOIN 表A 别名B ON 条件...; 自连接可以是内连接查询也可以是外连接查询。 演示 我新增了字段friend便于演示 查询所有人的名字以及他们的friend的人的名字&#xff1a; select a.name,b.name from user a,user b where a.friendb.id; 其…
阅读更多...
L48---1637. 两点之间不包含任何点的最宽垂直区域(排序）---Java版

L48---1637. 两点之间不包含任何点的最宽垂直区域(排序）---Java版

1.题目描述 2.思路 &#xff08;1&#xff09;返回两点之间内部不包含任何点的 最宽垂直区域 的宽度。 我的理解是相邻两个点&#xff0c;按照等差数列那样&#xff0c;后一个数减去相邻的前一个数&#xff0c;才能保证两数之间不含其他数字。 &#xff08;2&#xff09;所以&…
阅读更多...
kali2022安装教程（附安装包）

kali2022安装教程（附安装包）

第一步&#xff1a;下载镜像文件 百度网盘下载https://pan.baidu.com/s/1efRQGFTbq6Kgw9axLOmWzg?pwdemxf 第二步&#xff1a;打开Vmware 第三步&#xff1a;进行各项配置 创建新的虚拟机&#xff0c;选择高级&#xff0c;然后下一步 直接默认下一步 选择稍后安装然后下…
阅读更多...
CUDA 编程(1):使用Grid 和 Block分配线程

CUDA 编程(1):使用Grid 和 Block分配线程

1 介绍 1.1 Grid 和 Block 概念 核函数以线程为单位进行计算的函数，cuda编程会涉及到大量的线程(thread),几千个到几万个thread同时并行计算，所有的thread其实都是在执行同一个核函数。 对于核函数(Kernel),一个核函数一般会分配1个Grid, 1个Grid又有很多个Block，1个Bloc…
阅读更多...
IO流(缓冲流)

IO流(缓冲流)

1.字节缓冲流 原理&#xff1a;字节缓冲输入流自带8KB缓冲池;字节缓冲输出流自带8KB缓冲池 public static void main(String[] args) throws IOException {try(InputStream is new FileInputStream("D:\\pt\\123.jpg");//1.定义一个字节缓冲输入流包装原始的字节输…
阅读更多...
看似不同的事情，却是相同的坑

看似不同的事情，却是相同的坑

目录 一、背景二、过程1.遭遇战-微盘股的下杀2.不失为一件好事3.一切向后看吧&#xff0c;最近的学习感受4.该有的心境 三、总结 一、背景 也在一点点改变&#xff0c;期间势必要经历流血的过程&#xff1b;所谓无疯狂不成长&#xff0c;积极的心态去应对&#xff0c;去总结总…
阅读更多...
数据分析常用模型合集（一）AARRR模型和漏斗模型

数据分析常用模型合集（一）AARRR模型和漏斗模型

准备把常用的数据分析模型&#xff0c;像什么AARRR&#xff0c;RFM之类的&#xff0c;逐个全部写一下&#xff1b; 最好能带点案例和代码&#xff0c;搞一个小合集。 最终达到完全不懂的人&#xff0c;看完就能知道得差不多&#xff1b; 数据分析常用模型合集&#xff08;二…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023