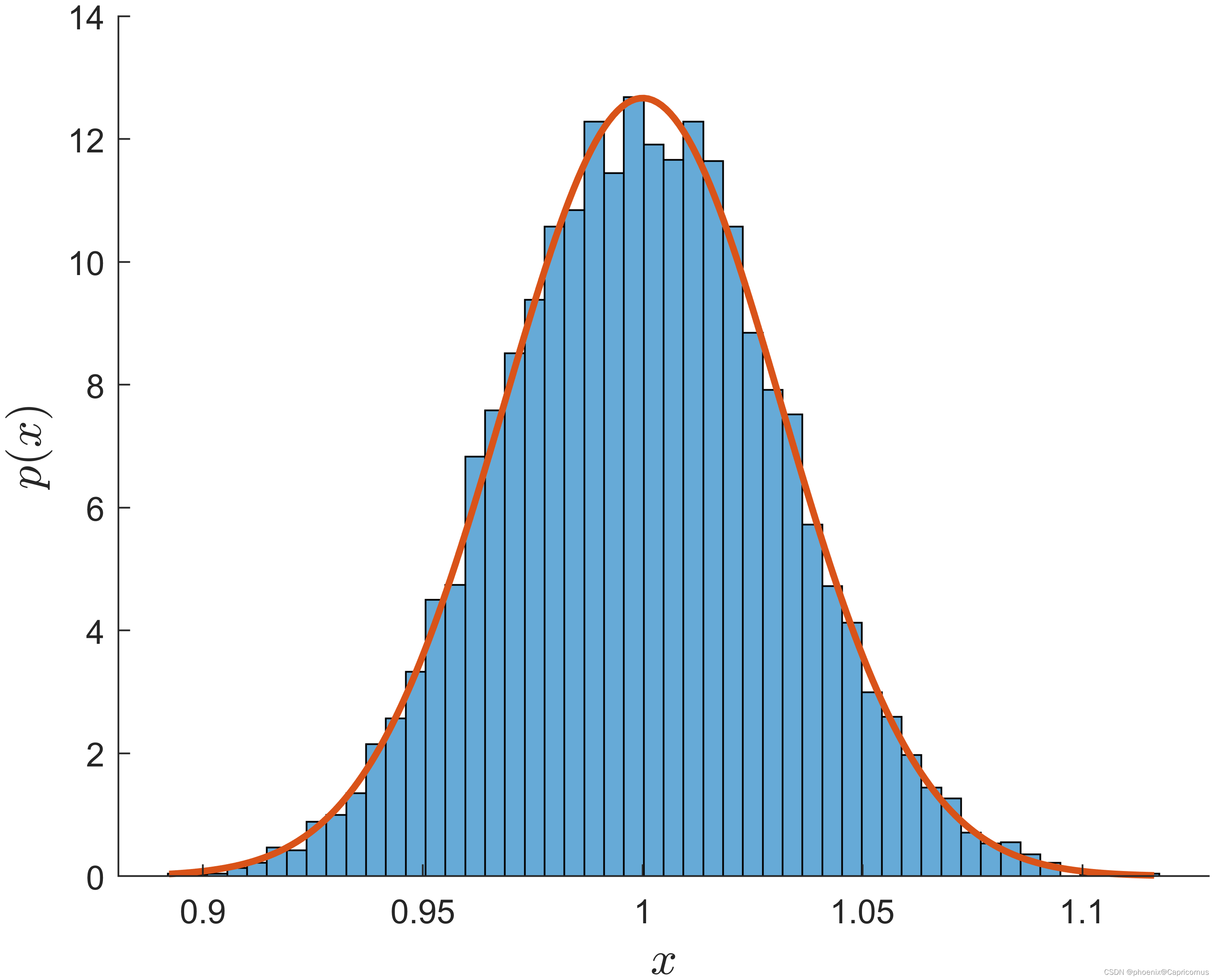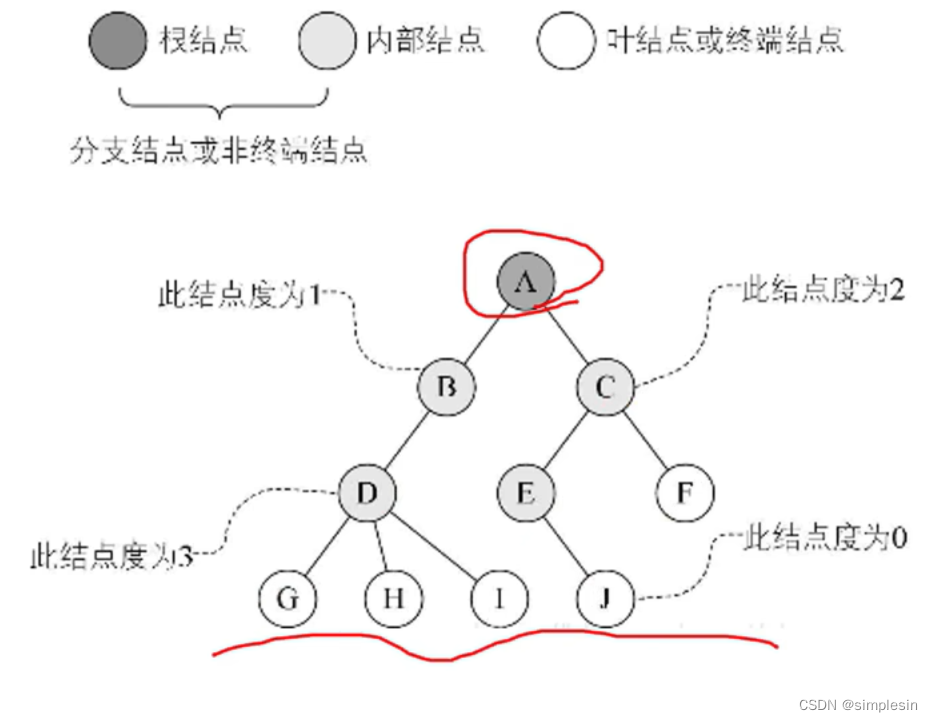



二叉树和完全二叉树的区别?
二叉树和完全二叉树的主要区别在于它们的结构特性和节点排列方式:
1. **二叉树**:
- 是一种数据结构,其中每个节点最多有两个子节点,通常称为左子节点和右子节点。
- 节点的子节点数量可以是0、1或2,没有特定的排列要求,因此二叉树可以呈现各种形状,包括斜树、满二叉树、完全二叉树等。
- 不强制所有层级都要填满,也不要求最后一层的节点必须集中在左边。2. **完全二叉树**:
- 是二叉树的一个特殊形态,除了最后一个层级外,所有层级都被完全填满。
- 最后一层的节点都尽可能地集中在左侧。如果最后一层没有被填满,那么所有节点都必须靠左排列,不能有空位在某个节点的右侧而该节点有后代。
- 具有n个节点的完全二叉树的深度最小,也就是说,它是高度最矮的能够包含n个节点的二叉树。
- 完全二叉树在某些情况下便于实现数据结构(如堆)和算法(如二分查找),因为它们的结构更加规则。

几种遍历方式: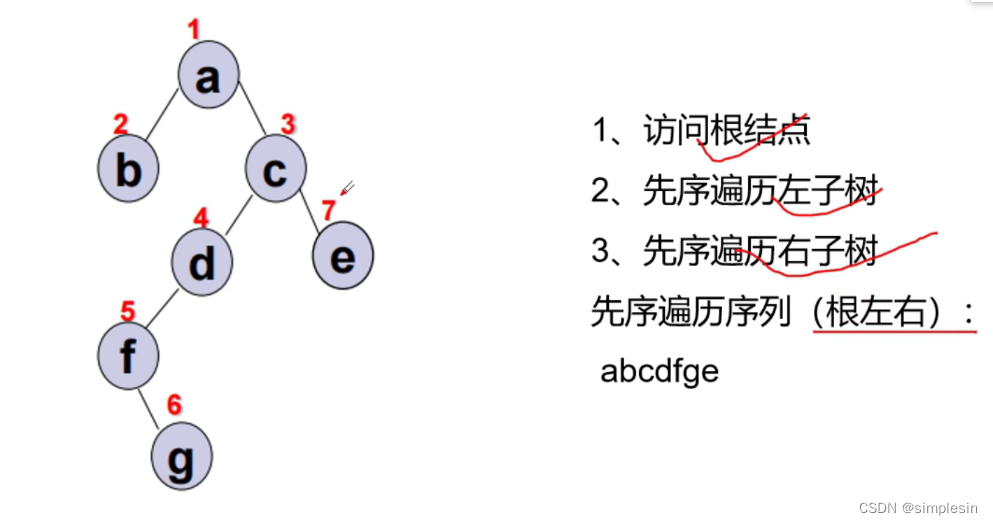

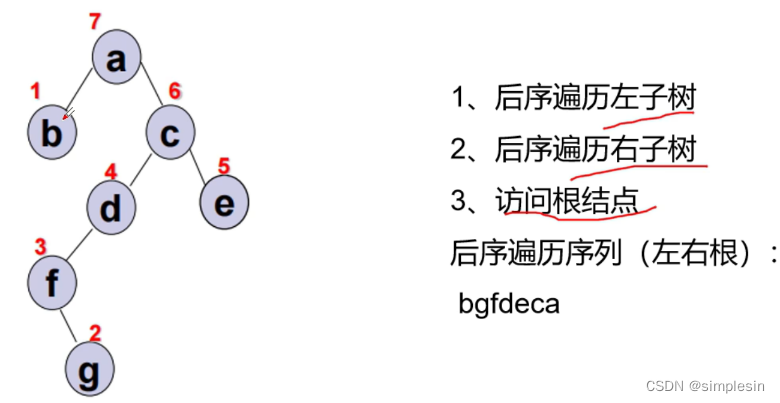


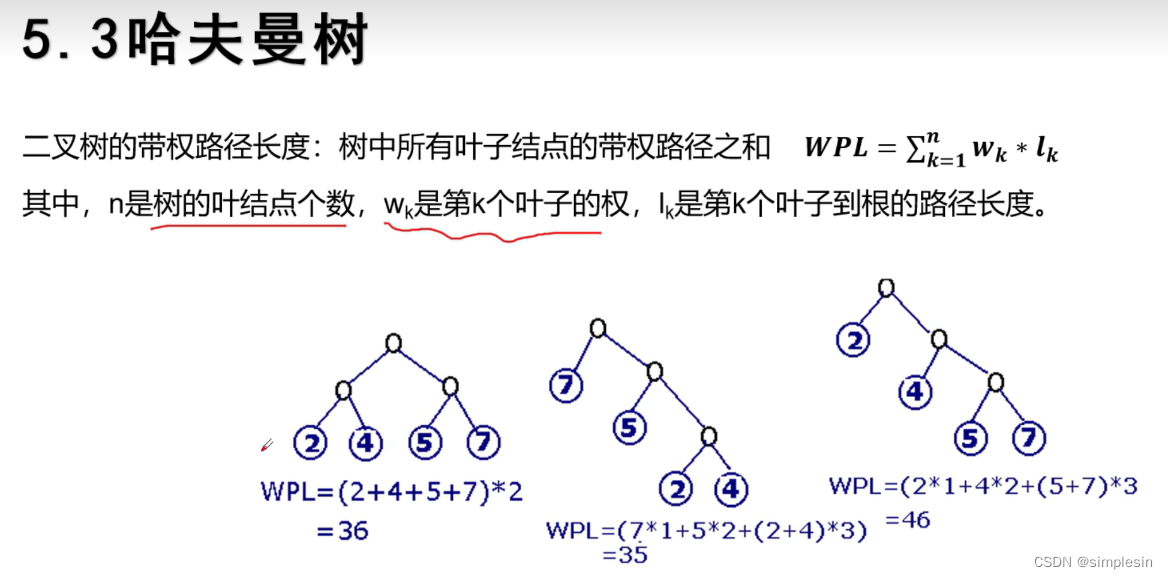
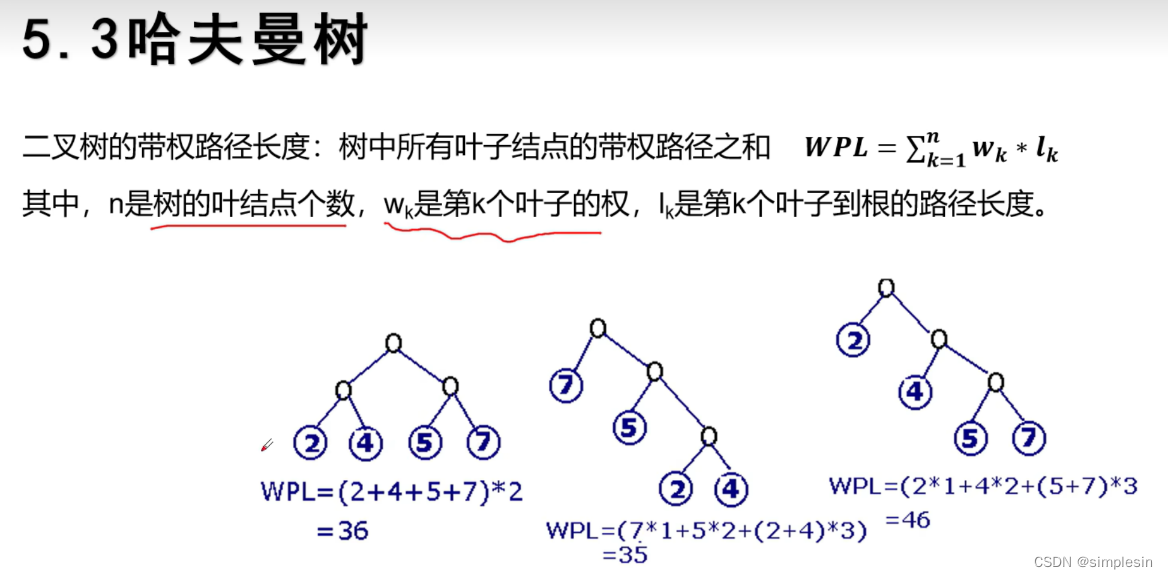 构造哈夫曼树
构造哈夫曼树