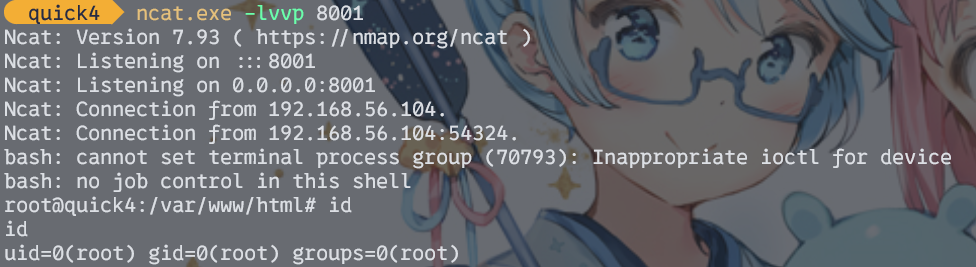
1.基础作业

1.1配置 LMDeploy 运行环境

创建开发机

创建新的开发机，选择镜像Cuda12.2-conda；选择10% A100*1GPU；点击“立即创建”。注意请不要选择Cuda11.7-conda的镜像，新版本的lmdeploy会出现兼容性问题。其他和之前一样，不赘述。

创建conda环境

studio-conda -t lmdeploy -o pytorch-2.1.2

安装LMDeploy

#激活虚拟环境
conda activate lmdeploy
#安装0.3.0的imdeploy
pip install lmdeploy[all]==0.3.0

1.2以命令行方式与 InternLM2-Chat-1.8B 模型对话

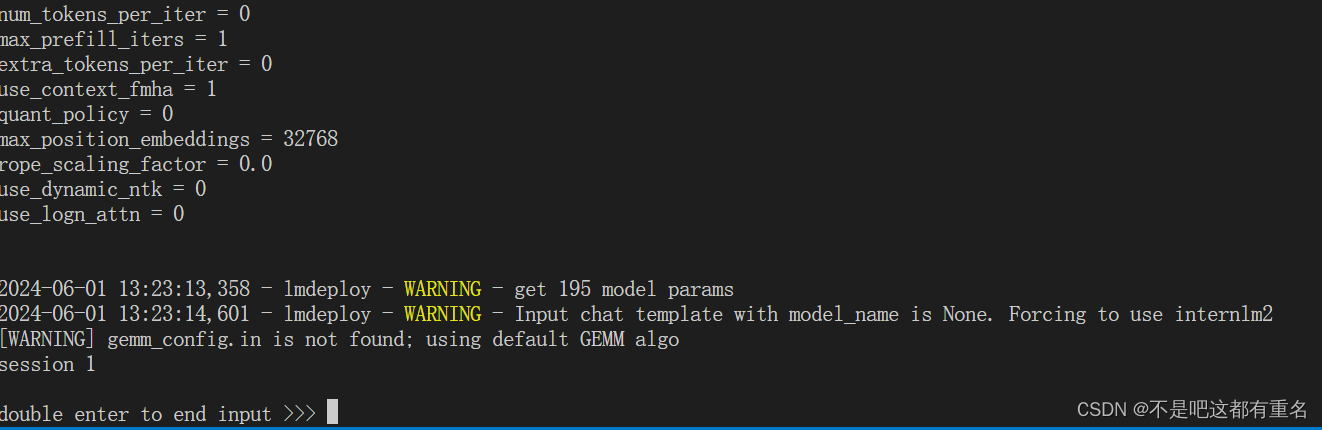
2.进阶作业

2.1 设置KV Cache最大占用比例为0.4，开启W4A16量化，以命令行方式与模型对话。

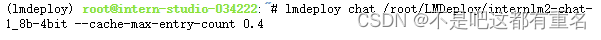
2.2 以API Server方式启动 lmdeploy，开启 W4A16量化，调整KV Cache的占用比例为0.4，分别使用命令行客户端与Gradio网页客户端与模型对话。

命令行：


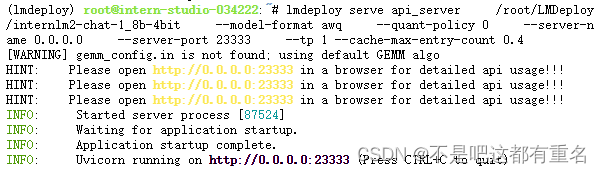
网页客户端：

2.3 使用W4A16量化，调整KV Cache的占用比例为0.4，使用Python代码集成的方式运行internlm2-chat-1.8b模型。

2.4 使用 LMDeploy 运行视觉多模态大模型 llava gradio demo。