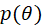- 💭 写在前面:本章我们将介绍 F# 的模块,我们前几章讲的列表、集合和映射都是模块。然后我们将介绍 F# 中的异常,以及内置异常,最后再讲解一下相互递归函数。
目录
0x00 F# 模块(Module)
0x01 F# 异常处理(Exception)
0x02 内置异常(Built-in Exceptions)
0x03 相互递归函数
0x04 通过泰勒级数展开来逼近计算 e^x
0x00 F# 模块(Module)
用于代码组织和抽象的特性,模块 (Module) 就是相关类型、值和函数的集合。
类似于面向对象编程中的类,但没有对象的概念。
比如我们说的的列表、集合和映射都是模块。
在这个章节后,我会给出一点练习题,方便大家更好地掌握 F# 基础。
为了方便大家没有负担地有效练习,我会在框架代码中勾勒出模块,你只需要填写就行了:
namespace DataStructure
module Queue =
type t = int list * int list
let empty: t = ([], [])
let enqueue (i: int) (queue: t) = ...另外,这个 namespace 就是命名空间,类似于 C++。
0x01 F# 异常处理(Exception)
F# 中也是可以 raise 捕获异常的,raise ... 会被求值为一个异常并传播。
使用 try-with 来捕获引发的异常,异常会被视为 any type,可以是任何类型 ( `a ) 。
exception DivByZero
let div (x: int) (y: int) : int =
if y = 0 then raise DivByZero else x / y
let printDiv (x: int) (y: int) : unit =
try printfn "%d" (div x y) with
| DivByZero -> printfn "Divisor is zero" 0x02 内置异常(Built-in Exceptions)
F# 有不少预定义的异常,要捕获这些错误,你必须使用 |:?
这是因为 F# 与 C# (.NET) 都是一个爹有着密不可分的关系。
这里提供几种还不错的选择,让你避免记住这些复杂的异常名称:
let doFind1 (k: string) (m: Map<string,int>) : int =
try Map.find k m with
| :? System.Collections.Generic.KeyNotFoundException -> 0
let doFind2 (k: string) (m: Map<string,int>) : int =
if Map.containsKey k m then Map.find k m else 0
let doFind3 (k: string) (m: Map<string,int>) : int =
match Map.tryFind k m with
| None -> 0 | Some i -> i0x03 相互递归函数
相互递归函数 (Mutually Recursive Function),指的是多个函数可以相互递归调用。
简单来说就是你递归调用我,我递归调用你,用 let rec ... and 语法来定义这样的函数。
💬 举个例子:我们来定义三个相互递归的函数
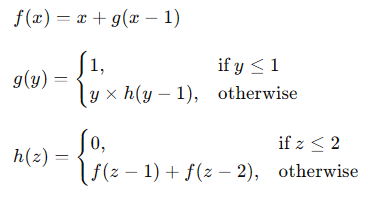
let rec f x =
x + g (x - 1)
and g y =
if y <= 1 then 1 else y * h (y - 1)
and h z =
if z <= 2 then 0 else f (z - 1) + f (z - 2)这段代码定义了三个相互递归的函数 ,它们彼此之间互相调用。
形成了一个循环,每个函数的返回值都依赖于其他函数的返回值,从而实现了相互递归。
0x04 通过泰勒级数展开来逼近计算 e^x
通过泰勒级数展开来逼近计算 。
① 首先计算 的阶乘:
我们定义一个递归函数 Fac 计算一个非负整数的阶乘,当输入值 时,返回1。
否则,返回 乘以
的阶乘。
在 Tylor 函数中,Fac 被用来计算泰勒级数展开的分母部分,即 。
② 再通过泰勒级数展开公式 (以 为底的指数函数) ,我们展开前十项:
再定义一个递归函数 Taylor 计算 的泰勒级数展开,当展开的级数项数
时,返回
。
否则计算 并加上递归调用 T
aylor 函数计算更低阶的项。
在 Taylor 函数中,Fac 函数被用来计算每一项的阶乘。
💬 代码演示:通过泰勒级数展开来逼近计算
let rec Fac n =
if n <= 1 then 1
else n * Fac (n - 1)
let rec Taylor x n =
if n = 0 then 1.0
else (float x ** float n) / float (Fac n) + Taylor x (n - 1)
// 计算 e^x 的值
let calculateExponential x =
if System.Double.IsNaN(x) || System.Double.IsInfinity(x) then
invalidArg "x" "x must be a finite number"
else
Taylor x 10 // 前10项这两个函数就相互递归了,因为 Taylor 调用了 Fac 来计算阶乘,而 Fac 也会调用 Taylor。
你可以发现,我们没有使用刚才讲的 "0x03 相互递归",let rec ... and。
因为每次计算阶乘都会重新计算泰勒级数的一部分,导致大量的重复计算:
let rec Fac n =
if n <= 1 then 1
else n * Taylor (n - 1) 1
and Taylor x n =
if n = 0 then 1.0
else (float x ** float n) / float (Fac n) + Taylor x (n - 1)
// 计算 e^x 的值
let calculateExponential x =
if System.Double.IsNaN(x) || System.Double.IsInfinity(x) then
invalidArg "x" "x must be a finite number"
else
Taylor x 10 // 前10项
// 测试计算函数
let result = calculateExponential 1.0
printfn "e^1 的值近似为: %f" result
📌 [ 笔者 ] 王亦优
📃 [ 更新 ] 2024.6.16
❌ [ 勘误 ] /* 暂无 */
📜 [ 声明 ] 由于作者水平有限,本文有错误和不准确之处在所难免,
本人也很想知道这些错误,恳望读者批评指正!| 📜 参考资料 Microsoft. MSDN(Microsoft Developer Network)[EB/OL]. []. . |