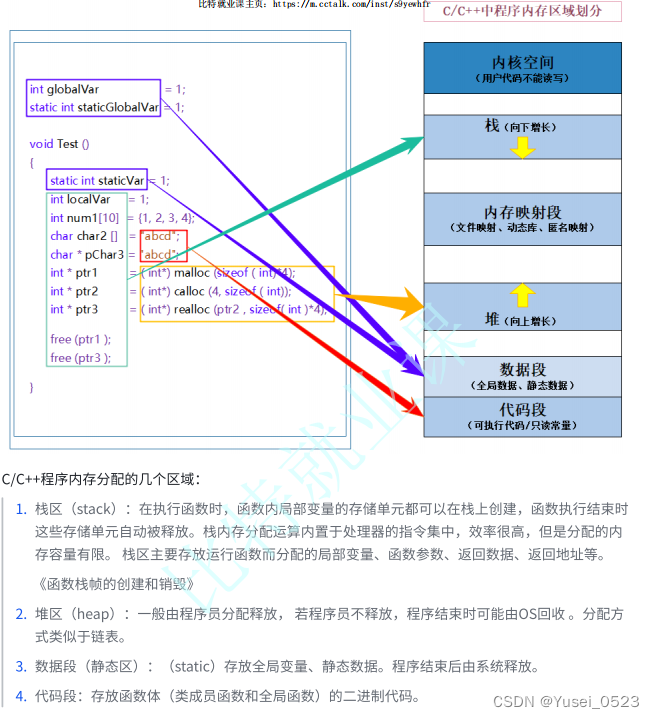
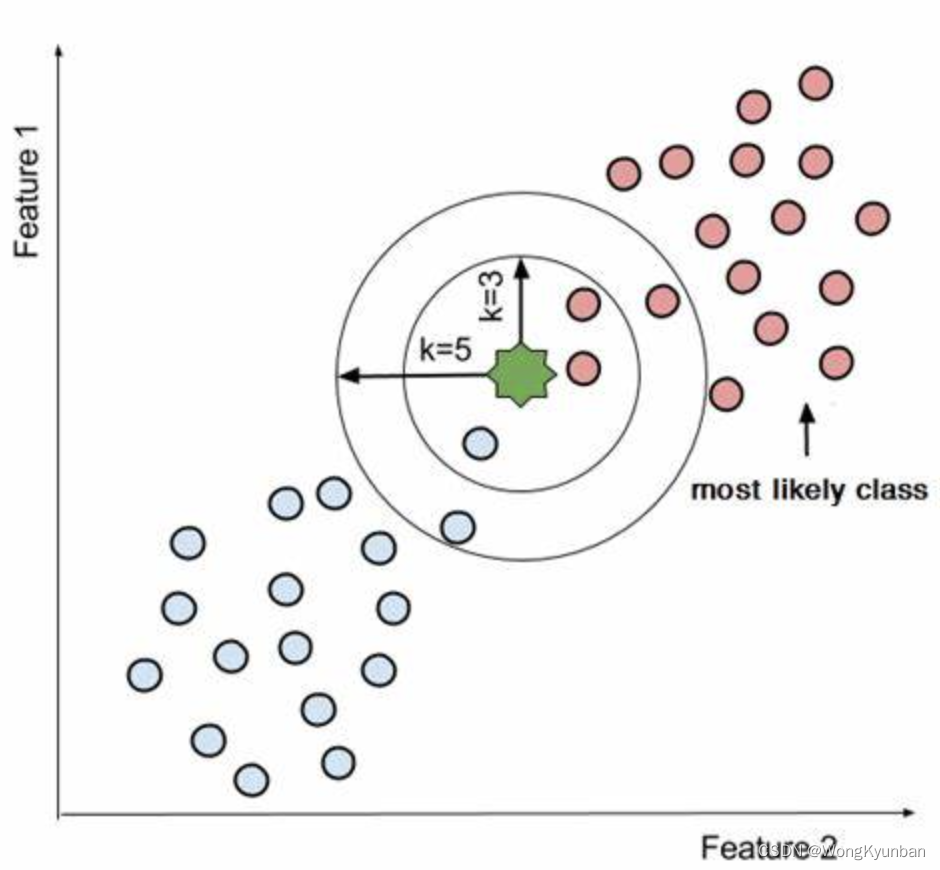
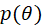注： 判断两函数是否相同，只看定义域和对应法则。

1. 函数的定义

    一般的，在一个变化过程中有两个变量 x，y。如果对于x在某个变化范围内的每一个确定值，按照某个对应法则，都有唯一确定的值y和他对应。那么y就是x的函数，x叫做自变量，y叫做因变量。可以记作 y = f(x) 其中，f表示对应法则。

2. 函数的表示方法

• 解析法：用等式表示两个变量间函数关系的方法。如 y = 2x +  3；
• 列表法：用表格表示两个变量间函数关系的方法。
• 图像法：用图像表示两个变量间函数关系的方法。

3. 常见的函数定义域

1. f(x) 是整数时，定义域是全体实数。
2. f(x) 是分式函数时，分母不能为0。
3. f(x) 是偶次方根时，被开方数大于等于0。若为奇次方根，则被开方数无要求。0的0次方无意义。
4. 对数函数的真数大于0。
5. 对数函数或指数函数的底数大于0且不等于1。
6. 在y = tan x 中， x ≠ kΠ + Π/2 （k 属于Z）。
7. 若是有几个式子构成的，则定义域为这几个式子定义域的交集。

4. 函数的单调性

1. 函数单调性的定义

    在一个区间上，如果自变量X的任意两个值，x1、x2，当x1 ＜ x2时，都有 f（x1） 小于 f（x2）那么称f(x)在此区间上是增函数；但若 f(x1) ＞ f(x2)，那么称该函数在此区间上是减函数。

如果函数y = f(x) 在某区间上是增函数/减函数，就说 f(x) 在此区间上具有单调性，在此区间叫做f(x)的单调区间。

2. 函数单调性的图像特征

3. 函数单调性的判断方法

1. 设x1，x2是定义域活区间D上的任意两个值，且x1＜x2。
2. 做差 f(x1) - f(x2)，并将差的形式化简，目标是有利于判断结果的正负号。
3. 判断 f(x1) - f(x2) 的正负。
4. 得出结论。

5. 函数的奇偶性

1.函数奇偶性的定义

设y = f(x)，在其定义域内任取一点，且 -x 也在其定义域内。

1. 若 f(x) = f(-x),则称函数f(x)为偶函数。
2. 若 f(-x) = -f(x) 则成函数f(x)为奇函数。

2. 函数奇偶性的图像特征

• 奇函数的图像关于原点对称。
• 偶函数的图像关于y轴对称。

3. 奇偶性四则运算

1. 奇函数 + 奇函数 = 奇函数
2. 偶函数 + 偶函数 = 偶函数
3. 奇函数 + 偶函数 = 非奇非偶函数
4. 奇函数 * 奇函数 = 偶函数
5. 偶函数 * 偶函数 = 偶函数
6. 奇函数 * 偶函数 = 奇函数