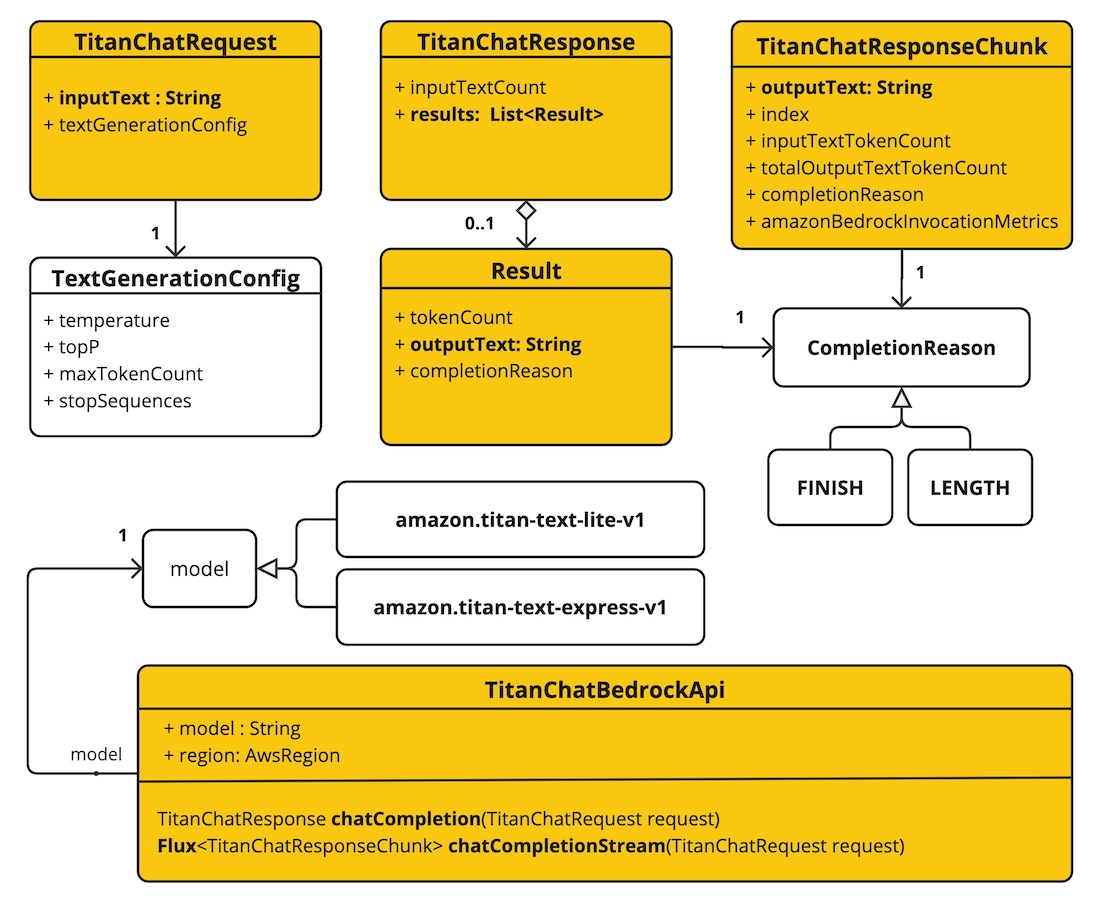
所谓kNN算法就是K-nearest neigbor algorithm。这是似乎是最简单的监督机器学习算法。在训练阶段,kNN算法存储了标签训练样本数据。简单地说,就是调用训练方法时传递给它的标签训练样本会被它存储起来。
kNN算法也叫lazy learning algorithm懒惰学习算法。因为在训练阶段传递给它的训练样本会延迟到预测阶段处理。换句话说,对于kNN算法,训练阶段的方法调用只是为了把训练样本存储到模型中而已,不会做什么具体的训练。这也是由它的算法特点决定。
在预测阶段,kNN算法会找到离查询点(预测点)最近的k个点,然后统计这个k个点的标签,最后以标签最多的结果作为查询结果。
所以kNN算法并没有训练的阶段。所以它计算预测点到样本点的距离的工作,只能够延迟到预测阶段,用来传入的查询点来完成计算。
kNN算法的预测是基于查询点到样本点的比较。所以在预测时,它的所有样本点必须加载到内存中,没有样本点,kNN算法是无法工作的,所以kNN又叫懒惰的基于实例(基于内存)算法。
在继续往下说前,我们先来了解两个概念:离散数据和连续数据,它们都是量化数据的类型,主要的区别在于它们所表示的信息类型。离散数据通常仅仅表示特定事件的信息,而连续数据通常表示随着时间变化的趋势。
- 离散数据通常是一个确切的数字,我们能够数出来的,例如,一个班级的学生人数,鞋子的尺寸。相反,连续数据通常包括表示一系列信息的可测量值,如房价、股票价格。离散值是一个特定值,而连续值可以是任意值。
- 在一个特定时间区间中,离散数据是一个常量,而连续数据则有多个不同的值。比如股价在交易时段中,价格就会一直在变化,可能会出现许多不同的价格,这是典型的连续数据。
kNN机器学习可以解决两大类问题:分类问题和回归问题。因为kNN算法会携带着训练数据来做预测,因此当数据集变得很大时,它的性能就会下降得很快。kNN算法一般用于一些简单的推荐系统、模式识别、数据挖掘、金融市场的预测、入侵检测等等。
kNN算法的距离度量问题
这个问题主要是解决哪些数据点离我们要查询的数据点比较近。所以查询数据点与其他数据点的距离是需要先算出来的。这个距离的度量有效地帮助我们形成决策的范围,简单来说就是帮我们找到那k个最近的点。
分类问题
对于分类问题,它是根据多数票来分配类别标签的。首先,用kNN算法构建的模型,要确定它要对什么东西分类,有多少类,然后将这些分类数据构建出来:一个样本数据包括了特征和标签数据,当这些数据给到模型训练时,它们都是一一对应的。这样模型才能基于正确的特征和对应的标签找到一个映射的方法(函数)完成输入到输出的映射。
这个多数票是怎么来的呢?首先kNN中的k代表了我们要从训练数据(kNN算法是一个用训练数据去做预测的算法)中找离我们要预测的数据点(这个数据点,我们只提供特征数据,目的是想让模型告诉我们,它属于哪个分类)最近的k个点,这k个数据点它们的分类可能是不同的,于我们对它们的分类标签进行统计(计票),最终的结果就是以票数多的数据点的分类标签作为这一次的预测结果。
在kNN算法中,我们还可以对于计票结果作一些要求,比如说如果分类类别只有两种的话,可以要求票数必须超过50%,如果是4个分类的话,可以要求票数必须超过25%。
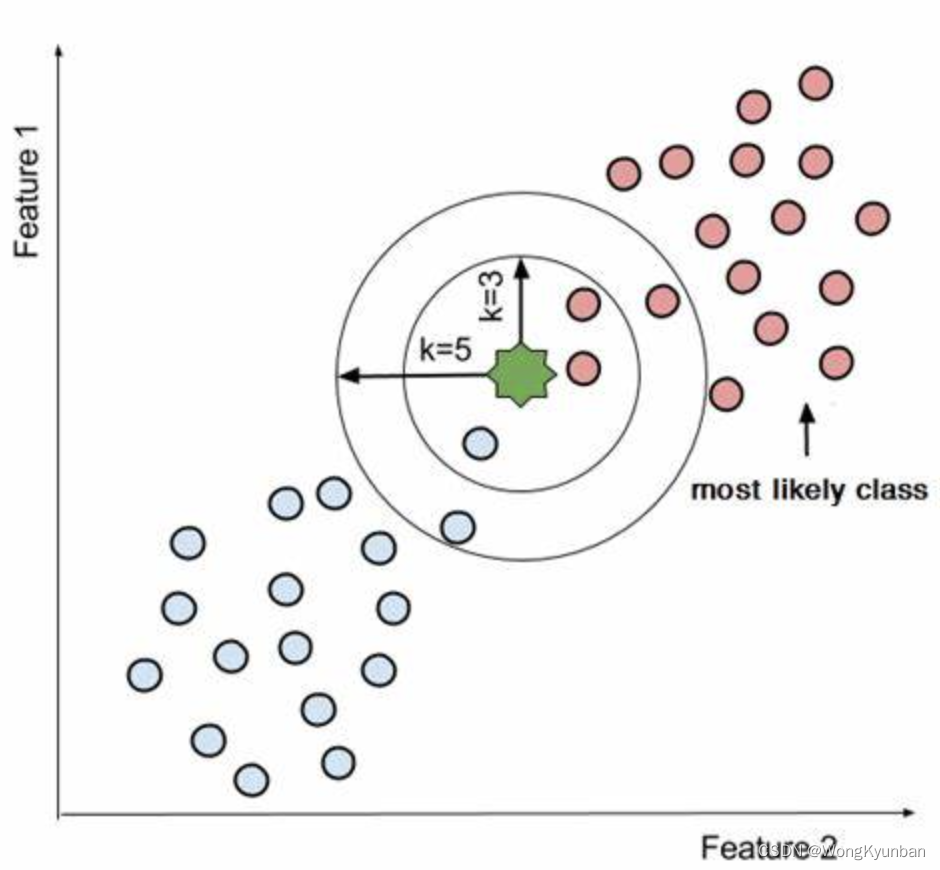
在完成一个分类的预测前,我们要用到欧几里德距离来确定预测点与训练数据集中的点的距离,以此找出k个距离最近的点。
回归(Regression)问题
Regression,回归,“the act of going back,回去的行为",所以回归问题就是通过找到预测的数据(没有见过的数据,未知的数据)与过去已知数据的关系,以此来预测当前的数据点。房价预测、股价预测都是很典型的例子。
回归问题和分类问题很类似。区别在于分类问题是用于离散数据的,而回归问题则是用于连续数据的。
我们先说这么多先。后面继续介绍。