单源最短路径算法 -- 迪杰斯科拉（Dijkstra）算法

news2024/11/27 10:32:16

1. 简介

迪杰斯科拉（Dijkstra）算法是一种用于在加权图中找到最短路径的经典算法。它是由荷兰计算机科学家Edsger Wybe Dijkstra在1956年首次提出的，并以他的名字命名。这个算法特别适合于解决单源最短路径问题，即计算图中一个顶点到其他所有顶点的最短路径。

2. 核心原理

Dijkstra算法的核心很简单，就是贪心算法的思想，它每次都选择当前已知的最短路径，并以此作为基础来更新其他顶点的最短路径估计。

注： Dijkstra算法只能用于图中所有权重为非负数，因为过程中会对路径上的权重进行累加比较。

3. 算法步骤

将源顶点的距离设为0，其他所有顶点的距离设为无穷大。
将源顶点加入已访问集合。
遍历未访问顶点，找出距离最短的顶点，将其加入已访问集合。
更新邻接顶点的距离，如果新计算的距离小于当前距离，则更新距离。
重复步骤3和4，直到所有顶点都被访问过。

4. 图解

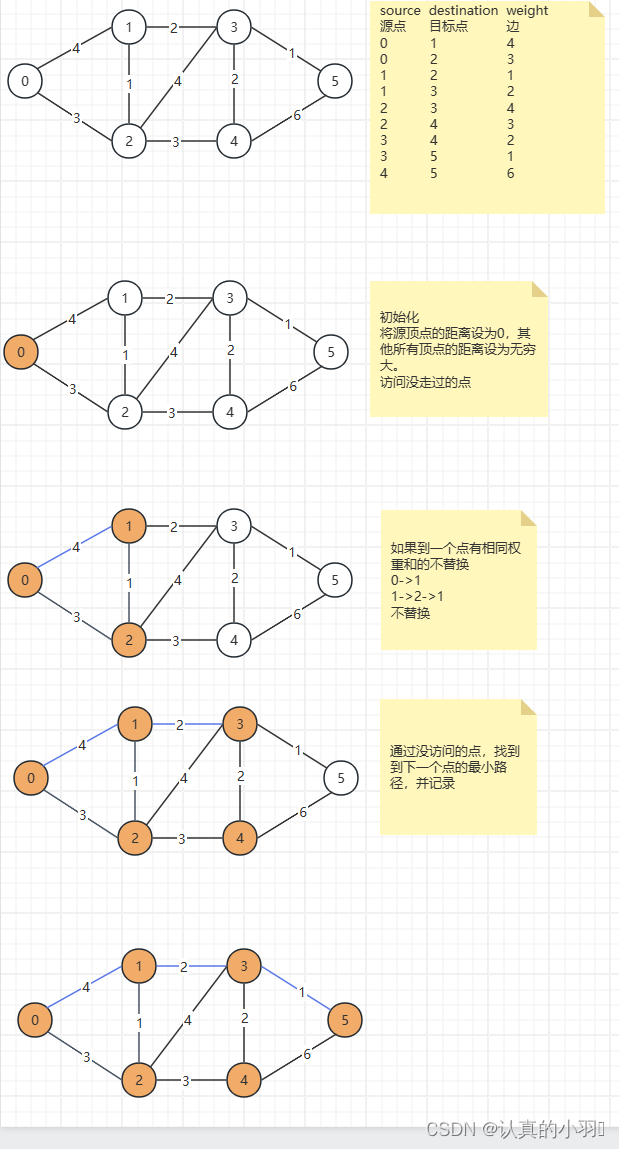
5. 代码实现

class Graph {
    private int vertices;
    private LinkedList<Edge>[] adjacencyList;

    public Graph(int vertices) {
        this.vertices = vertices;
        adjacencyList = new LinkedList[vertices];
        for (int i = 0; i < vertices; i++) {
            adjacencyList[i] = new LinkedList<>();
        }
    }

    // 添加一个边
    public void addEdge(int source, int destination, int weight) {
        Edge edge = new Edge(source, destination, weight);
        adjacencyList[source].addFirst(edge);
    }


    public void dijkstra(int startVertex) {
        boolean[] visited = new boolean[vertices];  // 记录顶点是否被访问过
        int[] distance = new int[vertices];         // 记录起始顶点到其他顶点的最短距离

        // 初始化距离数组
        Arrays.fill(distance, Integer.MAX_VALUE);
        distance[startVertex] = 0;

        // 使用优先队列来维护待访问顶点
        PriorityQueue<Edge> pq = new PriorityQueue<>(Comparator.comparingInt(edge -> edge.weight));
        pq.offer(new Edge(-1, startVertex, 0));

        // 核心
        while (!pq.isEmpty()) {
            Edge edge = pq.poll();
            int currentVertex = edge.destination;
            
            // 如果当前顶点已经被访问过，则跳过
            if (!visited[currentVertex]) {
                visited[currentVertex] = true;

                // 更新相邻顶点的最短距离
                LinkedList<Edge> neighbors = adjacencyList[currentVertex];
                for (Edge neighbor : neighbors) {
                    // 相邻顶点未被访问过
                    if (!visited[neighbor.destination]) {
                        int newDistance = distance[currentVertex] + neighbor.weight;
                        // 如果新的距离小于当前距离，则更新距离
                        if (newDistance < distance[neighbor.destination]) {
                            distance[neighbor.destination] = newDistance;
                            pq.offer(new Edge(currentVertex, neighbor.destination, newDistance));
                        }
                    }
                }
            }
        }

        printShortestPath(distance, startVertex);
    }

    // 打印结果
    private void printShortestPath(int[] distance, int startVertex) {
        System.out.println("Shortest path from vertex " + startVertex + " to all other vertices:");
        for (int i = 0; i < vertices; i++) {
            System.out.println("To vertex " + i + ": " + distance[i]);
        }
    }

    // 边
    static class Edge {
        int source;         // 源点
        int destination;    // 目标点
        int weight;         // 权重

        public Edge(int source, int destination, int weight) {
            this.source = source;
            this.destination = destination;
            this.weight = weight;
        }
    }
}

public class DijkstraAlgorithm {
    public static void main(String[] args) {
        Graph graph = new Graph(6);
        graph.addEdge(0, 1, 4);
        graph.addEdge(0, 2, 3);
        graph.addEdge(1, 2, 1);
        graph.addEdge(1, 3, 2);
        graph.addEdge(2, 3, 4);
        graph.addEdge(2, 4, 3);
        graph.addEdge(3, 4, 2);
        graph.addEdge(3, 5, 1);
        graph.addEdge(4, 5, 6);

        graph.dijkstra(0); // Starting vertex is 0
    }
}

6. 应用场景

路由算法：在路由器中，Dijkstra算法帮助确定经过哪些中间节点可以最快地传输数据包。尽管现代互联网路由器采用的协议更为复杂，但这些协议的核心仍然是基于Dijkstra算法的。
交通规划：在城市交通网络中，通过Dijkstra算法计算最短路径，可以设计更有效的交通网络，减少拥堵并提高效率。尽管实际的规划功能可能会使用更复杂的算法来考虑交通状况、路况等因素，Dijkstra算法的基本思想仍然被广泛应用。
社交网络：在社交网络分析中，Dijkstra算法可以帮助识别人与人之间的最短联系链。例如，在一个社交网络中，想要找到连接两个特定用户的最短关系链时，Dijkstra算法能够派上用场。这在实现某些社交功能，如“你可能认识的人”推荐时非常有用。
通信网络设计：设计电话网络或有线电视网络时，Dijkstra算法可以帮助确定最佳的电缆或光纤布线路径，以最小化成本同时保证服务质量。这是通过计算中心节点（如交换机或分配器）到所有其他节点的最短路径来实现的。