NGINX之location和rewrite

news2024/11/27 11:40:54

一.NGINX常用的正则表达式

二.Location

location作用:对访问的路径做访问控制或者代理转发

1.location 常用的匹配规则：

=	进行普通字符精确匹配，也就是完全匹配
^~ /	表示普通字符匹配。使用前缀匹配。如果匹配成功，则不再匹配其它正则匹配location。
~ /	区分大小写的匹配。
~*	不区分大小写的匹配。
!~	区分大小写的匹配取非。
!~*	不区分大小写的匹配取非。

location 大致可以分为三类：
精准匹配：location = / {...}
一般匹配：location / {...} 一般匹配先匹配前缀匹配，最后在用通用匹配
正则匹配：location ~ / {...}

2.location匹配机制：

优先级：精准匹配 = > 最长前缀匹配 ^~ > 正则匹配 ~ ~* !~ !~* > 一般前缀匹配 /XXXX > 通用匹配 /

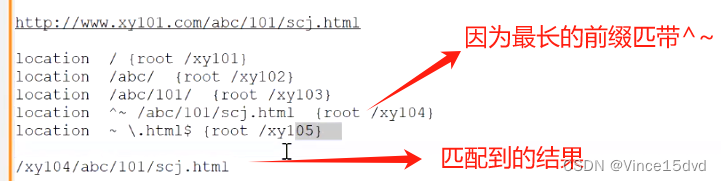
意思：在没有精准匹配的情况下，先看最长的前缀匹配，取最长的前缀匹配，如果最长前缀匹配有^~则不继续看正则匹配了，如果最长前缀匹配没^~就要继续看正则匹配，匹配到及停止。

前缀匹配看长度，最长的优先匹配；正则匹配看上下顺序，根据nginx配置文件的配置由上往下依次匹配，匹配到即停止
案例：

三.Rewrite

rewrite的作用是：对访问的域名或者域名内的URL路径地址重写
rewrite功能就是：使用nginx提供的全局变量或自己设置的变量，结合正则表达式和标记位实现URL重写以及重定向。
比如：更换域名后需要保持旧的域名能跳转到新的域名上、某网页发生改变需要跳转到新的页面、网站防盗链等等需求。

注意：rewrite只能放在server{},location{},if{}中，并且默认只能对域名后边的除去传递的参数外的字符串起作用，

例如 http://www.xy101.com/abc/bbs/index.php?a=1&b=2 只对/abc/bbs/index.php重写。

rewrite跳转实现：
Nginx：通过ngx_http_rewrite_module 模块支持URL重写、支持if条件判断，但不支持else
跳转：从一个 location跳转到另一个location，循环最多可以执行10次，超过后nginx将返回500错误

rewrite 执行顺序如下：

(1) 执行 server 块里面的 rewrite 指令。
(2) 执行 location 匹配。
(3) 执行选定的 location 中的 rewrite 指令。

rewrite的语法格式：

第一种：

rewrite <regex> <replacement> [flag];

regex ：表示正则匹配规则。
replacement ：表示跳转后的内容。
flag ：表示 rewrite 支持的 flag 标记。

第二种：

$request_uri
if ($全局变量 ~ URL路径正则表达式) {
    rewrite  正则表达式  重写的地址  [标记位];
}

flag标记说明：

last ：本条规则匹配完成后，不终止重写后的url匹配，一般用在 server 和 if 中。
break ：本条规则匹配完成即终止，终止重写后的url匹配，一般使用在 location 中。
redirect ：返回302临时重定向，浏览器地址会显示跳转后的URL地址。
permanent ：返回301永久重定向，浏览器地址栏会显示跳转后的URL地址。

案例:

1.将请求http://www.xy101.com/abc/123.html 跳转到首页http://www.xy101.com

location /abc/123.html {
    root /var/www/html
    rewrite ^/ http://www.xy101.com;
}

2.将请求http://www.xy101.com/abc/test.jpg 跳转到http://www.xy101.com/error.png

location /abc/test.jpg {
    root    /var/www/html;
    rewrite ^/ error.png permanent;  
    }

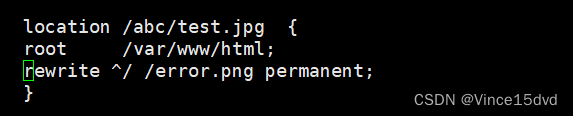3.将请求http://www.xy102.com/discuz/index.php 跳转到http://www.xy101.com/discuz/index.php ，保证原域名后面的uri路径不变

if ($host = 'www.xy102.com') {
   rewrite ^/(.*)$ http://www.xy101.com/$1 permanent;
   }

4.将请求http://discuz.xy101.com/index.php 的访问跳转到http://www.xy101.com/discuz/index.php ，保证原域名后面的uri路径不变。

if ($host = discuz.xy101.com){
    rewrite ^/(.*)$ http://www.xy101.com/discuz/$1 permanent;
   }

5.将对http://www.xy101.com 网站的所有请求跳转到自定义的维护页面或图片，本地可以访问

set $rewrite ture;
if ($remote_addr = "本地主机主机ip") {
   set rewirte false;
}

if (rewrite = true) {
    rewrite ^/weihu.html;
} 

location = /weihu.html {
   root /var/www/html;
}