1.分布式锁Redisson
简单介绍:
使用setnx可能会出现的极端问题:

Redisson的简介:

简单的使用:
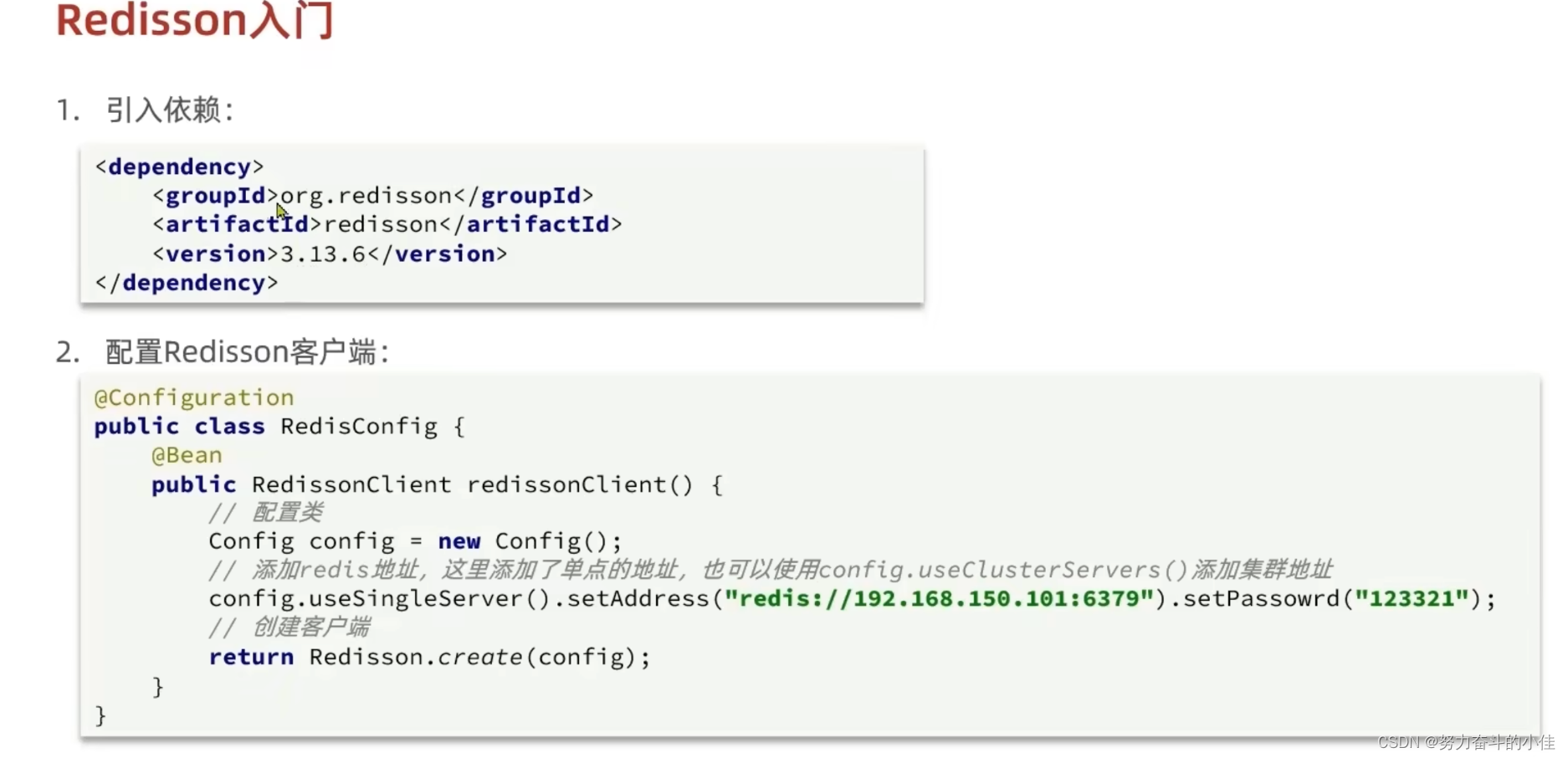
 业务代码的改造:
业务代码的改造:
private void handleVoucherOrder(VoucherOrder voucherOrder) {
Long userId = voucherOrder.getUserId();
//创建锁对象(兜底)
RLock lock = redissonClient.getLock("lock:order:" + userId);
//获取锁
boolean isLock = lock.tryLock();
//判断是否获取锁成功
if (!isLock) {
//获取失败,返回错误或者重试
throw new RuntimeException("发送未知错误");
}
try {
voucherOrderService.createVoucherOrder(voucherOrder);
} finally {
//释放锁
lock.unlock();
}
}