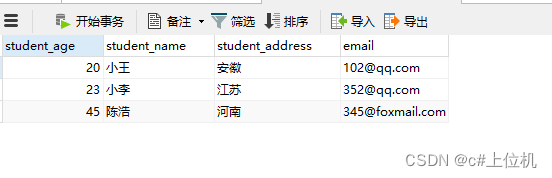
题目（leecode T654）：

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

1. 创建一个根节点，其值为 nums 中的最大值。
2. 递归地在最大值 左边 的 子数组前缀上 构建左子树。
3. 递归地在最大值 右边 的 子数组后缀上 构建右子树。

返回 nums 构建的 最大二叉树 。

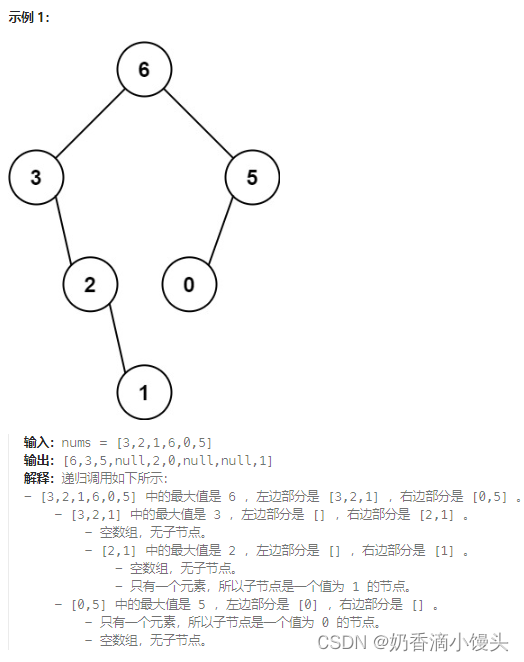
方法：本题可以看出是按照同一个处理原则的重复处理，因此还是用递归法比较方便。确定三要素

1：传入参数和返回值，因为给定的是一个数组。所以我们传入的参数就是数组，而我们要返回的是一个构造好的树，因此返回值是存储树节点的指针

2：确定终止条件，因为题目中已经表示数组不会为空，因此当数组元素只剩一个时，代表该元素是树的叶子节点，到这里就可以结束了。

3：确定单层的处理逻辑，每一层中我们要处理的是，我们要找到当数组中最大的元素，用该元素来构造根节点，然后该元素左半部分继续递归生成左子树，右半部分继续递归生成右子树。

题解：
 

class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        TreeNode* node = new TreeNode(0);
        if(nums.size() == 1){
            node -> val = nums[0];
            return node;
        }
        int maxValue = 0;                                //找数组最大的元素当根节点
        int maxValueIndex = 0;
        for(int i = 0; i < nums.size(); i++){
            if(nums[i] > maxValue){
                maxValue = nums[i];
                maxValueIndex = i;
            }
        }
        node->val = maxValue;
        if(maxValueIndex > 0){                           //切分左子树
            vector<int> newVec(nums.begin(), nums.begin() + maxValueIndex);
            node -> left = constructMaximumBinaryTree(newVec);  //递归生成左子树
        }
        if(maxValueIndex < (nums.size() - 1)){           //切分右子树
            vector<int> newVec(nums.begin() + maxValueIndex + 1, nums.end());
            node ->right = constructMaximumBinaryTree(newVec);  //递归生成右子树
        }
        return node;
    }
};